

降压转换器拓扑结构简析2
描述
降压转换器2
今天继续分享介绍降压转换器的一些知识。先来首歌静下心哈哈。
图1显示了降压转换器的基本拓扑结构。Q1开关以固定频率和可变占空比信号运行。
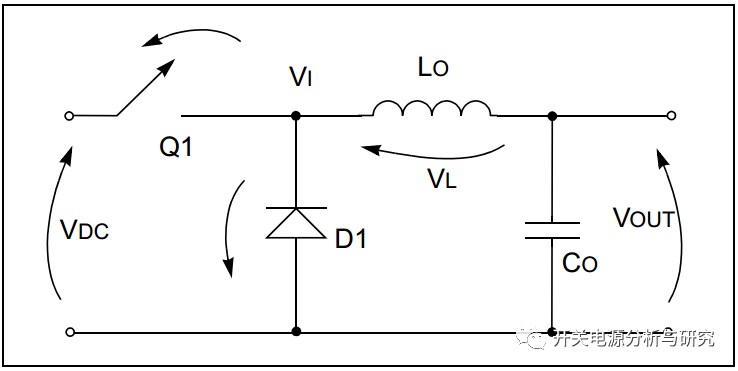
图1:降压转换器拓扑
Q1导通(TON)
在这种配置中,电路重新绘制,如图2所示。二极管反向偏置,使其成为开路。
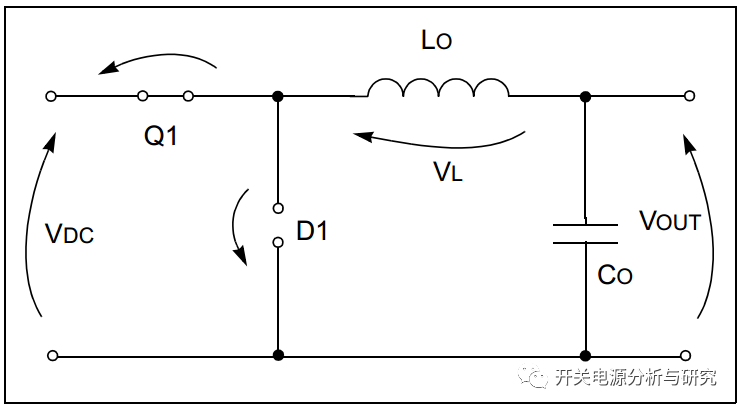
图2:降压转换器拓扑:TON
根据图2,电感上的电压如公式1所示。
公式1:

Q1断开(TOFF)
如图3所示,当开关Q1打开时,电感器将尝试保持电流像以前一样流动。
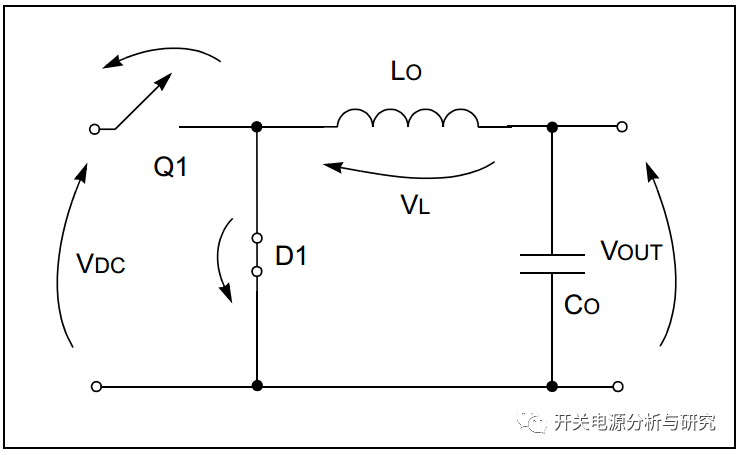
图3:降压转换器拓扑:TOFF
结果,D1,LO,Q1交叉点处(即通常所说的“SW”点)的电压将突然变为负,以支持在相同方向上的连续电流。公式2显示了此时的电感电压,而公式3显示了电流。
公式2:
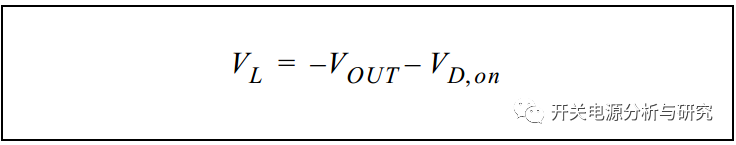
公式3:
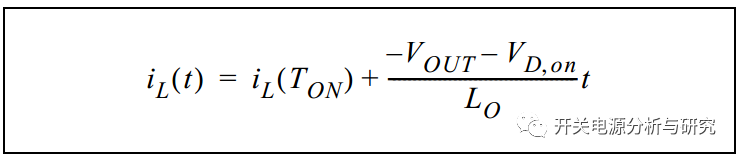
输入/输出关系和占空比
到目前为止所描述的被称为连续模式。要了解它的含义及其重要性,请参考图4(G),它代表电感电流。如前所述,电感电流在TON期间上升,在TOFF期间下降。
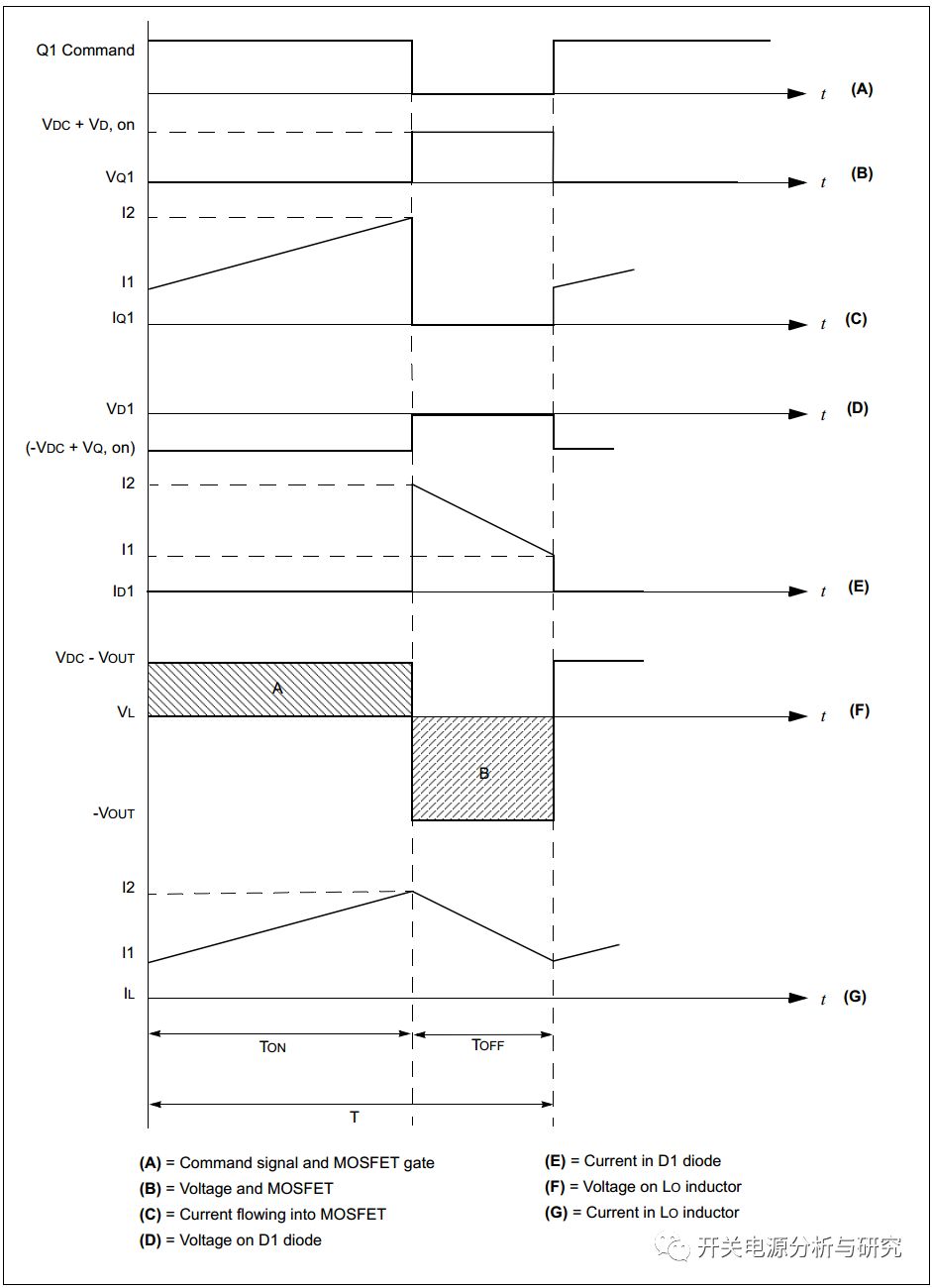
图4:降压转换器波形
可以使用公式4轻松计算平均电流。
公式4:
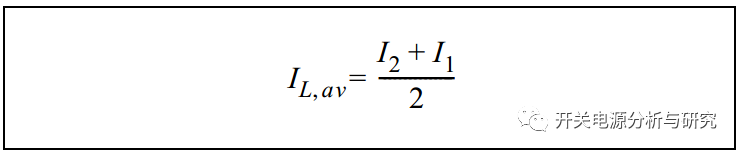
平均电感电流也就是流向输出的电流,因此输出平均电流等于公式5。
公式5:
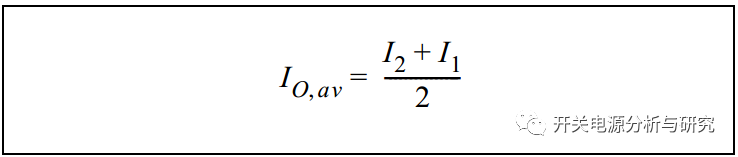
当输出负载RO(与输出电容器CO并联连接)的值增加,这样会降低平均输出电流。如图5所示,电流从标称负载的A线移动到较大负载的B线。应该注意的是,在TON和TOFF期间,两个斜坡的斜率不会改变,因为它们仅依赖于VDC,VOUT和L,并且这些值没有被改变。由于VO等于常数(控制回路处理这个)所以RO增加,电流会减小。
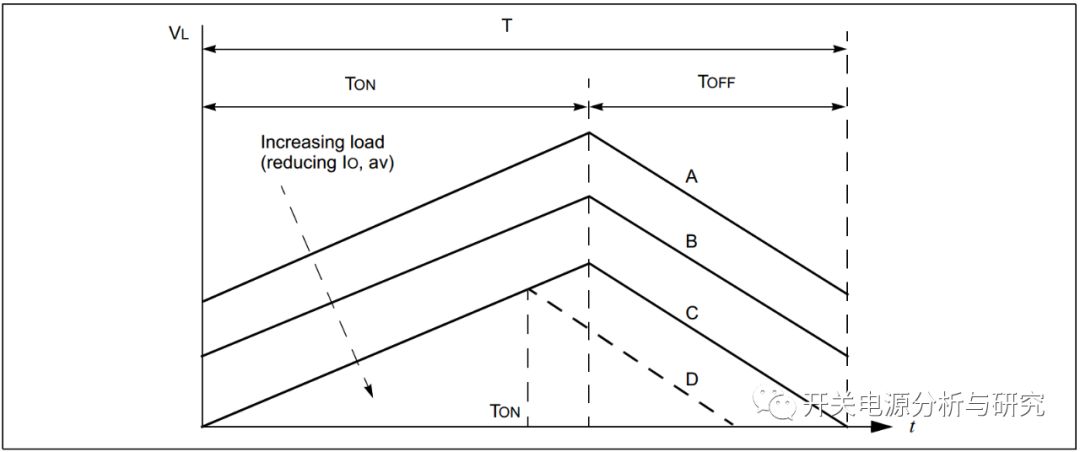
图5:不同负载下的电感电流
连续模式
连续模式的命名是源自于电感中的电流永不停止流动(变为零)。
如图5所示,如果负载继续增加(减小IO,av),则在某个时间电感器电流图将接触x轴(线C)。这意味着电感器中的初始和最终电流(在开关周期的开始和结束时)为零。此时,电感电流被认为是进入了临界模式。
如果负载进一步增加,则下降斜坡期间的电流将在周期T(线D)结束之前达到零,这被称为不连续模式。
一个关键点是TOFF周期结束时的电感电流必须等于TON周期开始时的电感电流,这意味着一个周期内电流的净变化必须为零。当所有瞬态完成且电路行为不再变化时,这必须在稳态下成立。
使用从等式1和等式3导出的IL(TON)的值产生等式6中所示的关系。
公式6:
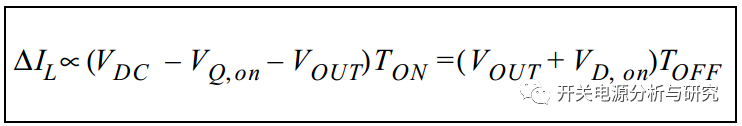
忽略VD,on和VQ,on,可以求解VOUT的公式6,如公式7所示。
公式7:
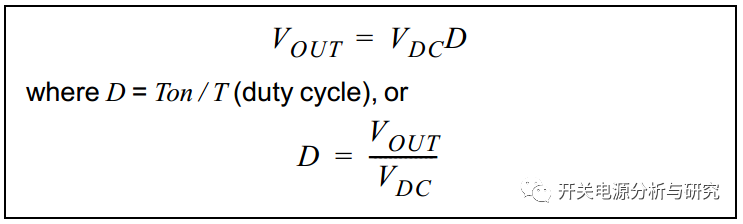
当输入电压处于最小值时,实现最大占空比,如公式8所示。
公式8:
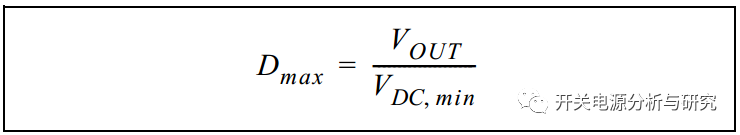
D明显在'0'和'1'之间。
非连续模式
在非连续模式下,电感电流在周期T结束前变为零。决定连续和非连续模式之间边缘的电感(输出)平均电流(IO,av,min)可以很容易地确定,如图6所示。
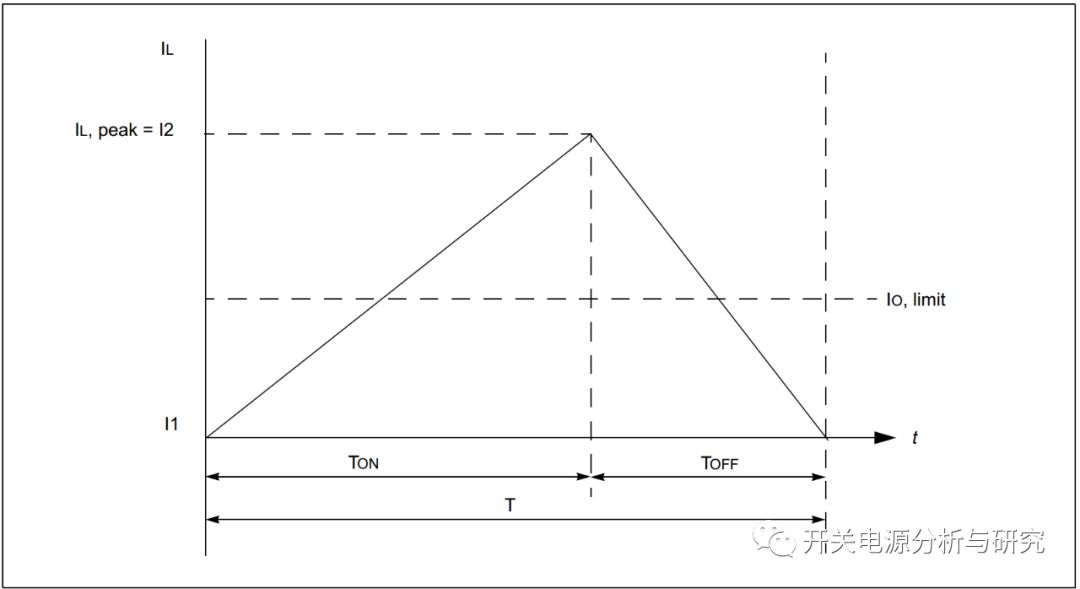
图6:非连续模式边缘的电感电流
根据图6,电感电流限制等于公式9。
公式9:
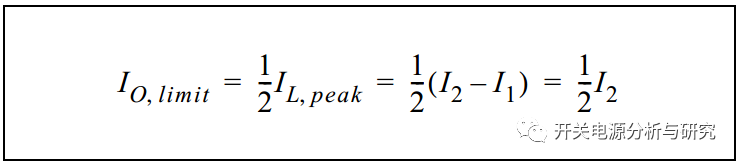
从这一点开始,降压转换器的行为会发生根本性的变化。如果负载继续增加,系统必须降低电流的唯一可能性是减少占空比(图5)。但是,这意味着输入和输出之间不再存在如公式9所示的线性关系。
VDC,VOUT和D之间的关系可以通过一些额外的推导获得,如公式10所示。
公式10:
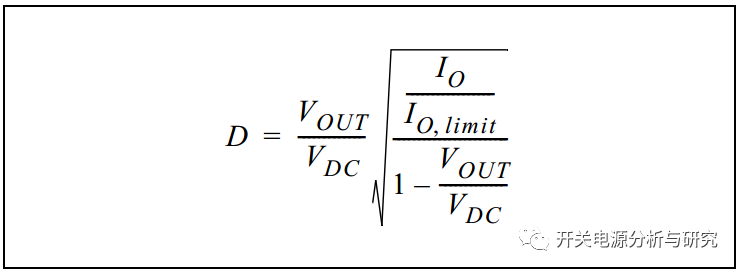
图7说明了这种关系。
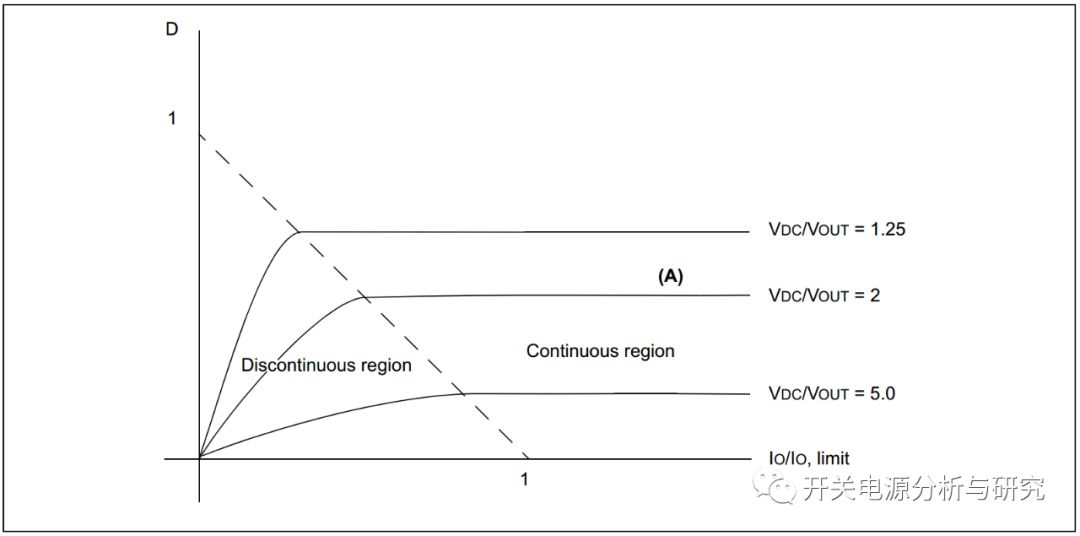
图7:连续和非连续区域的占空比
如图7所示,从连续区域开始沿着线(A)移动,在跨过虚线之前这段距离内,D=0.5,保持相同的输出电压(VDC/VOUT)=2,从连续区域(虚线)之间的边界越过后D根据等式10中的非线性关系而变化。
-
降压-升压转换器2023-11-24 1658
-
升-降压型DC-DC的工作原理和拓扑结构2023-06-06 14137
-
基于降压转换器拓扑结构实现双极性电源设计2022-03-24 1476
-
深入介绍降压、升压和降压-升压拓扑结构2021-12-31 2793
-
使用三种方法详细说明降压和升压及降压升压拓扑结构2021-02-15 8890
-
非反向降压-升压转换器的拓扑结构和如何实现应用设计2020-08-30 2795
-
降压转换器拓扑结构简析12019-07-16 6462
-
降压、升压和降压升压拓扑结构详解2019-03-19 4205
-
基于串联谐振拓扑结构的正弦振幅转换器2019-03-18 5910
-
采用4开关降压-升压转换器的USB供电设计2018-10-30 2676
-
汽车系统中设计降压或升压转换器2018-07-09 3780
-
基于ZETA拓扑结构的DC/DC转换器设计2012-05-07 4544
全部0条评论

快来发表一下你的评论吧 !

