FFT、PFT和多相位DFT滤波器组瞬态响应的比较

摘要：本文简要地论述了FFT和多相位DFT滤波器组在响应方面的差异。一般而言，多相位DFT(甚至包括任何滤波器组，比如PFT)在稳态条件下有着很好的相邻信道抑制性能，而瞬态响应却很糟糕。这符合了滤波器冲激响应结论。通过对一个典型的1024子带滤波器组研究的简单例子说明这些不同点。

引言
滤波器组频率响应的研究是一个非常复杂的课题。这方面的大多数文章只研究稳定状态下的响应，事实上，雷达和其它突发方式的信号具有瞬时的特性。因此，了解滤波器组的瞬时性能是非常重要的。一般而言，频率分辨特性越好，稳定下来需要的时间越长。这是因为越是陡峭的滤波器，其需要的抽头就越多、冲激响应时间越长。因此，在稳定期间，滤波器抽头没有充满，相邻信道的频率响应实际上比非加权的FFT滤波器组还要差。
本文将对FFT和多相位DFT滤波器组进行比较，包括稳定状态和瞬时条件的情况。同时也简要地分析了过抽样和所谓的“最小相位”滤波器的内容。

滤波器组稳定状态下的
频率响应
频率响应的比较
众所周知，管道FFT的有效滤波器响应是Sinx/x (Sinc)函数，对很多应用，它不能提供足够的相邻信道抑制能力。使用简单的窗口函数，比如Hanning, Kaiser, Blackman-Harris等，可改善滤波器的旁瓣抑制，代价是主瓣宽度减小。通过设计适当的滤波器组，比如PFT和多相位DFT,可以改善频率响应特性。
有效噪声带宽
滤波器性能的另一个重要参数是有效噪声带宽(ENB)。表1给出了几种滤波器组的比较。
由表1可知，Blackman-Harris窗口加权的FFT具有很好的旁瓣抑制，但在信噪比(S/N)上损失超过3dB ；而一个8抽头多相位DFT(如下面要说明的一个8倍变换长度的窗口)具有良好的旁瓣抑制和低的有效噪声带宽，信噪比损失只有1dB 。

图1   2倍过抽样、非加权、1024子带管道FFT瞬态响应

图2   2倍过抽样、5抽头、1024子带多相位DFT瞬态响应

图3  32倍过抽样、5抽头、1024子带多相位DFT瞬态响应

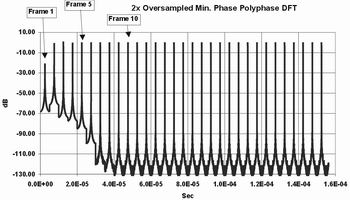
图4  2倍过抽样、5抽头、最小相位、1024子带多相位DFT瞬态响应

一般时域考虑
时域抽样窗口
对简单的窗口抽样，窗口中的抽样点数目等于它自身的变换长度。为了获得更好的滤波效果，需要使窗口中的抽样点数目大于变换长度。理论上，窗口的大小可以为任意长度。在多相位DFT当中，它通常是变换长度的整数倍(2x，3x等)，但是在WOLA实现中，它可以是任意长度。比方说，一个1024子带的滤波器组可能需要4096个输入抽样(4倍帧长度)作为第一个全输出的帧。对于PFT滤波器组，需要的抽样点数目等同于级联滤波器的冲激响应，但实际效果类似于获得第一个全输出帧需要的抽样点数目，远超过了帧的长度。
过抽样
影响处理吞吐量速率的另一个因素是输出滤波器需要的过抽样程度。即使获得临界抽样(抽样速率正好等于奈奎斯特速率)也需要交迭处理。使用上面的例子，形成1024子带的第一个全输出帧需要4096个抽样。要实现临界抽样就意味着1024子带的下一帧在时间上必须与前一帧相邻，并且输出抽样速率必须等于输入抽样速率。这可以通过下一组4096个抽样点的起始延时1024个抽样点、并进行4次交迭处理来实现。要实现过抽样，需要增加交迭的次数。再用以上的例子，2倍的过抽样将需要4096个抽样的延时，而通过8次交迭处理，仅需512个抽样即可满足上述要求。PFT通常采用2倍的过抽样。
过抽样的程度由新抽样的数目M(每一次新变换的参数)决定。M的值越小，过抽样因子越大。

瞬态分析
一般参数
尽管多相位、WOLA 或 PFT滤波器组在稳态条件(如稳定的信号条件和所有的滤波器抽头充满)给出了很好的相邻信道抑制性能，瞬态响应却是另外一种情况。在以下的讨论中，使用的一般参数是：
?子带的数目 = 1024
?输入抽样速率=102.4 MS/s(复数)
?输出抽样速率 = 204.8 MS/s (2倍过抽样)
?多相位抽头的数目=5(等同5120点窗口)
?滤波器阻带抑制 = -85 dB
?滤波器通带纹波 = 0.2 dB(峰—峰)
?滤波器交迭 = 75%
最后一个参数用来测量滤波器的截止率。滤波器被设计成子带的边缘内都是平坦的，然后进入阻带，与相邻子带的宽度有75%的交迭。
瞬态的结果由一个正弦波输入的阶梯函数产生，频率范围从中心频率到半个子带的偏移。它给出了对于FFT的最差的频谱泄漏。
下面将介绍归一化的功率谱(10*Log10{I2+Q2})，描述在2倍过抽样速率(在这种情况下速率是204.8MS/s)情况下的管道输出。一个单独的1024抽样的帧包含了从蠪s/2 到 +Fs/2的交织频率子带，这里Fs是输入复数抽样速率。
FFT瞬态响应
图1给出了非加权FFT的瞬态响应。图中没有表示在第一次输出前需要采集1024个抽样和实际硬件处理带来的任何其它延时的“废弃”时间。因为它是2倍过抽样，第一个1024点的帧还没有达到稳定状态。这可以由以下的事实说明：第一个输出帧在5ms内产生(1024个点以204.8MS/s 的抽样速率产生)，而输入抽样速率是102.4MS/s ，这意味着只有512个抽样是有用的(剩余的为0)。
多相位DFT瞬态响应
图2给出了5抽头多相位DFT的瞬态响应。很显然，与FFT相比瞬态响应的时间要长，并且直到第10帧才完全达到稳定状态。直到第5帧，有效的滤波器频率响应还不如非加权的FFT好。这是因为滤波器的抽头只是半充满。达到全稳定状态花费了10帧的时间(5抽头乘以过抽样因子)。
过抽样的影响
有人可能认为通过在滤波器组的输出端进行过抽样能够减少瞬态响应时间，这是不正确的。瞬态响应是滤波器冲激响应函数，过抽样的影响只是使瞬态响应的细节更加清楚。这可以通过以下的例子说明：
?子带的数目=1024
?输入抽样速率=6.4MS/s (复数)
?输出抽样速率 = 204.8MS/s (32倍过抽样)
?多相位抽头的数目=5(同上具有相同的有效滤波)
图3给出了32倍过抽样的瞬态响应。为了保持204.8MS/s的输出抽样速率(受限于设备最大输出速率)，输入速率必须减小到6.4MS/s。
32倍过抽样情形下的第80和第160帧的瞬态响应恰好对应于2倍过抽样情形的第5和第10帧。这清楚地说明过抽样并没有获得时间上的好处。32倍过抽样的第1帧甚至比2倍过抽样的第1帧还要差，因为现在5120个抽样中只有32个可用。通过将图2和图3进行比较，瞬态响应的细微差别就更加清楚了(注意，由于输入抽样速率从102.4MS/s到6.4 MS/s的改变，引起时间轴刻度不同)。
最小相位FIR滤波器的影响
在此方面，一个更准确的命名是“最小群时延滤波器”，因为对于IIR滤波器而言，通过非线性相位响应的代价，可以减少中心频带的群时延。典型的例子如图4所示。
除了滤波器抽头系数不同，其它参数和图2一样。可以看到，滤波器的幅度响应增长很快，但这并不意味着滤波器在相邻信道抑制方面能够更快的稳定下来。
在最小相位第5帧，尽管幅度已经达到了最大值，但频谱响应还没有达到第9或第10帧的稳定状态条件。这方面的影响与标准多相位DFT的情况是类似的。

结语
结论很清楚。快速瞬态响应和陡峭频谱滤波器不能同时获得。最快速稳定时间可以从简单的FFT(加权或非加权)得到，代价是相对差的频谱滤波特性。从另一个方面看，Sinx/x  FFT 滤波器的阶梯响应很接近立即阶梯响应。
提到“砖墙”滤波器，设计人员必须接受随之引起的由于滤波器需要充满带来的瞬态响应延时。滤波器越陡峭，瞬态时间越长。如果优先考虑给定子带的信号幅度，那么“最小相位”滤波器会有所帮助，但这并不能改善(实际上可能会恶化)瞬态期间的相邻信道抑制性能。这也会带来每一个子带的非线性相位响应。
过抽样在瞬态期间展示更多细节方面有一定的作用，但它不会缩短瞬态响应时间。