超构材料与电磁参量调控

超构材料是由亚波长单元（天线）周期或非周期地排列而组成的人工结构，阵列中每个天线的几何结构以及整个阵列的排布方式都可以进行人工设计，因此超构材料具有极大的设计自由度。经过专门设计的超构材料，可以将滤光片、偏振片和透镜的功能集于一体，实现多功能的电磁参量调控元件。

基于导模谐振光栅的滤光/偏振元件

平板介质光波导是由一层折射率较高的介质材料夹在上下两层折射率较低的介质材料之间而构成的平板导波结构，如图6所示。其中，折射率较高的材料为芯层(n1)，而折射率较低的材料(n2)为包层。借助芯层上下表面处的全反射，光频电磁波可以被有效地局限在芯层中传播，即平板光波导的导模。如果将导模传播的方向规定为z轴，垂直于导模传播方向的截面规定为x-y平面，则导模在z轴方向为行波(传导)，而在x-y平面内则为驻波 (局限)。

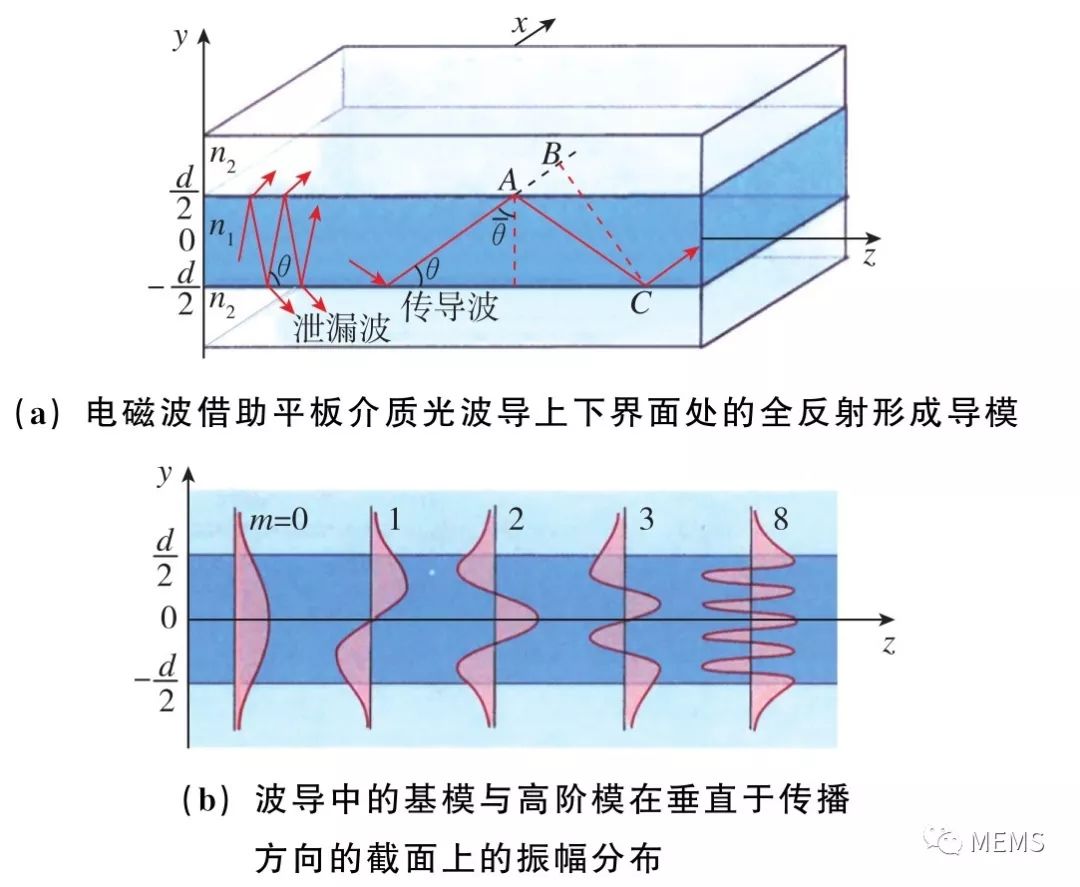
图6 平板介质光波导

如果在平板光波导的表面引入亚波长光栅结构，就可以在某些特定的条件下实现自由空间电磁波与导模的耦合。这些特定的条件也被称为谐振条件，它们实际上是一组 “波长+偏振态+入射角”的电磁参量组合，而整个 “亚波长光栅+平板光波导”的结构也因此被称为导模谐振光栅，如图7所示。导模谐振光栅对自由空间电磁波的透射和反射，天然地具有波长选择性和偏振选择性，而这种波长选择性和偏振选择性可以通过结构设计来实现灵活调控。因此，导模谐振光栅可被用作多功能的滤光/偏振元件。需要指出的是，导模谐振光栅存在两种极端情况：当光栅层厚度为0时，整个结构退化为介质平板波导；而如果波导层的厚度为0，则整个结构演变为单纯的亚波长光栅。因此在这里，将介质平板波导和亚波长光栅都归入导模谐振光栅的类别。图7(a)展示了一种波导层厚度为0的导模谐振光栅，光栅的周期性结构单元由硒和锗两种材料组成，衬底为二氧化硅。通过优化设计结构参数，该导模谐振光栅可以作为中红外波段的透射式窄带滤光片使用，如图7(b)所示。图7(c)展示了一种硅基导模谐振光栅，该光栅可以通过在硅薄膜中刻蚀出周期性纳米硅柱阵列而获得。如图7(d)所示，通过改变波导层厚度，可以灵活调控光栅的反射谱。图7(e)和图7(f)分别显示了该硅基导模谐振光栅在波导层厚度为0和不为0时的典型光场模式。这种光场模式，可被看作是振幅受到光栅结构调制的行波，即布洛赫波。

 

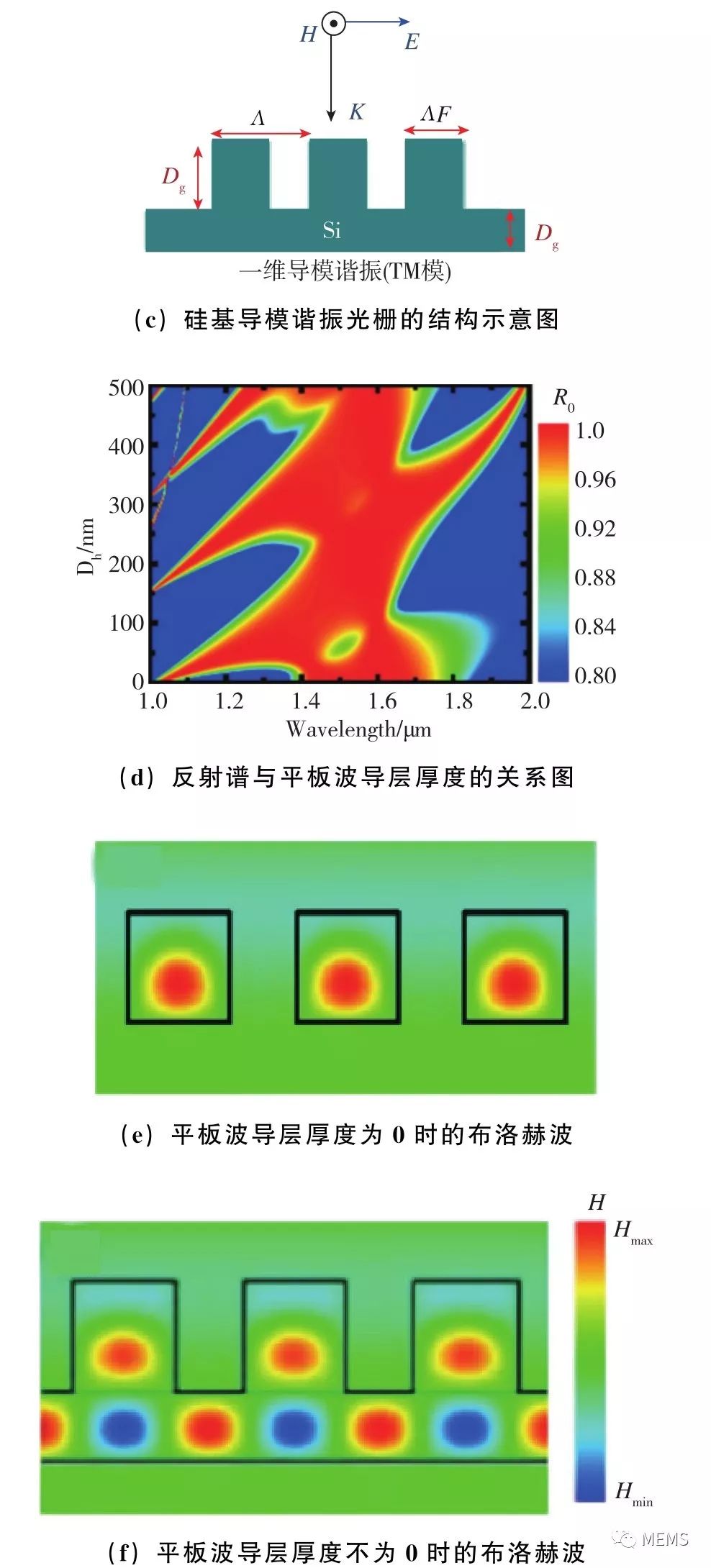
图7 导模谐振光栅

2.2 基于超构材料吸收体的滤光/偏振元件

另外一类具有代表性的滤光/偏振元件，是基于超构材料的电磁波吸收体。顾名思义，超构材料吸收体既不透射电磁波，也不反射电磁波，而是吸收电磁波。为了实现对电磁波的高吸收率，超构材料吸收体往往由金属或重掺杂的半导体等对电磁波有较大损耗的材料构成的亚波长单元(天线)阵列组成。在光频电磁波的激励下，天线表面的自由电子产生共振，即局域表面等离激元共振（LSPR）。从等效电路的角度来看，共振的自由电子对应于天线等效电路中的谐振电流源；天线的结构和尺寸，决定了等效电路中的电感项和电容项，以及相应的谐振频率；而天线材料的电导率总是有限的，这使得等效电路中总存在一个欧姆电阻项。因此，天线对电磁波的吸收，来源于谐振电流在天线中产生的欧姆损耗，如图8所示。

 

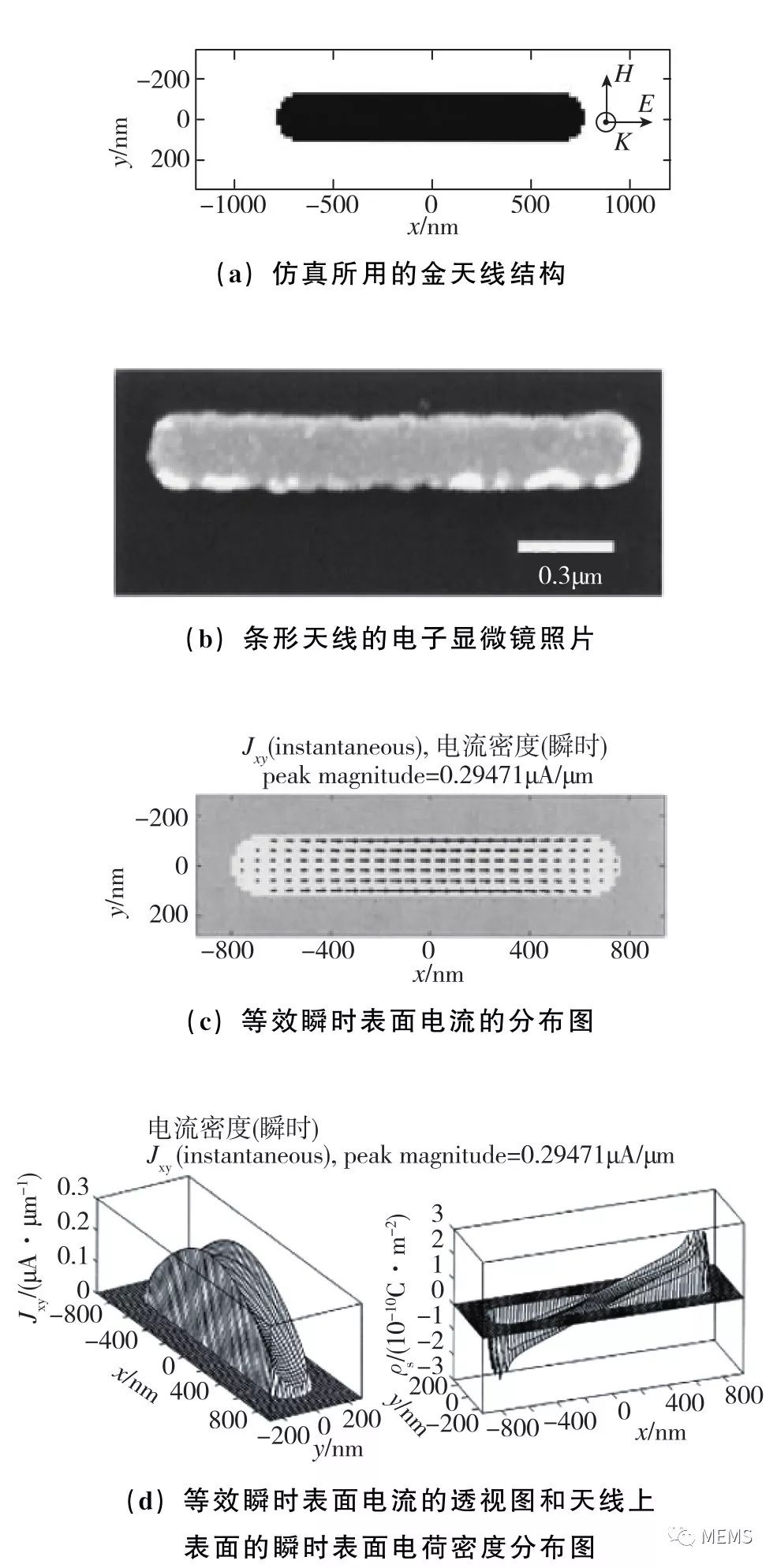
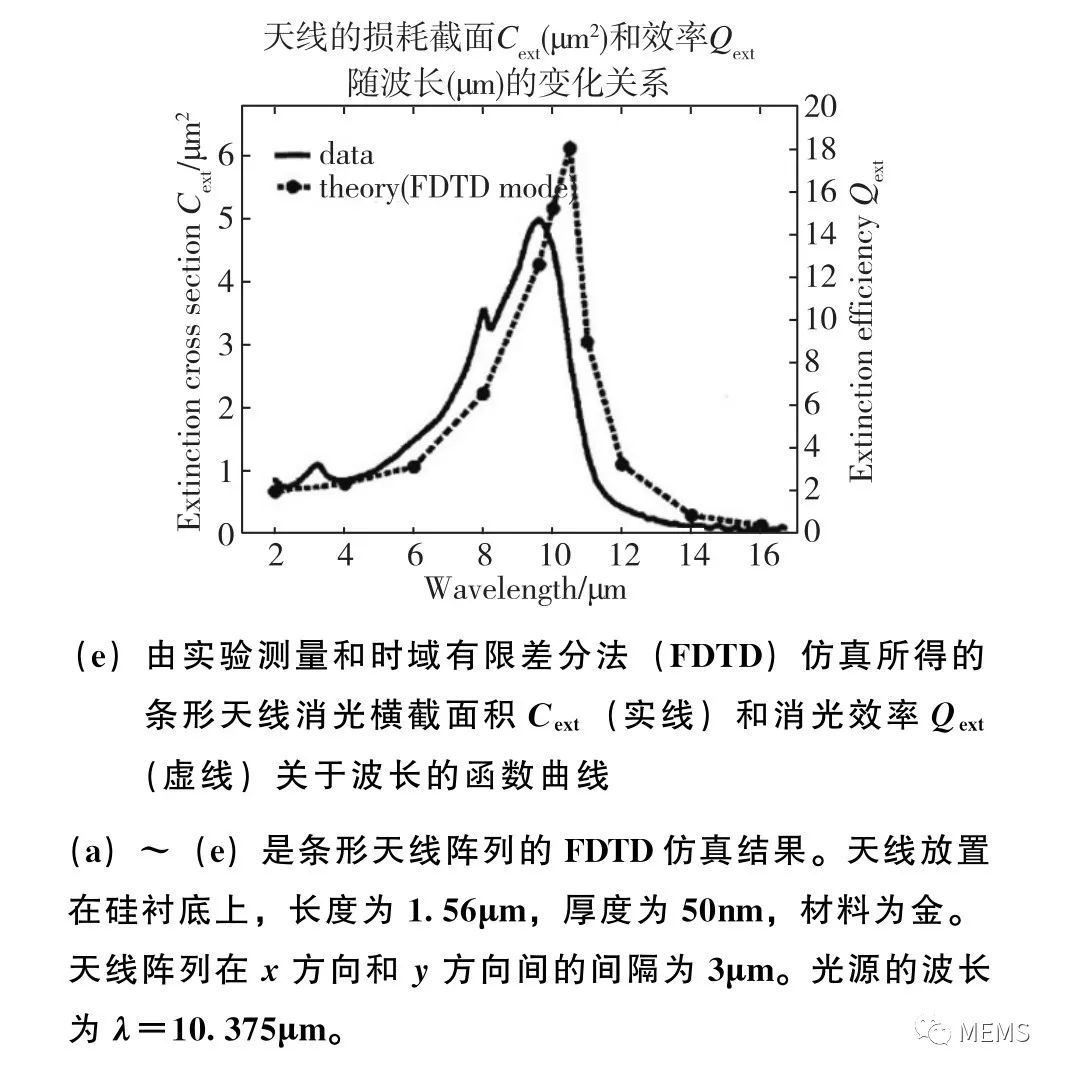
图8 金属光学天线在电磁波激励下产生的电流与欧姆损耗

单层天线阵列，虽然能够吸收一部分入射电磁波，但仍然会透射和反射部分电磁波。为了实现对电磁波的完美吸收，可以采用 “金属-介质-金属”的三层结构：其中的上金属层是天线阵列，中间的介质层用于调控上下金属层之间的距离，而下金属层保持连续，且厚度足够，能完全阻挡电磁波的透过，如图9所示。当电磁波从天线阵列一侧射向三层结构时，不仅会激励起天线表面的自由电子共振(电共振)，而且天线表面的谐振电流还会在下金属层的表面诱导出反相的谐振电流，进而在介质层中激励起磁共振。通过调节天线的大小和介质层的厚度，可以分别调控电共振、磁共振与入射电磁波的耦合强度。在特定的条件下，可以将入射电磁波的能量完全馈入电共振与磁共振，此时电磁波的反射系数为0，以实现电磁波的完美吸收。而这些特定的条件，实质上也是一组 “波长+偏振态+入射角”的电磁参量组合。因此，超构材料吸收体对电磁波的吸收，也具有波长选择性和偏振选择性，可被用作吸收式的多功能滤光/偏振元件。

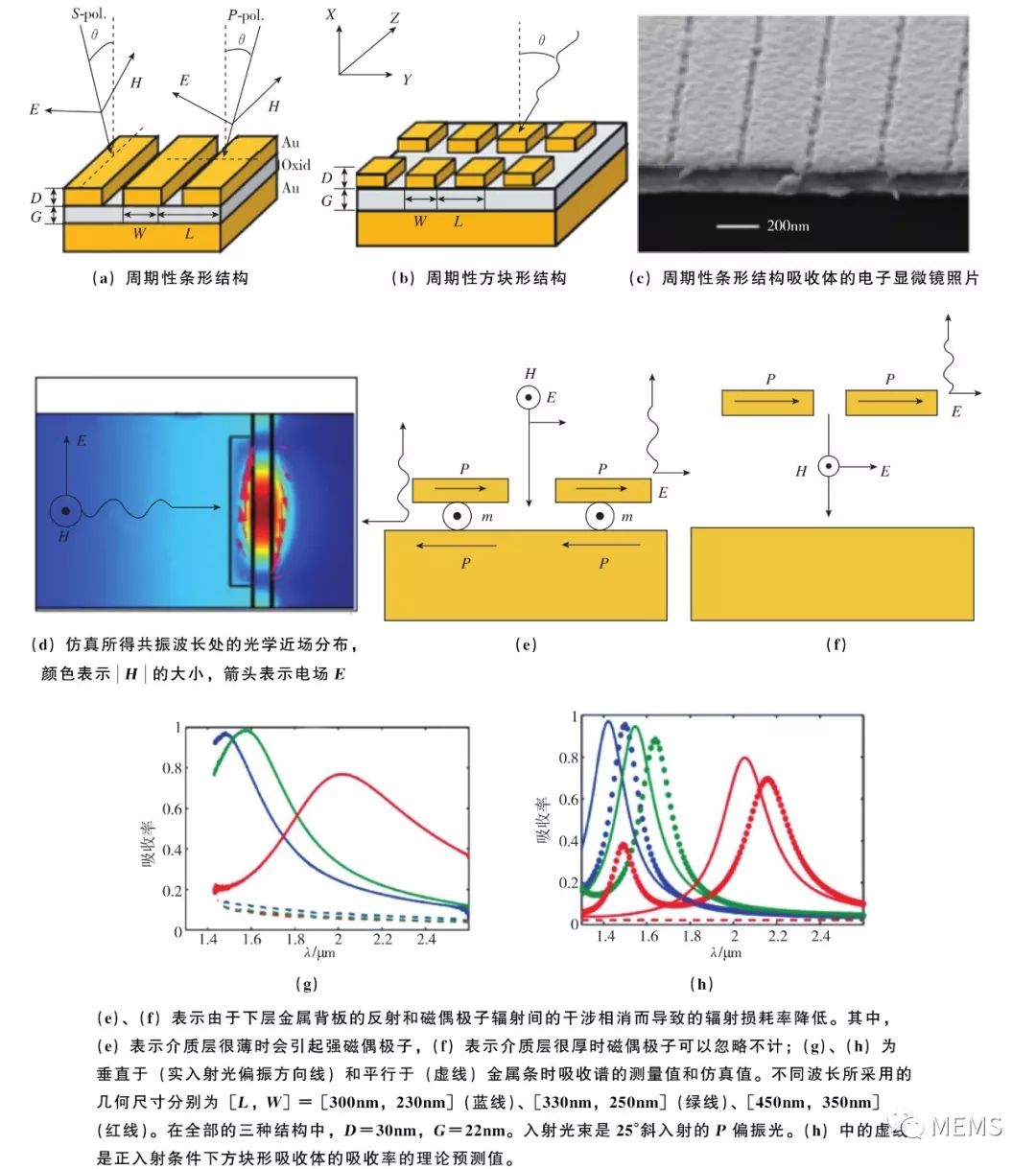
图9 基于 “金属-介质-金属”三层结构的超构材料吸收体

2.3 基于超构材料的波前调控元件

除了调控电磁波的波长和偏振态，天线也可被用于调控电磁波的相位。2011年，美国哈佛大学Capasso课题组在《Science》杂志上发表论文，提出可以利用天线阵列调控电磁波的等相位面，即波前。作者首先分析了在入射电磁波激励下，纳米棒金天线中产生的谐振电流。如图10(a)所示，在电磁波的激励下，纳米棒金天线中的自由电荷产生高频振荡，振荡的自由电荷可等效为谐振电流，而天线则可等效为金属谐振腔，可以用弹簧振子的模型来描述。纳米棒金天线的长度L与其最低阶谐振模式的谐振波长λsp之间的关系是L≈λsp/2n,这里的n是放置天线的衬底材料的折射率。图10(b)示例了一个纳米棒金天线对电磁波的吸收截面（absorption crosssection）、散射截面 （scattering cross-section），以及近场光强（near-field intensity）随入射波的波长λ的变化曲线。可以看出，三者在λ=7μm附近有最大值，即纳米棒金天线的谐振波长λsp≈7μm。图10(b)给出了散射波与入射波之间的相位突变,即天线的相位响应随入射波波长的变化曲线。可以看出，当入射波波长λ等于天线谐振波长λsp时，散射波与入射波的相位突变为-π/2；当λ>λsp时，相位突变趋近于0；而当λ<λsp时，相位突变趋近于-π。也就是说，在谐振波长λsp附近，天线的相位响应存在一个从0到π的快速变化过程。那么，如果将入射波波长设定为λsp，通过改变天线的长度L，也可以实现相位响应从0到π的变化，这也就构成了利用天线阵列调控电磁波的波前(等相位面)的物理基础。

 

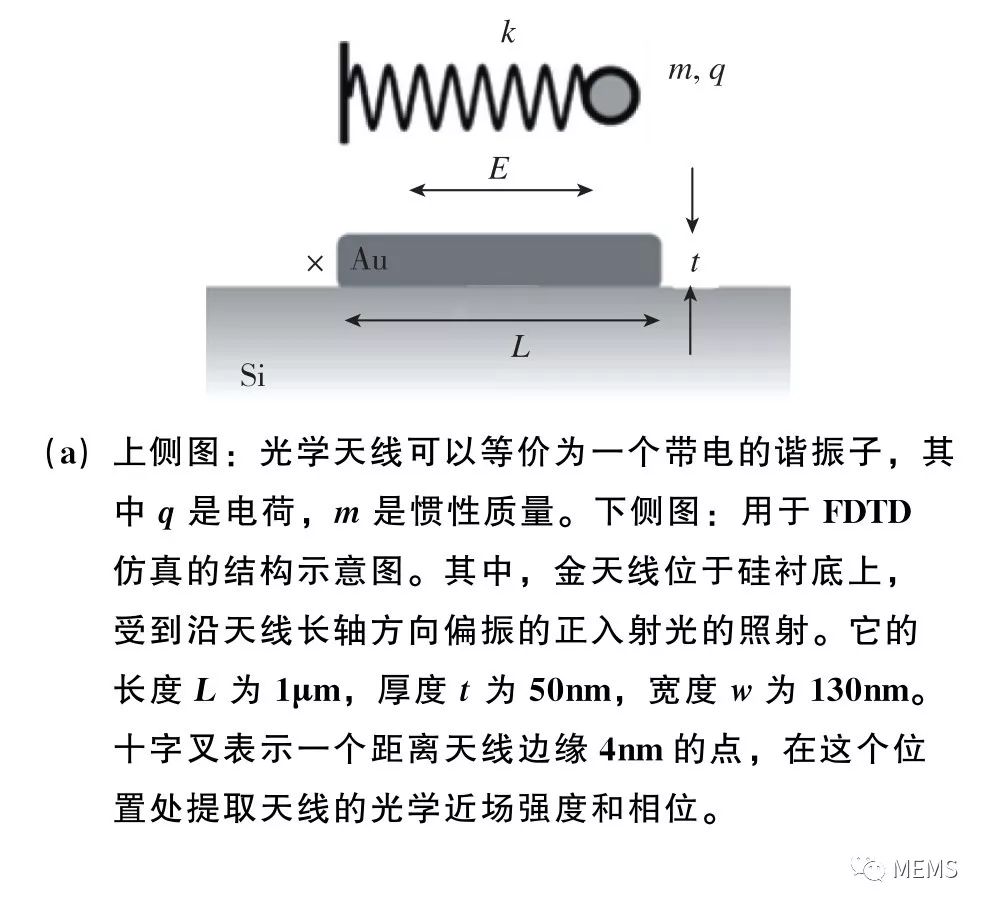
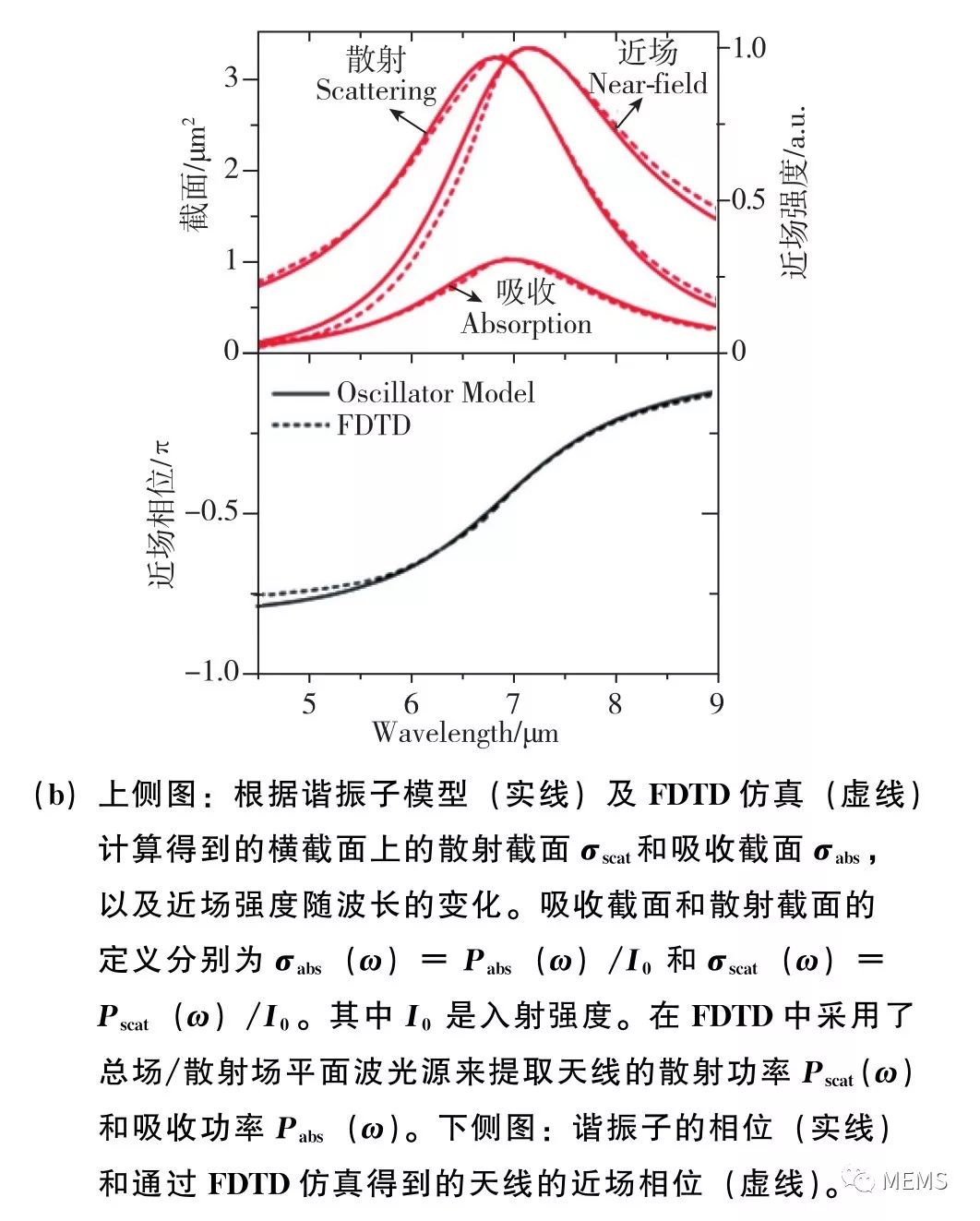
图10 纳米棒金天线的振幅响应与相位响应

纳米棒金天线只能产生0到π的相位突变，不足以覆盖0到2π的完整相位取值范围。为实现对波前的完全操控，Capasso等人提出了V型天线结构，如图11(a)所示。这种V型天线由长度相等的一对纳米棒按一定的夹角在端点处连接而成，夹角的中线为对称轴。当入射电磁波的电场矢量平行于对称轴时，在V型天线中激发起对称的谐振电流(对称模式)；当入射电磁波的电场矢量垂直于对称轴时，在V型天线中激发起反对称的谐振电流(反对称模式)。与纳米棒天线相比，V型天线的结构更复杂，可以改变的参数更多，因此其对电磁波造成的相位突变范围也更大。图11(b)、图11(c)显示了当工作波长λ=8μm时，V型天线的振幅响应和相位响应随臂长h和夹角Δ的变化关系。根据这些关系，可以找出振幅响应相等的8种V型天线结构，它们之间的相位响应依次相差π/4，而这8种天线结构合在一起可以覆盖0到2π的完整相位取值范围。图11(d)则显示了这8种天线结构在同样的入射电磁波激励下产生的散射场，相邻的两种天线结构发出的电磁波的波前传播距离之差为1μm，对应的相位差为π/4。如果将这8种天线结构作为一组基本单元，就可以在两种材料的界面处引入界面内的局部相位梯度dΦ/dx。如图11(e)所示，在引入相位梯度后，电磁波在该界面处的折射过程不再简单服从传统的折射定律(即nt sinθt=nisinθi),而是服从广义折射定律ntsinθt-nisinθi=(1/k0)*(dΦ/dx)。因此,当入射角θi一定时，折射角θt不仅由两种材料的折射率ni和nt决定，还受到界面处引入的相位梯度dΦ/dx的调控；同样，电磁波在该界面处的反射过程，也不再简单服从传统的反射定律(即sinθr=sinθi)，而是服从广义反射定 律sinθr-sinθi=[1/(k0ni)]*(dΦ/dx)。因此，反射角θr不仅由入射角θi决定，还受到相位梯度dΦ/dx的调控。可见，相位梯度dΦ/dx为调控电磁波在界面处的反射与折射提供了新的途径。需要强调的是，以上讨论仅局限于二维情形，即相位只沿x方向存在梯度变化。如图11(f)所示，对于三维的情况，如果在垂直于入射面的方向引入相位梯度的分量dΦ/dy，就可以使折射电磁波和反射电磁波的波矢偏离入射面，这种情况称作异常折射和异常反射。

透镜是典型的电磁波波前调控元件，在各类光学系统中都有广泛的应用。在提出广义折反射定律之后，Capasso等进一步展示了如何设计天线阵列，以获得与传统透镜同样的波前调控功能。图12(a)展示了平面透镜(flat lens)和平面锥镜(flat axicon)对入射波引入的附加相位分布函数。平面透镜引入的附加相位分布由式(1)给出：

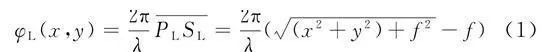
式(1)中，(x,y)为平面透镜或锥镜上的坐标，λ为工作波长，其他量参照图12(a)。图12(b)展示了用于计算V形天线的振幅响应和相位响应的数值仿真设置，以及挑选出来的8种相位响应能覆盖0到2π的V形天线结构。图12(c)展示了一个实验制备的平面透镜的天线阵列细节。图12(d)、图12(e)则展示了对实验制备的平面透镜和平面锥镜进行测量所得到的聚焦效果。

平面锥镜引入的附加相位分布由式(2)给出：

 

 

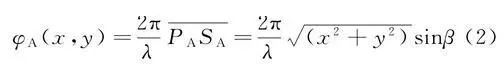
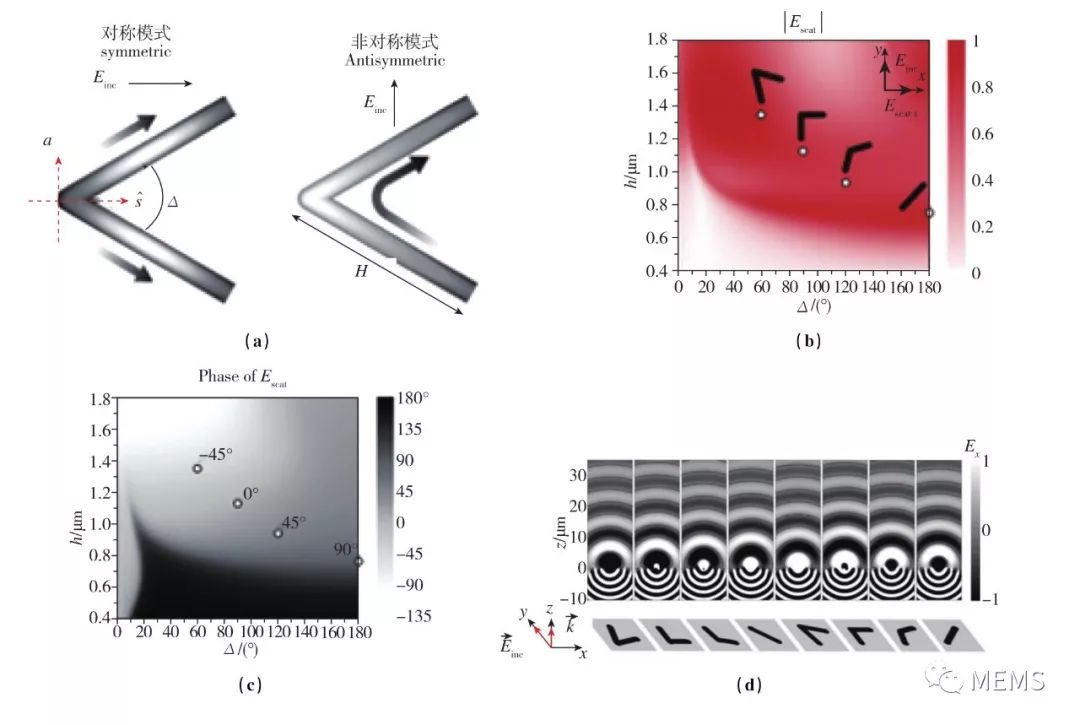
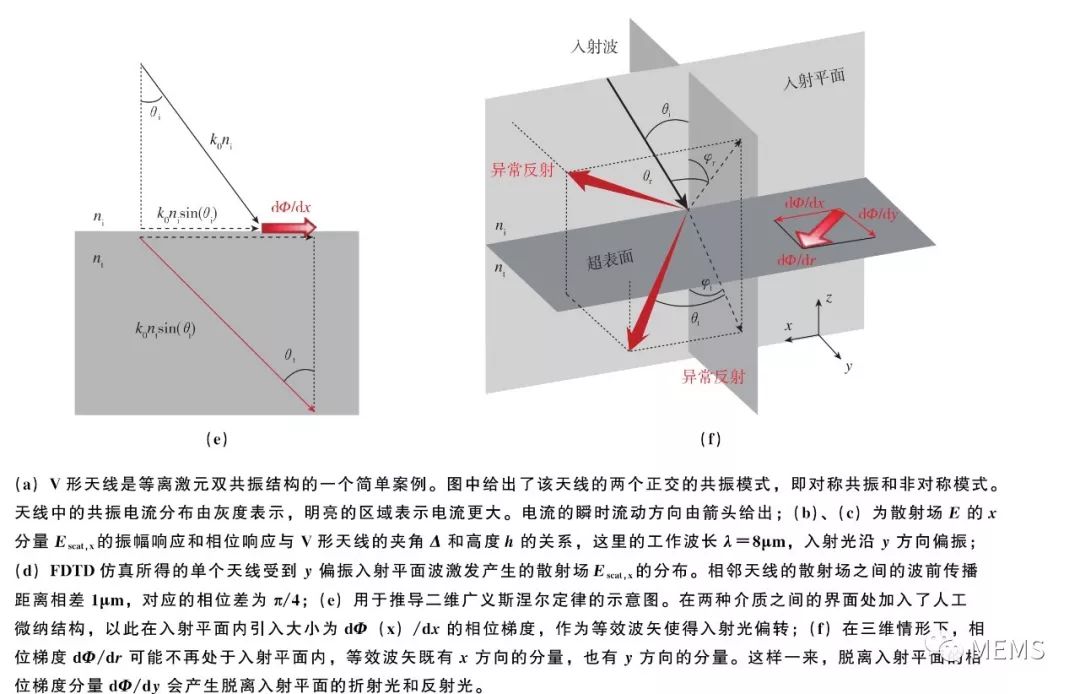
图11 V型金天线的振幅响应与相位响应以及对电磁波前的调控

 

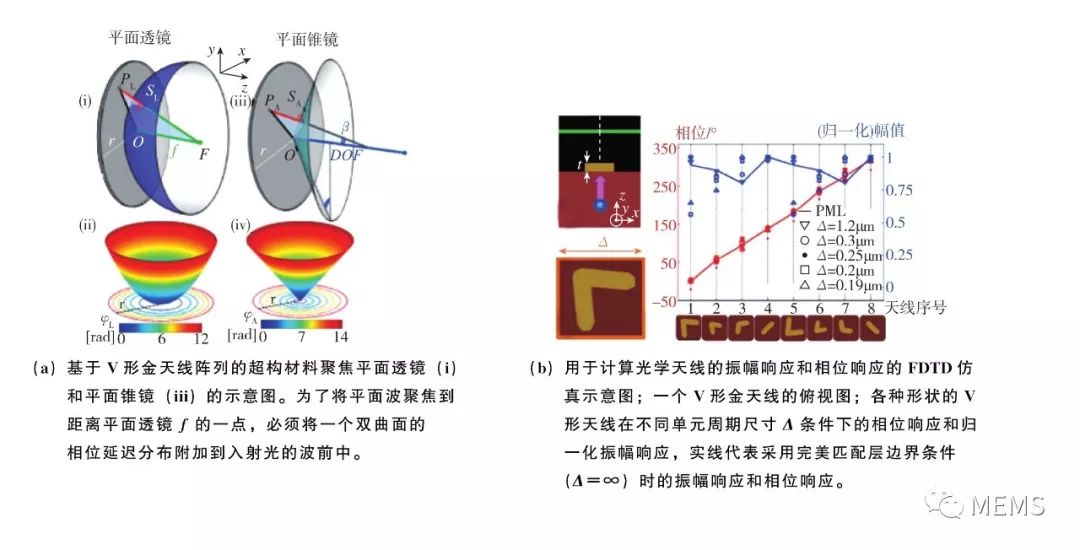
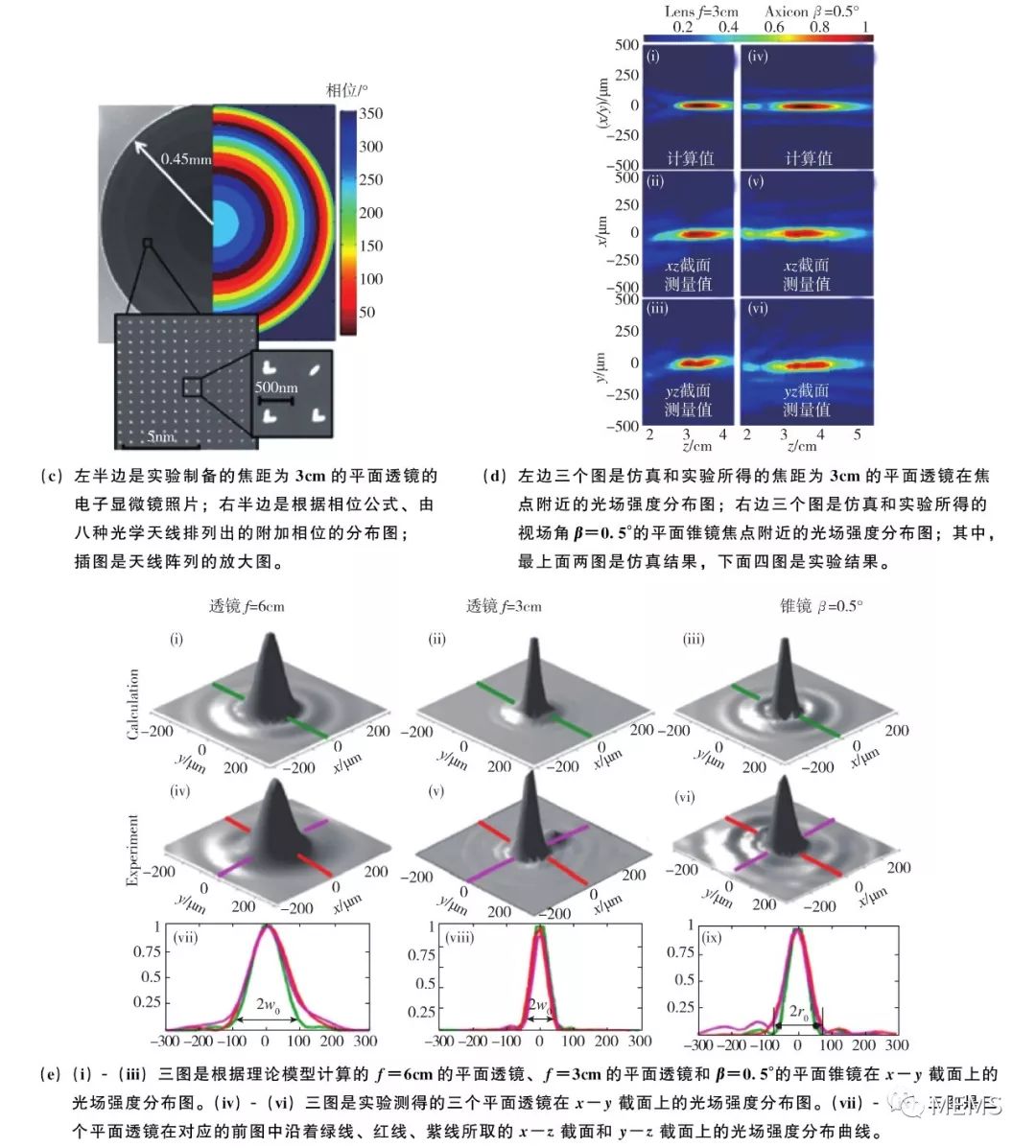
图12 基于V形金天线阵列的聚焦超透镜

 超构材料与红外探测芯片的结合

超构材料具有强大的电磁波参量调控与分辨功能，可以构成多功能的超薄平面光学元件。由于超构材料的制造工艺与集成电路芯片的制造工艺是一致的，而目前集成电路的工艺节点尺寸已达到了10nm以下的精度，因此大规模制备基于超构材料的多功能电磁参量调控元件也不存在根本性的障碍。用超构材料取代单一功能的传统红外光学元件，并与红外探测芯片结合，势必革新传统的红外成像探测系统架构，导致结构更为紧凑、功能更为多样的红外探测成像系统出现，而这也契合了红外探测芯片和成像系统的未来发展趋势：在系统紧凑化、轻量化的基础上实现更多的功能。以下，对近年来国内、外在将超构材料与红外探测芯片结合、压缩成像系统体积并实现新型探测功能方面的代表性工作进行了回顾与梳理。

3.1 超构材料调控探测芯片的光谱响应

日本三菱电子公司高等技术研究所的Shinpei Ogawa等人从2012年开始发表了一系列论文，报道了如何将超构材料吸收体集成在基于掺杂多晶硅的热电堆探测器像元上，实现波长选择型探测和偏振选择型探测。如图13(a)、图13(b)所示，论文采用了圆形金属槽阵列作为具有波长选择功能的超构材料吸收体。从图13(c)可以看出，超构材料吸收体只在某个峰值波长附近较窄的波长范围内具有高吸收率，而通过调节金属槽阵列的单元周期，可以调控峰值吸收波长。因此，超构材料吸收体起到了波长可调的吸收式窄带滤光片的作用。如果将超构材料吸收体与热电堆探测器的像元进行集成，如图13(d)、图13(e)所示，就可以实现波长可调的窄带热探测。需要指出的是，热探测材料对入射光的波长是没有分辨能力的，因此传统的热探测器的光谱响应是宽带的，而要实现窄带热探测，一般要依赖外加的分立式窄带滤光片。超构材料吸收体的引入，使热探测器在像元层次上具有独立分辨电磁波长的能力，可以在不依赖分立式窄带滤光片的前提下便实现窄带探测，这使得基于热探测像元阵列的非制冷红外焦平面有了更大的设计自由度。图13(f)展示了如何构建像元阵列，并独立调控每个像元上集成的吸收体的吸收波长，从而实现中红外波段的多波长探测功能。图13(g)给出了两个像元的响应率与入射光波长的关系曲线，即光谱响应率。这两个像元分别集成了具有不同吸收波长的吸收体，因此，它们的光谱响应率的峰值也分别位于不同的波长处。图13(h)则给出了8个像元的峰值响应波长。可以看出，通过调节金属槽阵列的单元周期，像元的峰值响应波长可以覆盖整个中红外波段。集成超构材料吸收体的热电堆像元的制造工艺流程如图13(i)所示，该流程采用了与CMOS兼容的工艺，因此可以利用集成电路芯片的生产线进行大规模生产。

 

 

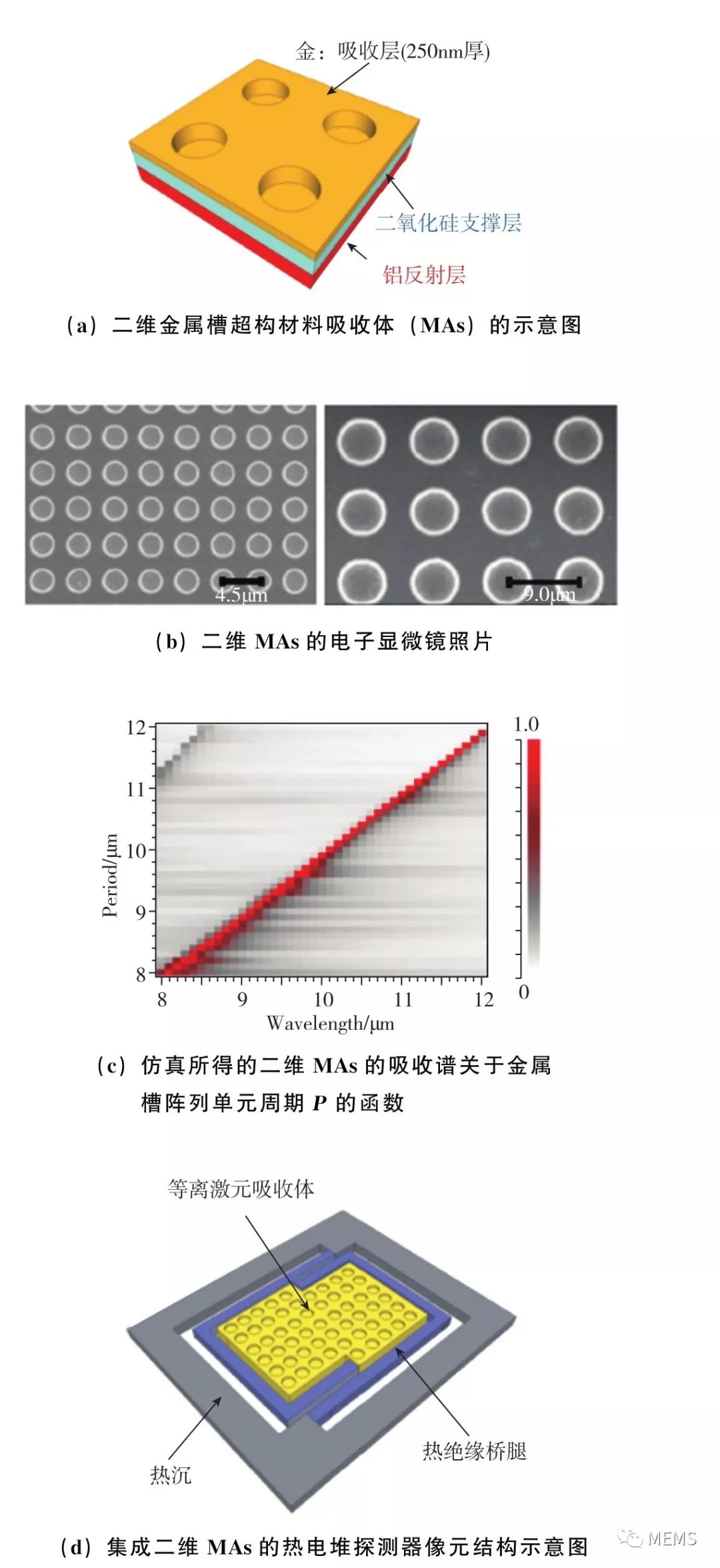
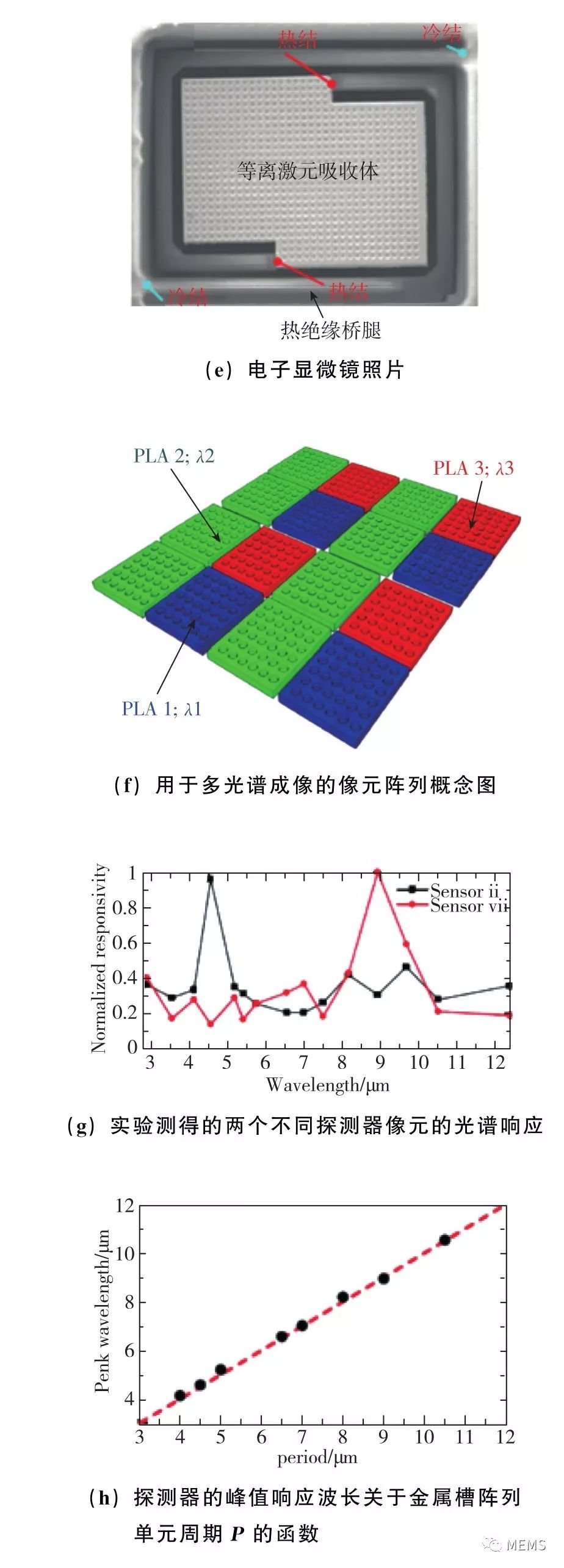
图13 利用二维周期性金属圆槽阵列调控热电堆探测器的红外光谱响应

沿着利用超构材料调控热探测器像元光谱响应的思路，Shinpei Ogawa等人进一步开发了基于SOI二极管的双色成像热探测器。如图14(a)所示，该探测器采用 “金属天线阵列-介质层-金属背板”(即MIM结构)的超构材料吸收体实现对入射光波长的选择。上层的金属天线为圆盘型，以确保对入射光的偏振态不敏感吸收。同时，在MIM结构中还留出了若干释放孔，用于形成悬空的支撑结构，如图14(b)所示。由于MIM结构的超构材料吸收体对入射光的局域化功能很强，释放孔的存在对吸收体的吸收谱影响并不大。如图14(c)所示，通过调节上层圆盘型金属天线的尺寸，便可以灵活调控吸收体的吸收波长。集成超构材料吸收体的完整像元结构及其典型光谱响应曲线如图14(d)、图14(e)所示。基于这种像元结构，作者制作了相应的焦平面阵列，如图14(f)所示。焦平面阵列的像元间距(pixel-pitch)为50μm，像元阵列的大小为320×240，整个焦平面阵列的尺寸为20.0mm×19.0mm。为实现实时的双色成像探测，像元阵列被划分为左右两半，通过调控上层金属天线的结构和大小，将左半边像元阵列的探测波长设定为4.7μm，右半边像元阵列的探测波长设定为7.6μm。为了验证双色成像探测功能，作者将一个辐射体与一个中心波长为4.7μm的窄带滤光片的组合作为探测目标。对该探测目标的成像效果如图14(g)所示。可以看到，只有左半边像元阵列可以对目标进行成像，而右半边像元阵列对探测目标没有响应，这也就验证了双色成像探测的功能。

 

图14 基于超构材料的双色红外成像探测芯片

超构材料不但可以分辨入射光的频率，还可以分辨入射光的偏振态，上述目标只需要在亚波长单元的结构中引入不对称性即可实现。例如，Shinpei Ogawa等人于2014年报道了采用椭圆形金属槽阵列作为具有偏振态选择功能的超构材料吸收体，如图15(a)、图15(b)所示。由于椭圆形金属槽具有结构不对称性，只有在入射光的电场分量平行于椭圆的短轴时才会激发谐振，因此其具有分辨偏振态的能力，如图15(c)所示。而如果将这种超构材料吸收体与热电堆探测器像元进行集成，如图15(d)、图15(e)所示，就可以调控像元响应与入射光偏振态的关系，即偏振光谱响应。从图15(f)可以看出，集成超构材料吸收体的热电堆探测器像元对两种偏振态的响应是不同的，即其具有了独立的偏振态分辨能力。对于焦平面探测器而言，这意味着可以灵活设置像元阵列中每个像元所响应的偏振态。如果将像元阵列中四个相邻的像元规定为一个超像元，并将其中每个像元所响应的偏振态按图15(g)所示的方式进行设置，就可以根据它们的读出信号，按照斯托克斯公式计算出入射光的偏振度和偏振角，这也是分焦平面式偏振成像探测的原理。

 

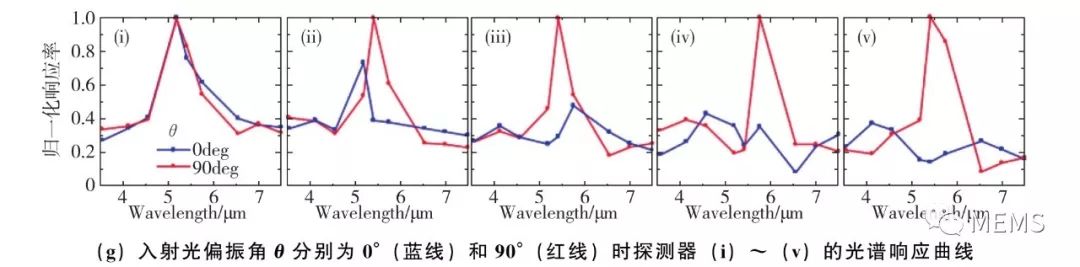
图15 利用二维椭圆金属槽阵列调控热电堆探测器的红外偏振/光谱响应

基于相同的思路，Shinpei Ogawa等人于2015年报道了采用基于条形金属槽阵列的偏振敏感型超构材料吸收体，如图16(a)、图16(b)所示。由于条型金属槽同样具有结构的不对称性，因此其也具有对入射光偏振态的分辨能力。图16(c)、图16(d)给出了集成条状金属槽阵列的热电堆探测器像元，而这种像元对两种入射光偏振态的光谱响应如图16(e)、图16(f)所示。

 

 

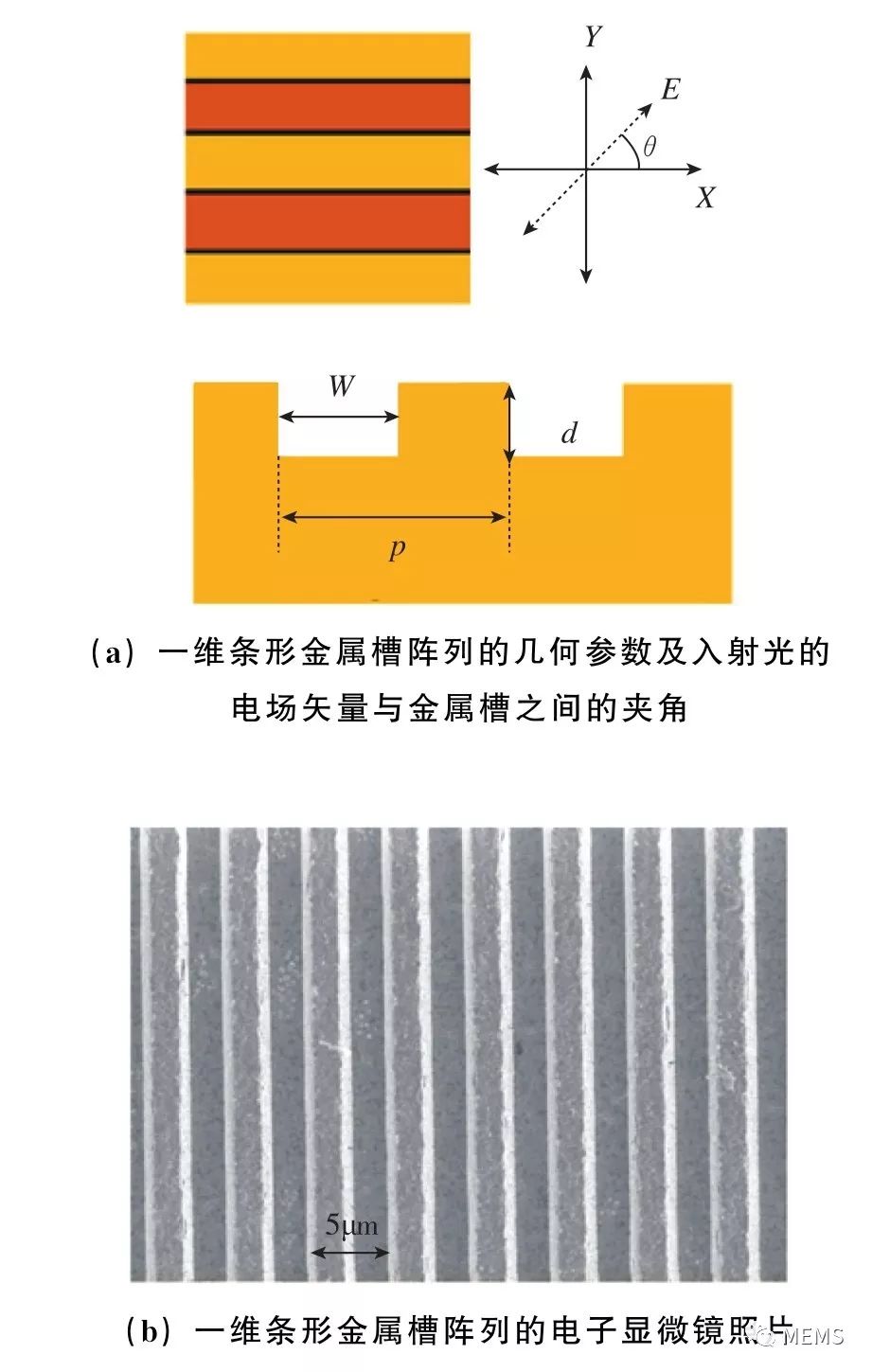
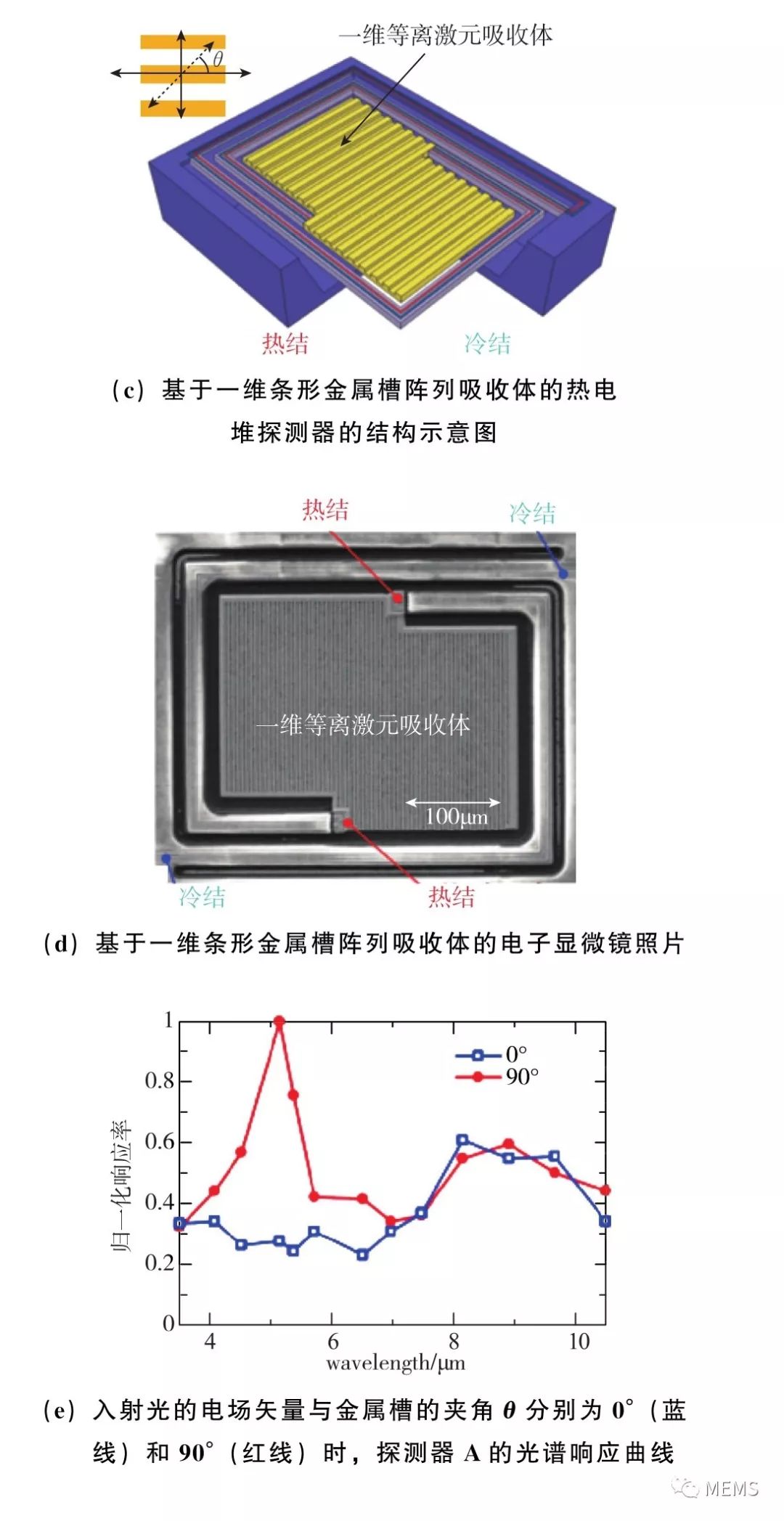
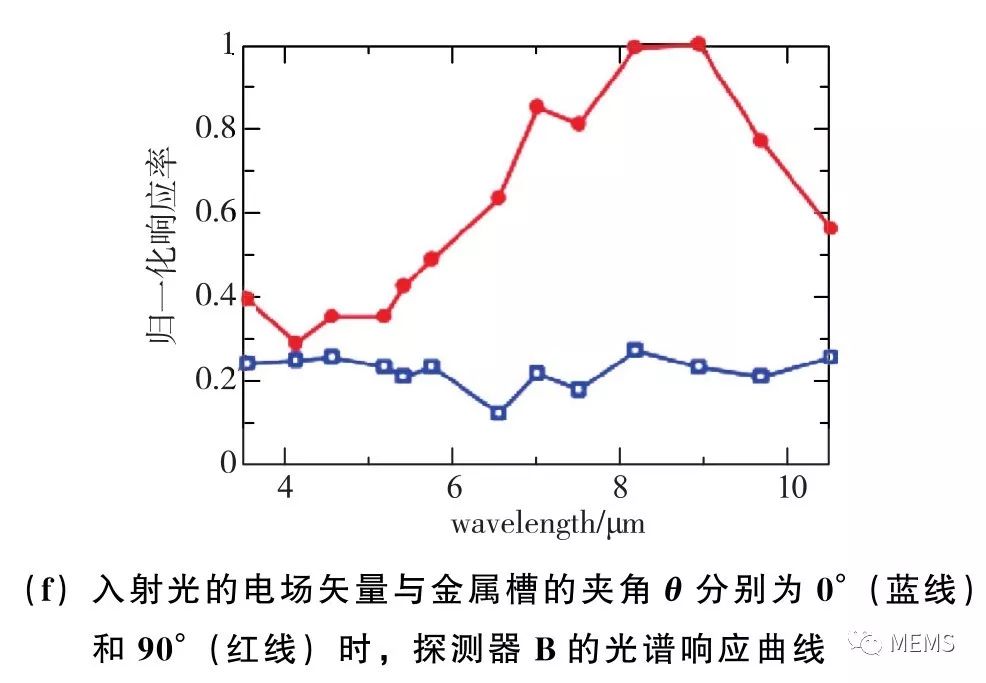
图16 利用一维周期性金属槽阵列调控热电堆探测器的红外偏振/光谱响应

本文作者与同事从2012年开始发表了一系列论文，报道了将超构材料吸收体集成在基于双材料悬臂梁的热形变探测器像元上，实现波长选择型探测和偏振选择型探测的工作。如图17(a)、图17(b)所示，热形变探测器的像元由“25nm金薄膜+100nm氮化硅薄膜”的双材料悬臂梁结构组成，臂长为500μm，宽为100μm，且两端固定。在入射红外光的照射下，悬臂梁吸收光能并将其转化为热能，导致温度升高。在温升的作用下，金薄膜与氮化硅薄膜之间的受热膨胀程度差异将导致悬臂梁发生弯曲形变，而这种弯曲形变的程度与入射光的光强成正比。因此，通过测量双材料悬臂梁结构的形变量，就可以读出入射红外光的光强。与其他类型的热探测器一样，热形变探测器对入射光的波长和偏振态也不具备分辨能力。因此，在双材料悬臂梁上集成了基于纳米槽天线阵列的超构材料吸收体，如图17(c)所示。由于纳米槽天线在结构上具有不对称性，因此只有当入射光的偏振态垂直于纳米槽时，才能激发起电磁谐振，即对入射光的偏振态具有分辨能力。当入射光的偏振态垂直于纳米槽时，电磁谐振的峰值波长与纳米槽的长度线性相关，如图17(d)所示，即对入射光的波长具有分辨能力。为了测量悬臂梁的形变量，采用了基于光纤的法布里-帕罗干涉仪结构，如图17(e)所示。在该结构中，悬臂梁是一个反射面，光纤端面是另一个反射面，两个反射面之间的间距(即干涉仪的腔长)，受到悬臂梁弯曲形变的调控。通过光纤向干涉仪注入1550nm的测试光，并根据干涉仪反射回的光的强度，便可以推算出干涉仪的腔长变化量，即悬臂梁的弯曲形变量。我们用输出光波长为6μm的中红外量子级联激光器作为光源，对该热形变探测器进行了测试，集成在悬臂梁上的纳米槽天线的峰值吸收波长也设定为6μm。图17(f)给出了纳米槽天线的吸收系数和探测器的电压响应率与入射光波长的关系。图17(g)给出了入射光在受到斩波器的调制时，探测器的响应率随调制频率的变化曲线。

 

 

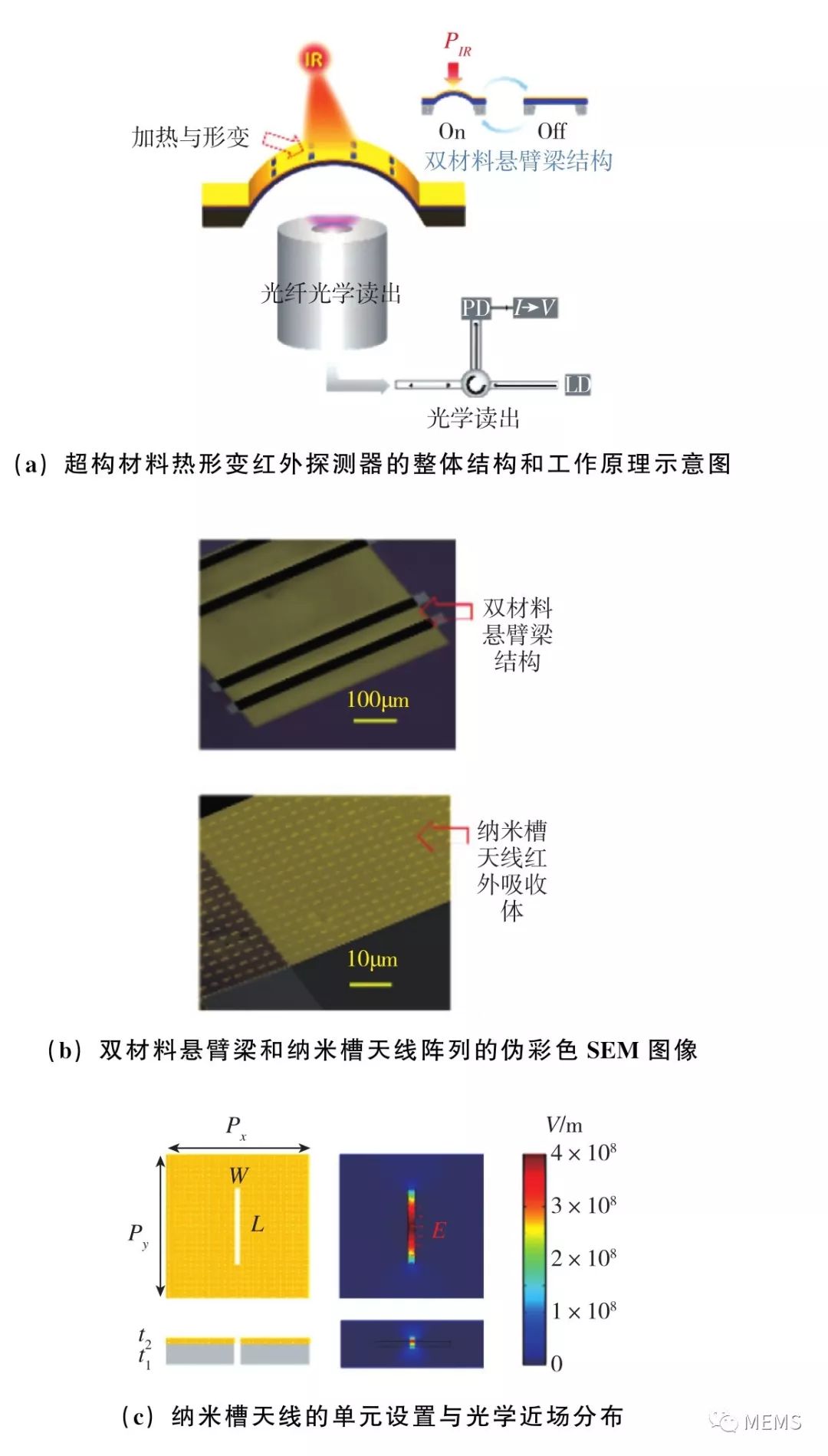
图17 利用基于纳米槽天线的超构材料吸收体调控热形变探测器的红外偏振/光谱响应

美国杜克大学的Willie Padilla等人于2017年报道了将超构材料吸收体与基于铌酸锂薄膜的热释电探测器像元进行集成、实现波长选择型探测的工作。如图18(a)所示，该探测器采用厚度为575nm的单晶铌酸锂薄膜作为热释电材料，同时热释电薄膜也构成了 “金属天线-介质层-金属背板”三层结构中的介质层。热释电薄膜的上方是分裂十字金天线阵列，如图18(b)所示，薄膜下方是金背板。天线阵列的大小为150μm×150μm，如图18(c)所示，这同时也定义了热探测器像元的大小。图18(d)给出了三层结构对入射光的典型吸收谱线。可以看出，三层结构可以选择性地吸收特定波长范围内的入射光。而通过调整上层天线阵列的结构与尺寸参数，可以灵活调控对入射光的峰值吸收波长，如图18(e)所示。当入射光波长等于峰值吸收波长时，三层结构内部的光功率损耗密度分布、温度分布及相应的热释电电场场强的分布情况由图18(f)给出。可以看出，在峰值波长处，入射光被局限在三层结构内。由于金属材料和薄膜铌酸锂材料对光均有吸收作用，吸收的光能通过欧姆损耗转化为热能并导致温度上升，而温度的上升又导致热释电薄膜上下两极之间产生电荷堆积和相应的电信号输出。图18(g)对比了该探测器的光谱响应曲线与超构材料吸收体的光谱吸收曲线。可以看出，在集成了窄带超构材料吸收体之后，探测器的光谱响应也变为了窄带的，即实现了波长选择型的探测。

 

 

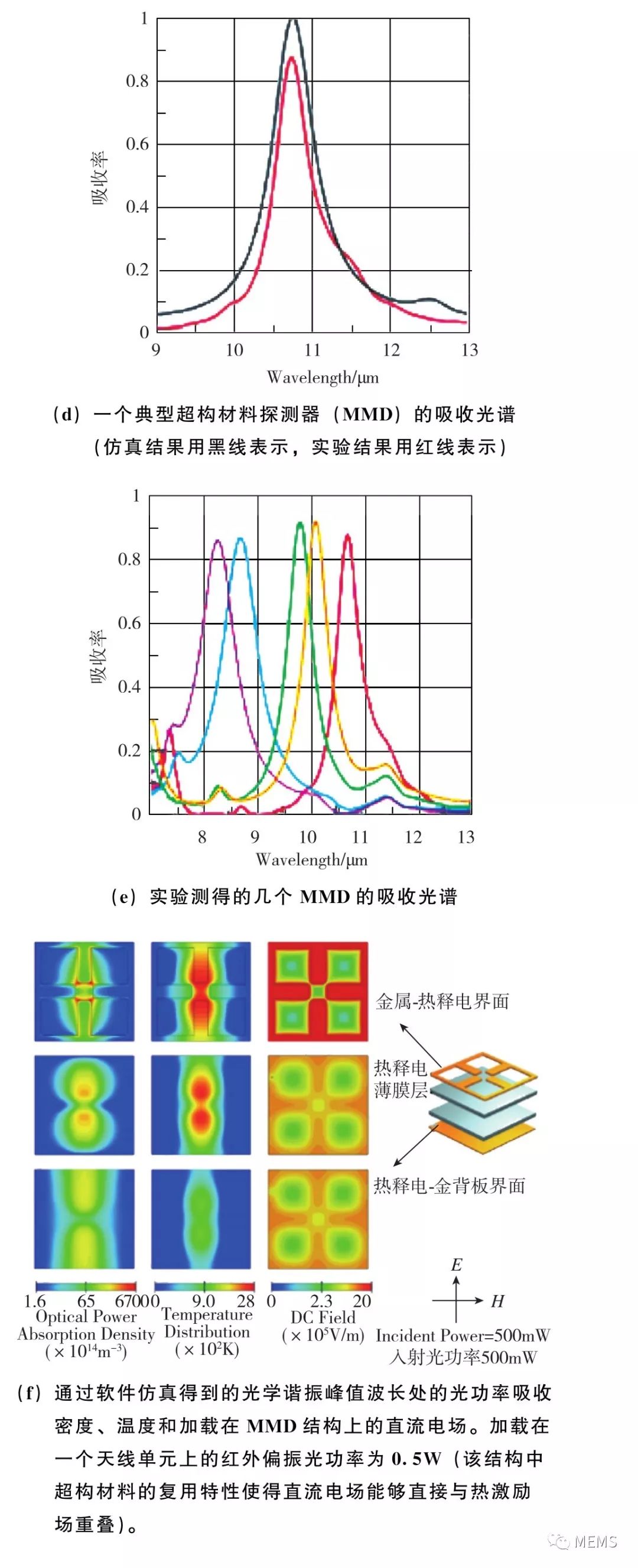
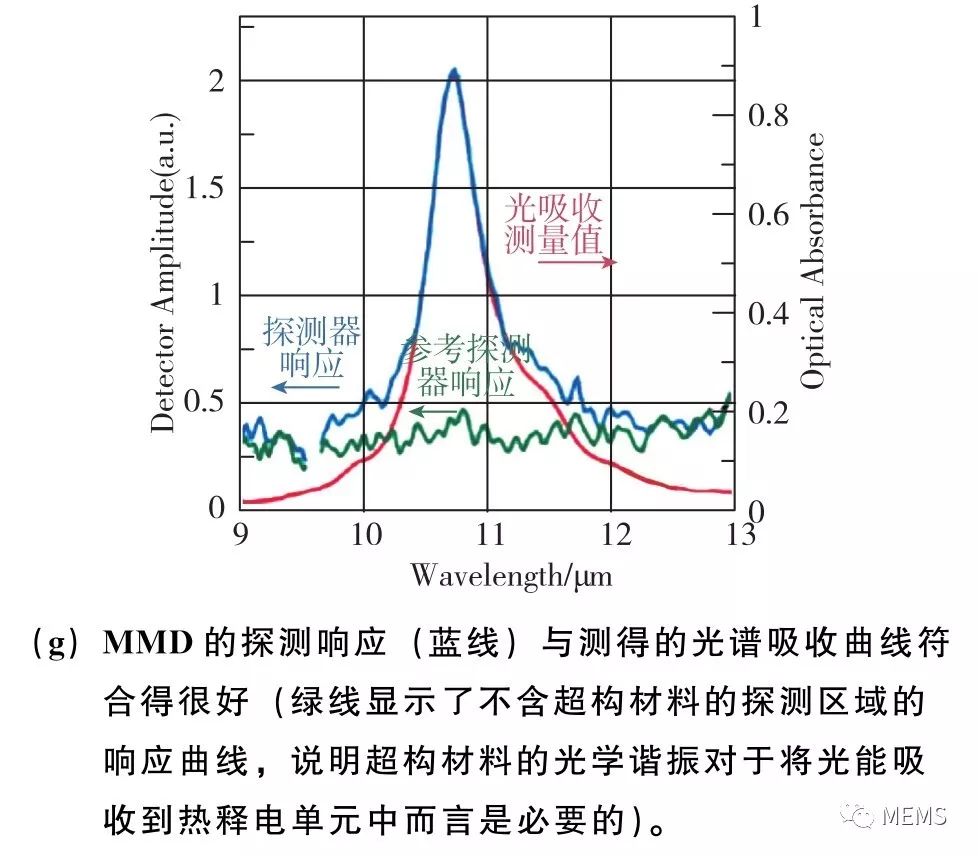
图18 利用基于分裂十字天线的超构材料吸收体调控热释电探测器的红外光谱响应

3.2 超构材料作为探测芯片的波前调控元件

在Capasso等人提出广义折反射定律并展示出基于天线阵列的平面聚焦透镜后，学术界对利用超构材料(表面)实现多功能的平面光学元件产生了浓厚的兴趣，而成像透镜作为各种光学系统的关键部件，也成为了超构材料的一个标志性的应用。从2016年开始，学术界报道了一系列基于超构材料的平面成像透镜(超透镜，metalens)的工作，这里选取两个工作在中红外波段的典型成像超透镜案例加以说明。

澳大利亚国立大学的Barry Luther-davies等人于2017年报道了基于纳米硅柱阵列的平面成像透镜。如图19(a)所示，该透镜的阵列基本单元为纳米硅柱，衬底为MgF2。纳米硅柱阵列在工作波长λ=4μm附近的振幅响应(Transmission)和相位响应(Phase)随硅柱的底面半径(Radius)及阵列单元的尺寸(Lattice Constant)的变化规律，由图19(b)、图19(c)给出。作者利用该纳米硅柱阵列进行了基本的光线偏折的验证性工作，仿真验证结果如图19(d)、图19(e)所示。为检验纳米硅柱阵列对光束聚焦的能力，作者根据式(3)所描述的相位分布函数对纳米硅柱阵列的排布进行了设计(图19(f))，并实验制备了6个直径D为300μm的纳米硅柱阵列。每个阵列的焦距f依次为50μm、100μm、150μm、200μm、250μm、300μm，对应的数值孔径依次为0.95、0.83、0.71、0.6、0.51、0.45。

 

 

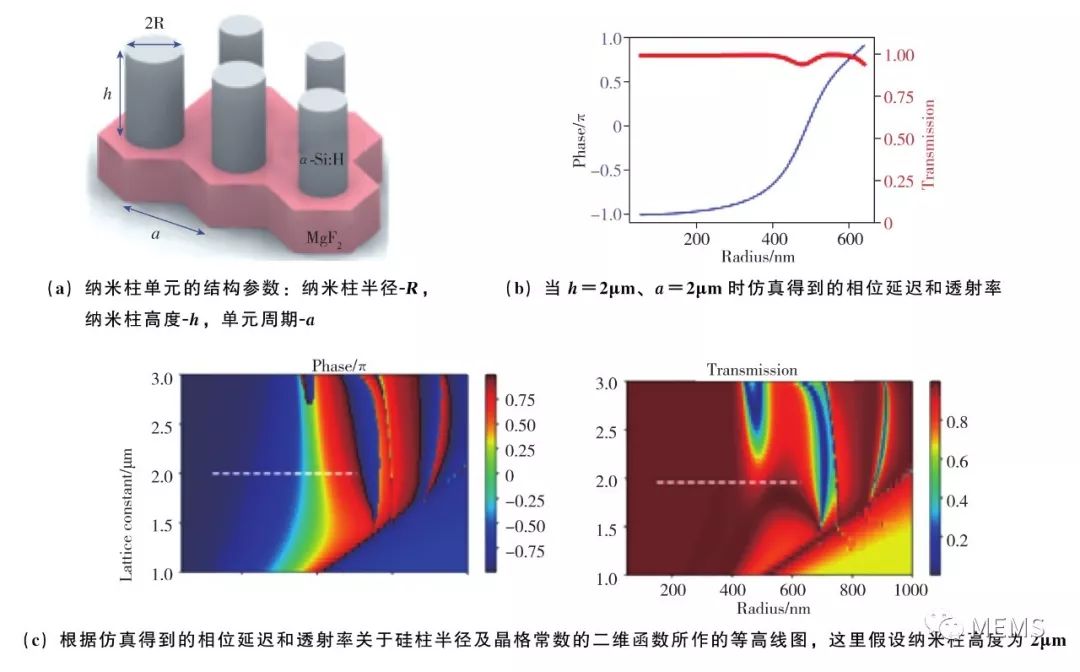
图19 基于硅纳米柱阵列的中红外超透镜

图19(i)给出了光束聚焦实验的测量结果。可以看出，该纳米硅柱阵列的聚焦能力已接近衍射极限。为检验纳米硅柱阵列的成像效果，作者制备了直径为2mm、焦距f也为2mm的纳米硅柱阵列。作者首先用该纳米硅柱阵列对自制的样品进行了成像实验，效果如图19(j)所示。随后，作者又用1951年美国空军制定的标准测试图案(图19(l))作为成像对象检验了该纳米硅柱阵列的成像效果，如图19(k)所示。结果显示，当该纳米硅柱阵列的放大倍数为120倍时，可以分辨的最小线宽为4.38μm。作为对比，作者又采用传统的非球面硫系玻璃透镜（C036TME-E, Thorlabs, NA=0.56）进行了成像实验，结果如图19(m)所示，该硫系玻璃透镜可以分辨的最小尺度为3.48μm。由于硫系玻璃透镜的数值孔径比纳米硅柱阵列的数值孔径大出约10%，作者得出的结论是，纳米硅柱阵列的分辨能力与硫系玻璃透镜的成像分辨能力相当。

美国麻省理工学院的Juejun Hu等人于2018年报道了基于碲化铅(PbTe)纳米结构阵列的平面成像透镜,衬底为氟化钙CaF2，工作波长λ0=5.2μm。为同时得到0~2π的相位响应范围和较高的透射率，纳米结构阵列中的基本单元(meta-atom)选取了长方形和H型两种结构，基本单元的周期P为2.5μm、厚度为650nm。图20(a)~图20(c)给出了长方形基本单元的结构示意图、振幅响应和相位响应。从图20(d)可以看出，虽然长方形基本单元的相位响应能够覆盖0~2π，但是在其中120°的相位响应范围内，基本单元的透射率较低 (low efficiency gap)。因此，作者引入了H型的基本单元结构，如图20(e)所示。从图20(f)可以看出，H型结构能够有效填补长方形结构透射率较低的相位响应范围。将两种结构结合起来,就可得出相位响应范围覆盖0~2π、同时透射率又较高的一组基本单元,如图20(g)所示。作者基于设计好的基本单元进行了平面透镜的制备。图20(h)、图20(i)给出了碲化铅薄膜的折射率和消光系数的实际测量值，以及实验制备的长方形和H型基本单元的扫描电镜图。图20(j)~图20(l)给出了用作平面成像透镜的纳米结构阵列的扫描电镜图。该平面透镜的直径为1mm，焦距f=0.5mm。作者用1951年美国空军制定的测试图案对平面透镜进行了成像实验,如图20(m)所示。实验测得的成像分辨率为3.9μm，与在衍射极限条件下采用瑞利判据的理论计算值3.4μm接近。

事实上，采用H型等一些不同于圆柱、长方体的结构，以此来填补在相位响应覆盖上的不足这种方法，在目前的超透镜研究领域具有非常普遍的应用。在对单元的设计中，半径这一自由度可以用来调控相位响应，以此实现聚焦成像功能。而当要给予超透镜其他附加的功能(比如消除色差时)，就需要另外的一个自由度。将纳米阵列的形状由圆柱、长方体改为其他形状，正是引入新的自由度的方法。

 

 

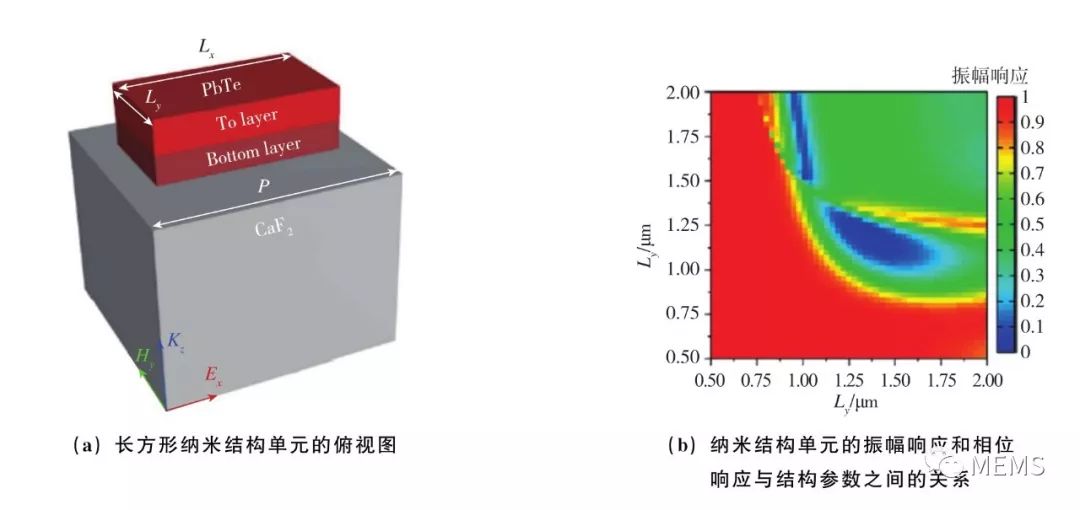
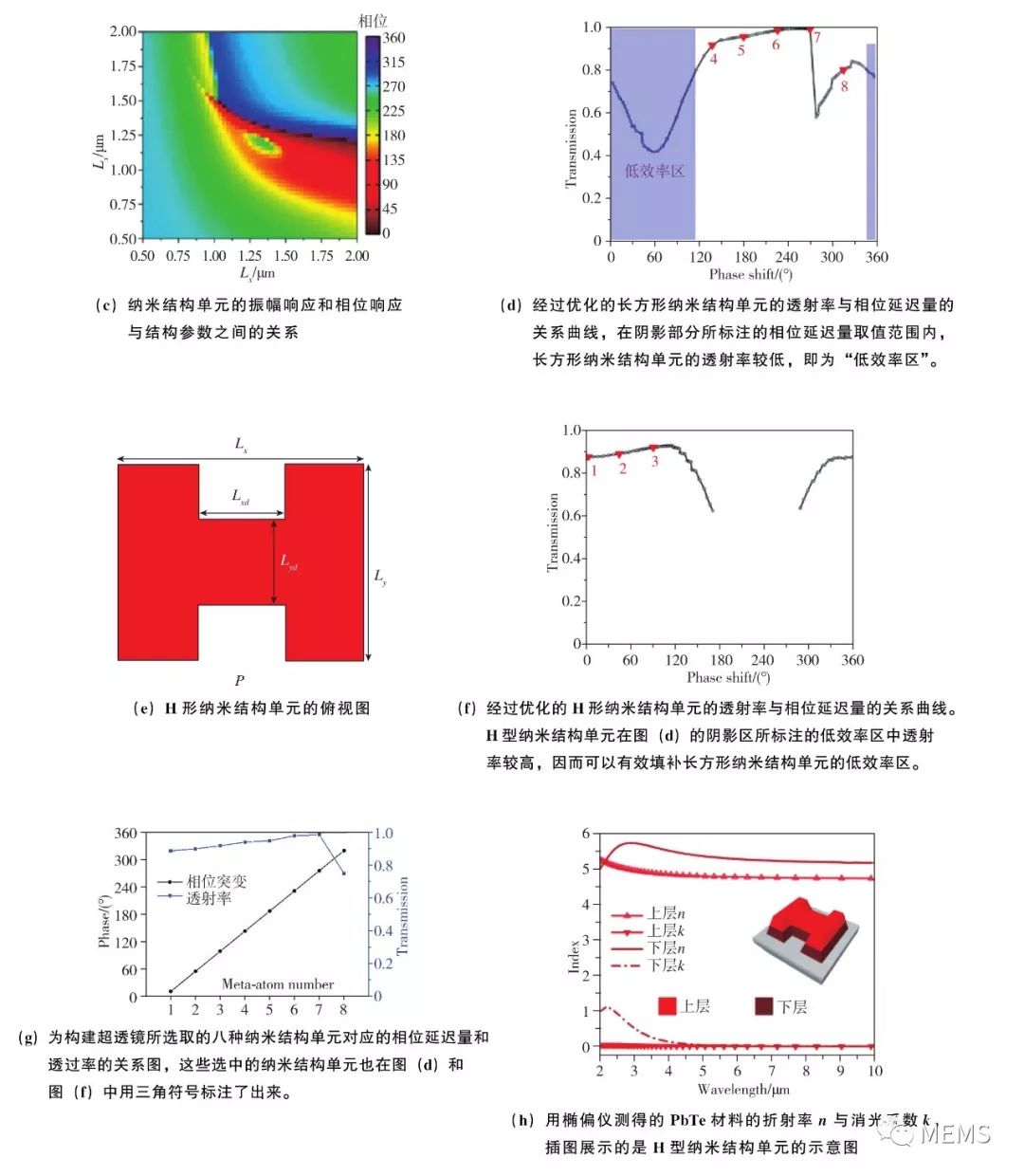
图20 基于PbTe纳米结构单元阵列的中红外超透镜