如何实现乘法器电路的设计?方案有哪些?
一个理想的通用乘法器,不应当对任何一个输入信号的极性加以限制,也就是说,应当具有能完成四个象限的运算功能的电路。
乘法器电路的设计是数字电路的核心问题之一,主要有以下几种实现方案,各有优劣,适用于不同的场景(速度、面积、功耗):
一、 基本原理与基础方案
-
移位-加乘法器:
- 原理: 模仿手算乘法。将一个操作数(被乘数)与另一个操作数(乘数)的每一位(从最低位到最高位)相乘(实际上是
与操作),产生部分积。然后根据乘数当前位的权重(2^k),将部分积左移 k 位,最后将所有移位后的部分积相加,得到最终乘积。 - 实现方式 (串行):
- 设计一个状态机或计数器。
- 在每个时钟周期:
- 检查乘数的最低位(LSB)。
- 如果为
1,则将当前的被乘数(或累加值)加到结果寄存器中。 - 将被乘数寄存器左移一位(相当于乘以2,为下一位做准备)。
- 将乘数寄存器右移一位(将下一位移到LSB位置)。
- 重复直到乘数所有位都处理完(计数器归零或乘数为零)。
- 特点:
- 优点: 结构简单,占用芯片面积小(面积优),控制逻辑简单。
- 缺点: 速度慢,完成一次乘法需要 N 个时钟周期(N 为乘数的位数)。
- 适用场景: 对速度要求不高、资源受限(如低功耗微控制器)的应用。
- 原理: 模仿手算乘法。将一个操作数(被乘数)与另一个操作数(乘数)的每一位(从最低位到最高位)相乘(实际上是
-
阵列乘法器:
- 原理: 完全展开移位-加的过程,将所有部分积的生成和加法用硬连线并行实现。常见形式是类似于手算乘法竖式排列的二维单元阵列。
- 实现方式 (并行):
- 部分积生成: 使用二维阵列的
AND门,被乘数的每一位分别与乘数的每一位相与,产生 N*N 个部分积位P[i][j](i 是被乘数位下标, j 是乘数位下标)。 - 部分积累加:
- 每一列的所有部分积位(P[0][j], P[1][j], ..., P[N-1][j])需要相加,并产生该列的最终和位以及向上一位的进位。
- 加法器通常采用行波进位加法器或效率更高的加法器结构(如先行进位)。
- 正确对齐部分积:权重为 j 的乘数位产生的部分积位 P[i][j] 的有效位置是 i+j。
- 部分积生成: 使用二维阵列的
- 特点:
- 优点: 纯组合逻辑,速度较快(关键路径长度约为 O(N)),一个时钟周期(或纯组合逻辑延迟)即可得到结果。
- 缺点: 占用面积非常大 (O(N^2)),随着位数增加功耗和布线复杂度急剧上升。
- 适用场景: 对速度有较高要求,且能接受较大面积的应用。
二、 优化方案 (提升速度或减少面积)
-
Booth 编码乘法器:
- 原理: 对乘数进行重新编码(Booth 编码或 Modified Booth 编码),减少部分积的数量(通常减少到接近 N/2)。通过检查乘数的位对(如 2 位或 3 位)来决定操作:+0、+1*被乘数、+2*被乘数、-1*被乘数、-2*被乘数等。实现负数操作通常使用被乘数的补码形式。
- 实现方式:
- 编码器:根据乘数位段生成部分积选择信号(sel)和符号信号(控制是否取反)。
- 部分积生成:根据选择信号
sel,选择 0、被乘数、2*被乘数(左移一位)等。 - 符号处理:若需要负数部分积,则生成其补码(通常是取反后在最低位注入
1的进位)。 - 压缩网络/加法树:将产生的更少的(但可能稍宽)部分积累加。
- 特点:
- 优点: 显著减少部分积数量(约减半),加快了累加速度(需要加的次数更少),节省了面积,特别高效地处理有符号数。
- 缺点: 控制逻辑比基本移位加复杂,编码和符号处理增加了部分开销。
- 适用场景: 最主流的通用乘法器实现技术,广泛应用于 CPU、DSP、高性能 ASIC/FPGA 设计。
-
华莱士树 / Dadda 树乘法器:
- 原理: 使用更高效的加法器结构(压缩器)对部分积进行累加。它们不直接使用全加器串联,而是用计数器 (Counter) 和压缩器 (Compressor) (如 3:2 压缩器即全加器、4:2 压缩器、5:3 压缩器等) 构成树状结构,并行压缩多个部分积。目标是最小化加法树的高度。
- 实现方式:
- 部分积生成: (通常配合 Booth 编码) 产生多个部分积。
- 压缩树:
- 华莱士树: 在每个层级,尽可能多地将三个部分积压缩为一个和与一个进位(使用全加器/3:2 压缩器)。直到只剩下两行(加数和进位)。
- 达达树: 预先定义一个最优的压缩目标高度,按特定规则在每一级尽可能减少行数达到该目标。结构更规则,布线可能更优。
- 最终相加: 将压缩树输出的两行(通常是向量 S 和向量 C)通过一个快速加法器(如超前进位加法器)相加得到最终结果。
- 特点:
- 优点: 速度非常快(加法树高度约为 O(log₃(N))),是目前实现高速乘法器的主流方案。
- 缺点: 结构复杂,布线的扇入扇出问题更突出,面积和功耗可能较大(虽然压缩次数少但单元复杂),设计复杂度高。
- 适用场景: 对速度要求极高的应用,如高性能 CPU、GPU、浮点运算单元的核心部分。常与 Booth 编码结合使用。
-
查找表乘法器:
- 原理: 预先计算好所有可能的输入组合(小位宽时可行)对应的乘积,存储在 ROM 或组合逻辑实现的查找表中。输入操作数作为地址线,直接输出结果。
- 实现方式: 小位宽时直接使用组合逻辑(硬连线)或 ROM 实现查找表。
- 特点:
- 优点: 对于非常小的位宽(如 4x4 bit, 有时做到 8x8 bit),速度最快(查找表延迟),设计简单。
- 缺点: 面积随位宽指数级增长 (O(2^(2N))),位宽稍大就完全不实用。
- 适用场景: 极低位数的乘法或作为其他乘法器中处理小规模部分的组件。
三、 方案选择与权衡
选择哪种乘法器设计方案取决于具体应用的需求:
- 速度优先 (高性能计算): Booth 编码 + 华莱士树 / Dadda 树 + 超前进位最终加法器 是黄金组合。
- 面积/功耗优先 (低功耗嵌入式): 串行移位-加乘法器 或 较小的并行阵列乘法器。
- 平衡速度与面积 (通用场景): Booth 编码 + 简化阵列结构 或较小的树结构是常用选择。
- 小位宽专用: 查找表乘法器 可能最优。
- 有符号数: Booth 编码 天生适合处理有符号数(补码),其他方法通常需要额外处理符号。
- FPGA 实现: FPGA 有专用 DSP Slice,通常包含高度优化的预加法器、乘法器(可能是基于 Booth 和压缩树)、累加器,应优先利用这些硬核资源。
- ASIC 实现: 设计自由度更高,需要综合权衡时序、面积、功耗,Booth+树结构是高性能首选。
总结:
乘法器设计是一个在速度、面积、功耗、设计复杂度之间做精细平衡的过程。从最慢但面积最小的串行移位-加,到折中的基本阵列/带 Booth 的阵列,再到追求极限速度的Booth+华莱士/达达树,以及只在极小位数可用的查找表,工程师根据具体需求选择最适合的方案。现代高性能处理器普遍采用 Booth 编码结合各种高度优化的压缩树结构来实现快速的乘法运算。
采用Gillbert单元如何实现CMOS模拟乘法器的应用设计
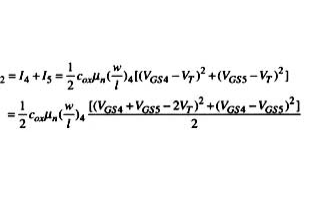
在集成电路系统中,模拟乘法器在信号调制解调、鉴相、频率转换、自动增益控制和功率因数校正控制等许多方面有着非常广泛的应用。实现模拟
2021-03-23 09:40:19
基于FPGA的16位乘法器的实现
本设计以16位乘法器的设计为基础,从而掌握现代大规模集成数字逻辑电路的应用设计方法,进一步掌握电子仪器的正确使用方法,以及掌握利用计算机进行电子设计自动化(EDA)的基本方法。由16位加
资料下载
![]() 姚小熊27
2021-06-01 09:43:56
姚小熊27
2021-06-01 09:43:56
集成电路中低功耗乘法器的实现与设计
限度的低功耗效果。本文紧跟市场发展动向,从以上应用角度出发,着力研究集成电路设计中小数乘法器的前端低功耗算法以及实现技术,并且改进了现有低功耗设
资料下载
佚名
2021-04-08 17:01:02
乘法器原理_乘法器的作用

乘法器(multiplier)是一种完成两个互不相关的模拟信号相乘作用的电子器件。它可以将两个二进制数相乘,它是由更基本的加法器组成的。乘法器可
2021-02-18 15:08:01
如何实现一个四输入乘法器的设计
乘法器(multiplier)是一种完成两个互不相关的模拟信号相乘作用的电子器件。它可以将两个二进制数相乘,它是由更基本的加法器组成的。乘法器可
2019-11-28 07:06:00
怎么设计基于FPGA的WALLACETREE乘法器?
在数字信号处理中,乘法器是整个硬件电路时序的关键路径。速度和面积的优化是乘法器设计过程的两个主要考虑因素。由于现代可编程逻辑芯片FPGA的集成度
基于CMOS工艺下的Gillbert单元乘法器的研究
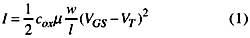
在集成电路系统中,模拟乘法器在信号调制解调、鉴相、频率转换、自动增益控制和功率因数校正控制等许多方面有着非常广泛的应用。实现模拟
2019-05-31 08:20:00
采用CSA与4-2压缩器改进Wallace树型乘法器的设计
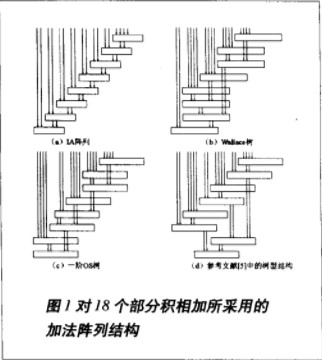
在微处理器芯片中,乘法器是进行数字信号处理的核心,同时也是微处理器中进行数据处理的关键部件。乘法器完成一次操作的周期基本上决定了微处理器的主频。乘法器
2019-05-15 08:27:00
 换一换
换一换
- 如何分清usb-c和type-c的区别
- 中国芯片现状怎样?芯片发展分析
- vga接口接线图及vga接口定义
- 华为harmonyos是什么意思,看懂鸿蒙OS系统!
- 芯片的工作原理是什么?
- ssd是什么意思
- 什么是蓝牙?它的主要作用是什么?
- 汽车电子包含哪些领域?
- TWS蓝牙耳机是什么意思?你真的了解吗
- 什么是单片机?有什么用?
- 升压电路图汇总解析
- plc的工作原理是什么?
- 再次免费公开一肖一吗
- 充电桩一般是如何收费的?有哪些收费标准?
- ADC是什么?高精度ADC是什么意思?
- EDA是什么?有什么作用?
- 中科院研发成功2nm光刻机
- 苹果手机哪几个支持无线充电的?
- dtmb信号覆盖城市查询
- 怎样挑选路由器?
- 华为芯片为什么受制于美国?
- 元宇宙概念股龙头一览
- type-c四根线接法图解
- 锂电池和铅酸电池哪个好?
- 什么是场效应管?它的作用是什么?
- 如何进行编码器的正确接线?接线方法介绍
- 虚短与虚断的概念介绍及区别
- 晶振的作用是什么?
- 大疆无人机的价格贵吗?大约在什么价位?
- 苹果nfc功能怎么复制门禁卡
- 单片机和嵌入式的区别是什么
- amoled屏幕和oled区别
- 复位电路的原理及作用
- BLDC电机技术分析
- dsp是什么意思?有什么作用?
- 苹果无线充电器怎么使用?
- iphone13promax电池容量是多少毫安
- 芯片的组成材料有什么
- 特斯拉充电桩充电是如何收费的?收费标准是什么?
- 直流电机驱动电路及原理图
- 自举电路图
- 通讯隔离作用
- 苹果笔记本macbookpro18款与19款区别
- 新斯的指纹芯片供哪些客户
- 传感器常见类型有哪些?
- 伺服电机是如何进行工作的?它的原理是什么?
- 无人机价钱多少?为什么说无人机烧钱?
- 以太网VPN技术概述
- 手机nfc功能打开好还是关闭好
- 十大公认音质好的无线蓝牙耳机