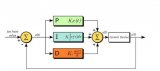
pid调节参数整定的方法有哪些？有哪些小妙招？

PID参数的调试是一个综合的、各参数互相影响的过程，实际调试过程中的多次尝试是非常重要的，也是必须的。

好的，PID参数（比例P、积分I、微分D）整定是控制系统设计和调试的核心环节，目的就是让系统响应又快、又稳、又准。以下是常用的整定方法以及一些实用的小妙招：

常用PID参数整定方法

试凑法：
- 描述： 最基础、最直观的方法。基于对系统特性和PID参数作用的理解，通过观察系统响应（如阶跃响应曲线），逐步调整参数值。
- 步骤：
  1. D=0, I=∞（或积分时间Ti=∞，禁用积分），仅调比例增益P：从小到大增加P，直到系统出现持续的等幅振荡（临界状态）。此时的P值记为K_c（临界增益）。
  2. 将P设置为一个稍小的安全值（如0.5*K_c）。
  3. 引入积分I（减小积分时间Ti）：逐渐减小Ti（增大积分作用），消除静差。观察系统是否变慢或超调变大，找到一个平衡点。
  4. 引入微分D（增加微分时间Td）：如果系统有超调或调节时间长，逐渐增大Td（增强微分作用），观察抑制超调和加快稳定的效果。
- 优点： 简单直接，无需数学建模，适用于各种系统。
- 缺点： 费时费力，依赖调试者的经验和感觉，可能找不到最优参数。
临界比例度法（Ziegler-Nichols方法）
- 描述： Z-N法中最常用的一种，基于临界增益K_c和临界振荡周期P_c。是一种启发式公式法。
- 步骤：
  1. 仅用比例控制（I=∞, D=0），从小到大调节P，直到系统产生稳定而持续的等幅振荡（临界振荡）。
  2. 记录此时的比例增益K_c（临界增益）和振荡周期P_c（临界周期）。
  3. 根据公式计算PID参数：
    - P: P = 0.6 * K_c
    - I (积分时间Ti): Ti = 0.5 * P_c
    - D (微分时间Td): Td = 0.125 * P_c
- 优点： 相对试凑法更系统化，能快速获得一组可用的参数（尤其对于快速响应系统）。
- 缺点： 需要系统能够产生等幅振荡（对某些系统不安全或不适用）。公式给出的参数通常偏“积极”，鲁棒性可能不够好（需进一步微调）。
衰减曲线法：
- 描述： Z-N法的改良版，避免临界振荡，追求4：1衰减比（超调量约25%）的响应曲线。
- 步骤：
  1. 仅用比例控制（I=∞, D=0）。
  2. 调整P，使阶跃响应的衰减比达到4：1（即振荡一个波峰后，第二个波峰衰减到第一个波峰幅值的1/4）。
  3. 记录此时的比例增益K_s（衰减比例增益）和振荡周期P_s（衰减振荡周期）。
  4. 根据公式计算PID参数（常见公式）：
    - P: P = K_s
    - I (积分时间Ti): Ti ≈ P_s / 1.5 （不同公式略有差异，如P_s/1.2， P_s/2.0等）
    - D (微分时间Td): Td ≈ P_s / 6 （不同公式略有差异，如P_s/8等）
- 优点： 比临界比例度法更安全，不需临界振荡，鲁棒性通常更好。
- 缺点： 需要系统能产生振荡才能识别P_s。
反应曲线法（阶跃响应法）：
- 描述： Z-N法的另一种形式，基于被控对象开环阶跃响应的特征参数。
- 步骤：
  1. 让系统在开环状态下，手动施加一个小的阶跃输入。
  2. 记录过程变量的响应曲线。
  3. 在响应曲线的最大斜率处做切线，确定：
    - 滞后时间τ： 输入变化到响应曲线开始明显变化的延迟时间。
    - 时间常数T： 切线达到稳定值的63.2%所需的时间。
    - 增益K： 输入变化量与稳态输出变化量之比（过程放大倍数）。
  4. 根据公式（如Cohen-Coon法、齐格勒-尼科尔斯法公式变种）计算PID参数。例如经典的Cohen-Coon法（追求1/4衰减）：
    - P控制器增益： Kc = (1.35 / K) * (T/τ) + (0.27 / K) （更多用于PI/PID）
    - Ti： Ti = [2.5 τ + (0.5 τ² / T)] / [1 + 1.2 * (τ/T)]
    - Td： Td = [0.37 τ T] / [T + 0.2 * τ]
- 优点： 适用于无法闭环振荡的系统，无需进行闭环测试。
- 缺点： 需要对响应曲线做切线（有主观性），模型精度有限，尤其是对非线性系统。需要系统能被开环测试。
内模控制法：
- 描述： 基于内模原理（Internal Model Principle）的整定方法，需要被控对象的数学模型（传递函数）。
- 步骤：
  1. 获取或辨识对象的数学模型G_p(s)。
  2. 设计一个鲁棒滤波器F(s)（通常是一阶或二阶低通滤波器，其时间常数λ是主要可调参数），处理模型误差和噪声。
  3. 通过IMC结构转换成等效的PID控制器形式。
  4. 通过调整滤波器的时间常数λ来权衡响应速度、鲁棒性和抗干扰性。λ越大，系统响应越慢但越鲁棒、抗噪声；λ越小，响应越快但鲁棒性越差、对噪声越敏感。
- 优点： 理论基础好，鲁棒性设计直观，参数λ有明确的物理意义（控制速度与鲁棒性的权衡）。
- 缺点： 需要相对准确的数学模型。

PID参数整定的实用小妙招

“分批调试”原则：
- 先调P增益：目标是让系统反应速度快起来（减小上升时间），但要避免超调过大或振荡。
- 再调I作用（积分时间Ti）：目标是消除静差（稳态误差），但小心超调增加和调节时间延长，Ti太大效果弱，Ti太小易振荡。
- 最后调D作用（微分时间Td）：目标是抑制超调、增加阻尼、缩短调节时间、抵抗扰动。Td过小效果差，Td过大会放大噪声或引起振荡。注意： 此原则并非绝对，有时需要交叉调整，但对新手很友好。
“由慢到快”原则： 尤其对于初次调试、或难以快速获得稳定响应的系统，开始时将参数设置得保守一些（P较小、Ti较大、Td=0），响应可能缓慢但稳定，然后逐步“加速”（增加P、减小Ti）并适当引入D，避免系统一上来就进入不稳定状态导致损坏或失控。
防止积分饱和：
- 这是非常非常重要的技巧！当执行器达到极限（如阀门全开或全关）且误差持续存在时，积分项会累积到非常大（“饱和”）。一旦误差反向，积分项需要很长时间才能从饱和值“退饱和”，导致系统响应延迟和大幅超调。
- 妙招： 实施抗积分饱和措施：
  - 积分限幅： 限制积分项的最大/最小值。
  - 积分分离/死区： 在误差很大或者输出饱和时，暂停积分作用（仅使用PD控制）。
  - 后向计算/复位终止： 当控制器输出饱和时，将反馈值设定为控制器输出刚好不饱和时的值，使积分作用不继续累积。
- 温度系统在启动阶段、流量或压力系统在设定值大幅变化时极易遇到此问题。
利用“干扰观测”法： 如果安全可行，在系统稳定后，手动给系统施加一个小的干扰（如轻敲被控对象或用注射器加液）。观察控制器如何克服这个干扰：
- 响应太慢或无法恢复？可能需要增大P或减小Ti（增强控制）。
- 恢复过程振荡？增大Ti或减小P/Td（减小控制力度）。
- 恢复后仍有静差？需要减小Ti（加强积分）。
关注波形细节：
- 爬升缓慢（上升时间长）： P不够大或Ti太大。
- 超调大： P太大或Ti太小或D不够（也可能需要增大Ti或D）。
- 调节慢（恢复时间/稳定时间长）： Ti太大或P太小（也可能需要增加D）。
- 静差（稳态误差）： Ti太大（积分作用太弱）。
- 持续振荡： 通常P太大，也可能是Ti太小或Td太大。
- 控制输出“颤抖”（高频抖动）： 很可能是D作用太强或者引入了过大的测量噪声，需要减小Td或加强信号滤波。
善用软件工具：
- 示波器/趋势图： 必须同时观察设定值、过程变量PV、控制器输出的曲线！缺一不可！控制器输出曲线能告诉你控制动作的实际情况（如积分饱和）。
- 自整定功能： 很多现代控制器（如PLC、DCS、智能仪表、LabVIEW等）都内置自动PID整定算法。选择合适的方式（如阶跃测试、继电器振荡等），让软件帮你找参数起点，再微调。非常好用！
- 仿真工具： 如有数学模型，可在MATLAB/Simulink、Python Control库等软件中进行仿真整定，更安全高效，优化目标明确。
噪声处理：
- 微分项D对高频噪声极其敏感！会放大噪声导致系统抖动甚至不稳定。
- 妙招： 在微分的输入端或输出端加入一个低通滤波器（一阶滞后环节）。滤波器时间常数需要仔细调整：太小起不到滤波作用，太大减弱了D的有用作用并增加滞后。常用方法是将滤波器的截止频率设定在所需有用信号带宽和噪声频率之间。
“变增益”法：
- 妙招： 当系统在不同工作点、不同负载下动态特性变化较大时，单一参数可能不够。采用非线性或变增益PID：
  - 非线性PID： 如P增益随误差增大而增大（非线性部分）。
  - 增益调度： 根据可测量的辅助变量（如流量、负荷），使用不同的PID参数表，在不同工况下切换参数。
鲁棒性优先： 对于需要长期稳定运行的系统，一味追求快速响应可能牺牲稳定性。特别是对于模型不确定或负载经常变化的系统（如反应器温度、供水系统），有经验的设计者会主动牺牲一点速度，换取更强的鲁棒性（即参数在一定变化范围内系统仍能稳定工作）。在衰减曲线法或内模控制法中，选择更保守的参数就是增加鲁棒性。
记录、总结与再验证：
- 认真记录每一次的调整和观察到的响应变化。
- 整定完成后，在不同工况、不同设定值下测试系统表现，验证鲁棒性。
- 为类似的系统建立参数库或经验规则。