线性代数知识点总结
线性代数知识点总结 线性代数是一种人为设计的领域特定语言(DSL),它建立了一套模型并通过符号系统完成语法和语义的映射。
以下为线性代数核心知识点总结(中文版),涵盖基本概念、核心理论及应用:
一、基础概念
- 向量 (Vector)
- 定义:具有大小和方向的量,如 (\mathbf{v} = \begin{pmatrix} v_1 \ v_2 \ \vdots \ v_n \end{pmatrix})。
- 运算:加法、数乘、点积((\mathbf{u} \cdot \mathbf{v} = \sum u_i v_i))、叉积((\mathbb{R}^3))。
- 矩阵 (Matrix)
- 定义:(m \times n) 数表,(A = [a_{ij}])。
- 特殊矩阵:
- 单位矩阵 (I)(对角元素为1)。
- 对角矩阵(非对角元素为0)。
- 对称矩阵((A = A^T))。
- 正交矩阵((A^T A = I))。
二、矩阵运算
- 基本运算
- 加法/减法:同型矩阵对应元素相加减。
- 数乘:标量乘以每个元素。
- 矩阵乘法
- 定义:(C = AB),其中 (c_{ij} = \sumk a{ik} b_{kj})。
- 性质:结合律 ((AB)C = A(BC)),分配律 (A(B+C) = AB + AC),不满足交换律((AB \neq BA))。
- 转置 (Transpose)
- 定义:(A^T) 的第 (i) 行为 (A) 的第 (i) 列。
- 性质:((AB)^T = B^T A^T),((A^T)^T = A)。
- 逆矩阵 (Inverse)
- 定义:若 (AA^{-1} = I),则 (A) 可逆。
- 性质:((AB)^{-1} = B^{-1}A^{-1}),((A^T)^{-1} = (A^{-1})^T)。
- 行列式 (Determinant)
- 定义:方阵 (A) 的标量值,记为 (\det(A)) 或 (|A|)。
- 性质:
- (\det(AB) = \det(A)\det(B))。
- (\det(A^T) = \det(A))。
- 行列式为0 ⇨ 矩阵不可逆。
三、线性方程组
- 表示形式:(A\mathbf{x} = \mathbf{b}),其中 (A) 为系数矩阵,(\mathbf{x}) 为未知向量。
- 解法:
- 高斯消元法:通过行变换化阶梯形。
- 行最简形 (RREF):判断解的存在性:
- 无解:增广矩阵出现 ([0 \cdots 0 | c])((c \neq 0))。
- 唯一解:系数矩阵满秩(秩=未知量个数)。
- 无穷解:秩 < 未知量个数。
- 解的表示:
- 特解 + 齐次解((A\mathbf{x} = \mathbf{0}) 的通解)。
四、向量空间
- 向量空间 (Vector Space)
- 定义:对加法和数乘封闭的集合(如 (\mathbb{R}^n))。
- 子空间 (Subspace)
- 条件:包含零向量,且对加法和数乘封闭。
- 基 (Basis) 和维数 (Dimension)
- 基:线性无关且生成整个空间的向量组(如 (\mathbb{R}^3) 的标准基 ({\mathbf{e}_1, \mathbf{e}_2, \mathbf{e}_3}))。
- 维数:基的向量个数((\dim(V)))。
- 秩 (Rank)
- 定义:矩阵列空间(或行空间)的维数。
- 性质:(\text{rank}(A) = \text{rank}(A^T)),且 (\text{rank}(A) \leq \min(m,n))。
五、特征值与特征向量
- 定义
- 对 (n \times n) 矩阵 (A),若 (A\mathbf{v} = \lambda \mathbf{v})((\mathbf{v} \neq \mathbf{0})),则 (\lambda) 为特征值,(\mathbf{v}) 为特征向量。
- 求解方法
- 解特征方程:(\det(A - \lambda I) = 0)。
- 对角化 (Diagonalization)
- 条件:(A) 有 (n) 个线性无关的特征向量。
- 形式:(A = PDP^{-1}),其中 (D) 为特征值对角矩阵。
- 对称矩阵性质
- 特征值为实数,特征向量正交,可正交对角化((A = QDQ^T))。
六、正交性与投影
- 正交向量:(\mathbf{u} \cdot \mathbf{v} = 0)。
- 正交投影
- 向量 (\mathbf{b}) 到子空间 (W) 的投影:(\text{proj}_W \mathbf{b} = A(A^TA)^{-1}A^T \mathbf{b})((A) 的列是 (W) 的基)。
- 最小二乘法
- 解超定方程组:(A^TA\mathbf{x} = A^T\mathbf{b})。
七、相似矩阵与二次型
- 相似矩阵
- 定义:若存在可逆 (P) 使得 (B = P^{-1}AP),则 (A) 与 (B) 相似。
- 性质:相同特征值。
- 二次型 (Quadratic Form)
- 定义:(Q(\mathbf{x}) = \mathbf{x}^TA\mathbf{x})((A) 对称)。
- 主轴定理
- 通过正交变换 (\mathbf{x} = Q\mathbf{y}) 化二次型为标准形:(Q = \lambda_1 y_1^2 + \cdots + \lambda_n y_n^2)。
八、实用技巧与公式
- 行列式计算:
- (2\times2):(\det\begin{pmatrix} a & b \ c & d \end{pmatrix} = ad - bc)。
- (3\times3):沙路法(Sarrus)或余子式展开。
- 逆矩阵公式:
- (2\times2):(A^{-1} = \frac{1}{\det(A)} \begin{pmatrix} d & -b \ -c & a \end{pmatrix})。
- 快速求秩:阶梯形矩阵非零行数。
附:重要图示
- 行列式几何意义:线性变换后体积缩放比例。
- 特征向量方向:矩阵变换后方向不变的向量。
- 投影直观:向量在子空间上的“影子”。
学习建议:理解几何意义(如变换、投影),结合编程实践(NumPy/SciPy),并通过习题巩固概念应用(如解方程、对角化)。
此提纲覆盖线性代数核心框架,适合快速回顾或考前复习!
线性代数辅导讲义-硕士研究生辅导班专用
线性代数是全国硕士研究生招生考试数学考试中必考的内容,从历年考试的情况看,很多 考生对线性代数知识掌握得不太理想,甚至没有弄清楚其中很多基本原理
资料下载
![]() ah此生不换
2021-04-21 09:46:19
ah此生不换
2021-04-21 09:46:19
程序世界:线性代数是一种特定语言
、矩阵乘法等语义概念相应的语法编译/解释:SQL可以被编译/解释为C语言;线性代数相关概念和运算规则可以由初等数学知识来解释实现:我们可以在MySQL、Oracle等关系数据库上进行SQL编程;我们也
TensorFlow XLA加速线性代数编译器
加速线性代数器(Accelerated linear algebra,XLA)是线性代数领域的专用编译器。根据 https://www.tensorflow.org/performance/xla
线性代数是什么?为什么要有线性代数?
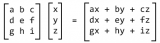
为什么要问这样一个看起来很蠢的问题呢?因为它的答案显而易见,大家对天天使用的程序语言的认识一定胜过抽象的线性代数,很显然程序语言虽然包含了 内在的逻辑,但它们本质上都是人为的设计。所有程序语言的共同性在于:建立了一套模型,定义了一套语法,并将每种语法映射到特定的语义。
2019-02-04 09:25:00
 换一换
换一换
- 如何分清usb-c和type-c的区别
- 中国芯片现状怎样?芯片发展分析
- vga接口接线图及vga接口定义
- 华为harmonyos是什么意思,看懂鸿蒙OS系统!
- 芯片的工作原理是什么?
- ssd是什么意思
- 什么是蓝牙?它的主要作用是什么?
- 汽车电子包含哪些领域?
- TWS蓝牙耳机是什么意思?你真的了解吗
- 什么是单片机?有什么用?
- 升压电路图汇总解析
- plc的工作原理是什么?
- 再次免费公开一肖一吗
- 充电桩一般是如何收费的?有哪些收费标准?
- ADC是什么?高精度ADC是什么意思?
- EDA是什么?有什么作用?
- 中科院研发成功2nm光刻机
- 苹果手机哪几个支持无线充电的?
- dtmb信号覆盖城市查询
- 怎样挑选路由器?
- 华为芯片为什么受制于美国?
- 元宇宙概念股龙头一览
- type-c四根线接法图解
- 锂电池和铅酸电池哪个好?
- 什么是场效应管?它的作用是什么?
- 如何进行编码器的正确接线?接线方法介绍
- 虚短与虚断的概念介绍及区别
- 晶振的作用是什么?
- 大疆无人机的价格贵吗?大约在什么价位?
- 苹果nfc功能怎么复制门禁卡
- 单片机和嵌入式的区别是什么
- amoled屏幕和oled区别
- 复位电路的原理及作用
- BLDC电机技术分析
- dsp是什么意思?有什么作用?
- 苹果无线充电器怎么使用?
- iphone13promax电池容量是多少毫安
- 芯片的组成材料有什么
- 特斯拉充电桩充电是如何收费的?收费标准是什么?
- 直流电机驱动电路及原理图
- 自举电路图
- 通讯隔离作用
- 苹果笔记本macbookpro18款与19款区别
- 新斯的指纹芯片供哪些客户
- 传感器常见类型有哪些?
- 伺服电机是如何进行工作的?它的原理是什么?
- 无人机价钱多少?为什么说无人机烧钱?
- 以太网VPN技术概述
- 手机nfc功能打开好还是关闭好
- 十大公认音质好的无线蓝牙耳机






