基于SOGI滤波器的单相锁频环仿真案例

曾经发过基于 SOGI 二阶积分器原理的的锁相环的实现和仿真模型，可见：《一种应用于三相电网的双 SOGI 锁相环实现方法和仿真》。但是基于 SOGI 的特性还可以实现锁频环，可以自动的适应电网频率变化，大大的提升了基于 SOGI 原理的锁相环的性能。

SOGI 仅在谐振频率中心才能是 0dB 增益，这意味着当电网频率改变，SOGI 滤波器的谐振中心频率没有改变时，会导致 SOGI 输出的正交波形与输入波形相比会失真，导致锁相不准确。因此为了解决这问题，就需要获取电网的频率变化信息，然后同步的调整 SOGI 滤波器的谐振中心频率，来实现最佳的锁相性能。

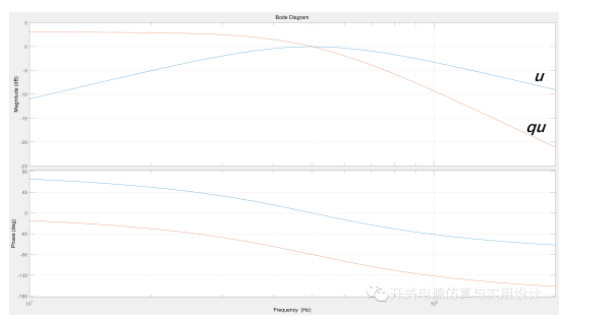
（SOGI 的频率响应）

观察二阶 SOGI 正交信号发生器，要使它能自动调节频率 wn，首先就是分析误差信号 e，并研究如何利用该误差信号来自动调节 SOGI 的谐振中心频率。

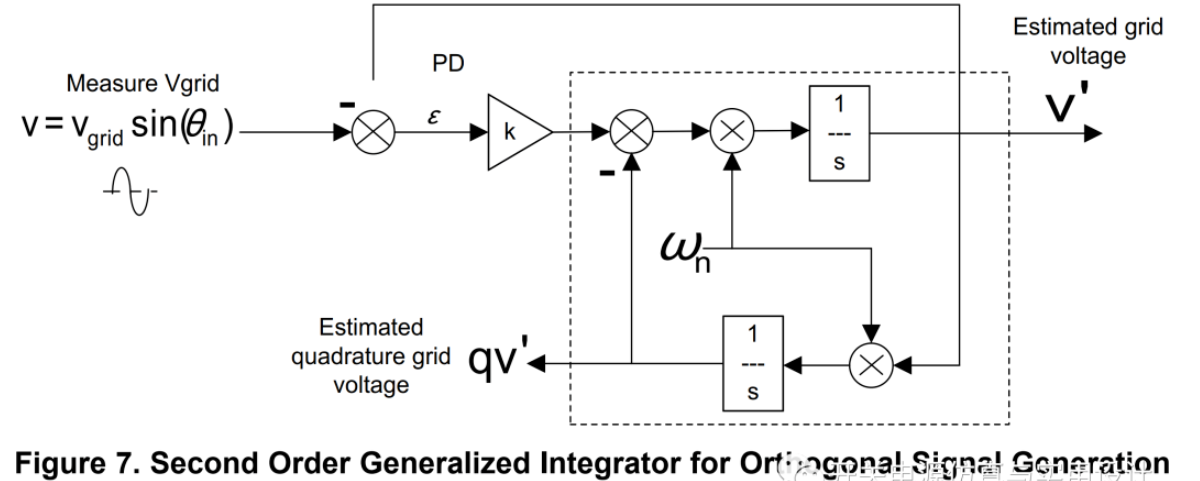
（SOGI）

从输入信号 v 到误差信号 e 的传递函数为：

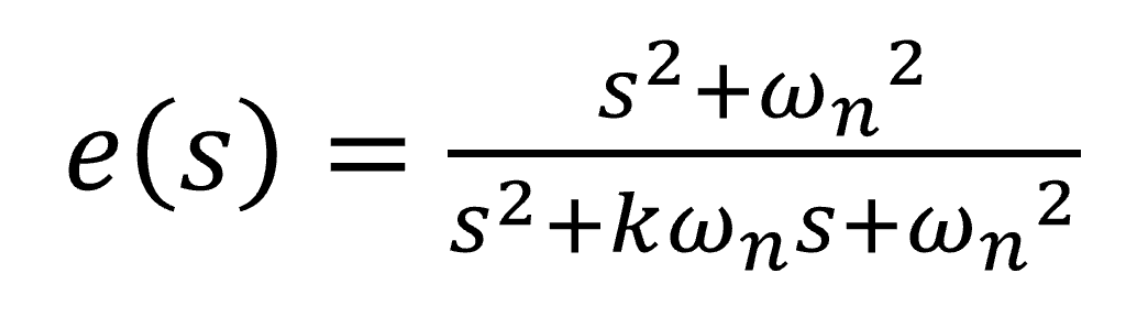
（误差信号传递函数）

这个误差的传递函数其实是一个二阶陷波滤波器，在其谐振中心频率出的增益为零。而且该传递函数还有个有趣的特征，当输入信号的频率 w 从比 SOGI 谐振中心频率 wn 低变为高时，输出信号的相角会发生 180°跳变，下面将用这个特性来比较两个频率的值。

为了研究 e(s)和 qu(s)之间的关系，下图把他们放在一起进行分析。可以看出当输入频率比 SOGI 的谐振中心频率wn低时，信号 e 和 qu 是同相的，反之，当输入频率高于 SOGI 的谐振中心频率 wn 时，信号 e 和 qu 是反相的。

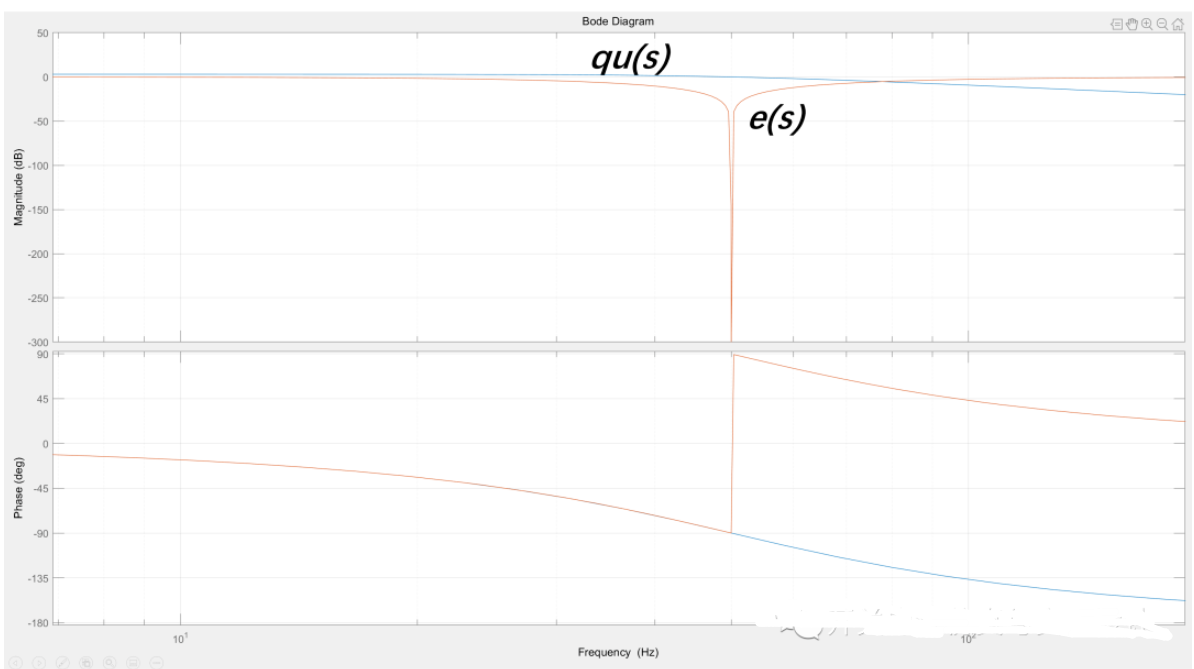
（误差信号传递函数的频率响应）

因此，频率误差变量 ef 可以定义为 qu 和 e 的乘积，正如上图看到的信息。当输入频率低于 wn 时，ef 的平均值大于零，两者相等时等于零，当输入频率高于 wn 时，该误差小于零。所以利用这特性可以设计一个非常简单的锁频环，可见下图：

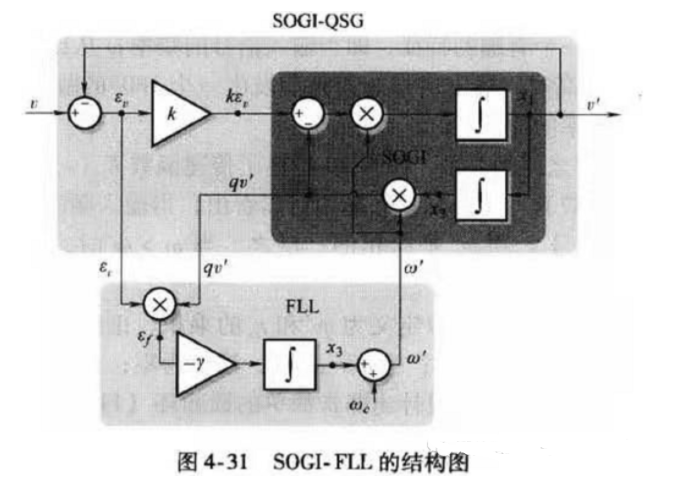
（SOGI FLL 结构）

在这个环路中，利用负向增益 r 的积分再加上电网频率的前馈使 SOGI 的谐振中心频率与输入频率一致，使 ef 的直流分量控制到零，实现锁频。因此可以将 SOGI PLL 和 FLL 结合起来，实现对电网频率扰动的自动补偿和跟踪，同步调整 SOGI 的谐振中心频率 wn，提升锁相的可靠性，可见仿真模型：

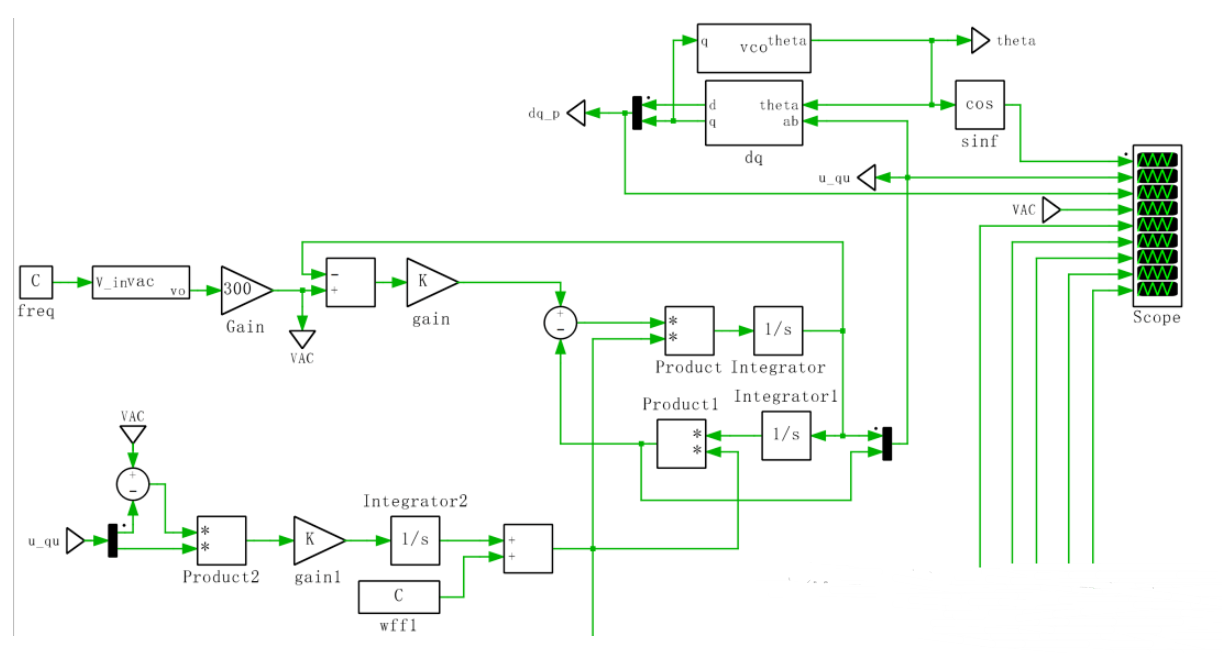
（SOGI FLL仿真模型）

运行测试，随意改变电网频率和幅值，锁相环都能快速锁相：

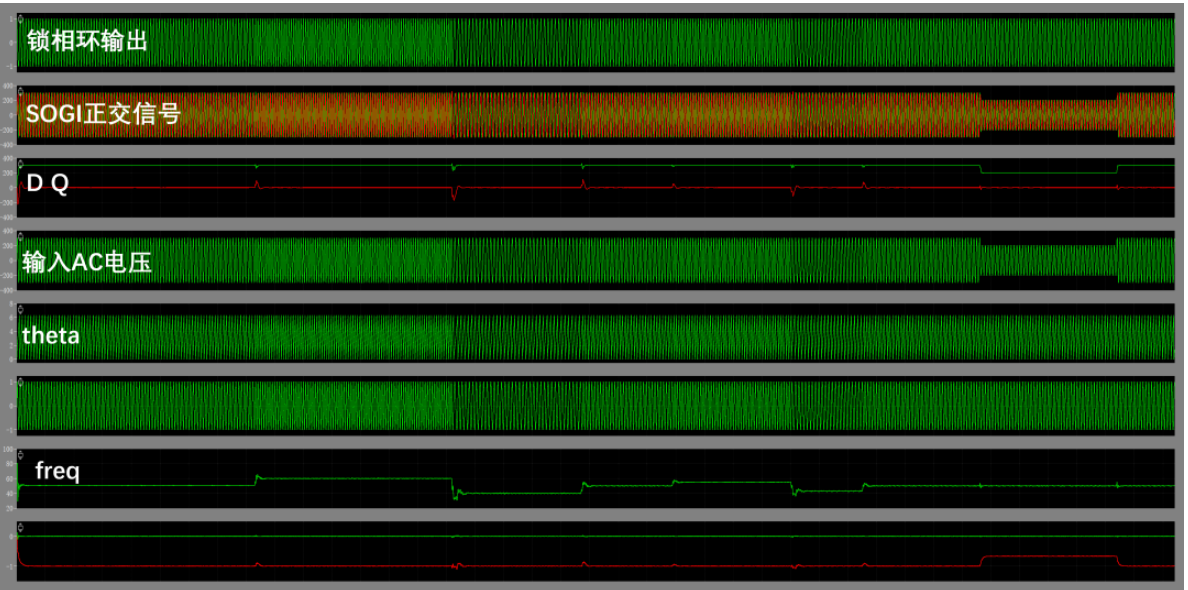
（SOGI FLL 在理想 AC 输入情况下仿真）

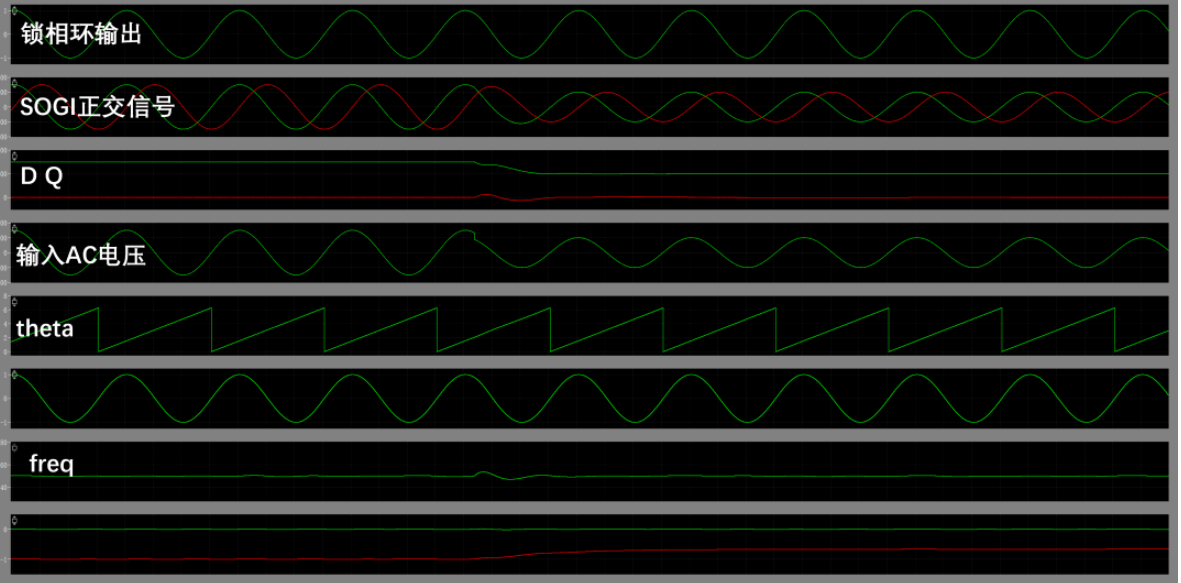
（SOGI FLL 在理想 AC 输入情况下仿真）

为了测试 SOGI 锁频环在电网高次谐波注入下的性能，我特别搭建了多次谐波注入的模型，可见，1~10 次随意改变：

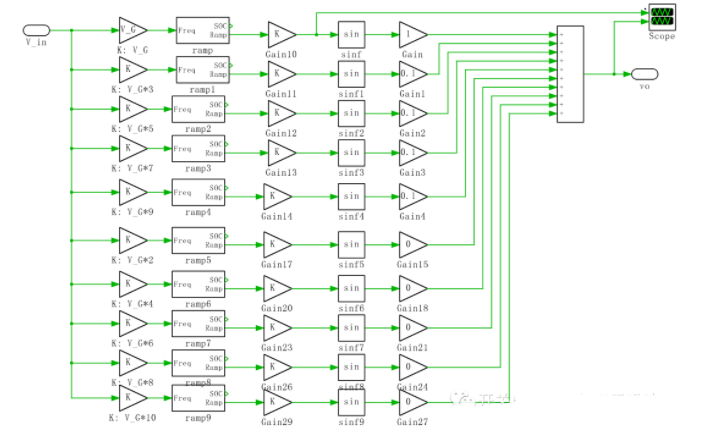
（谐波生成方法）

运行测试：即使在高次谐波注入情况下，SOGI 锁频环依然能很好稳定的锁相，性能确实不错：

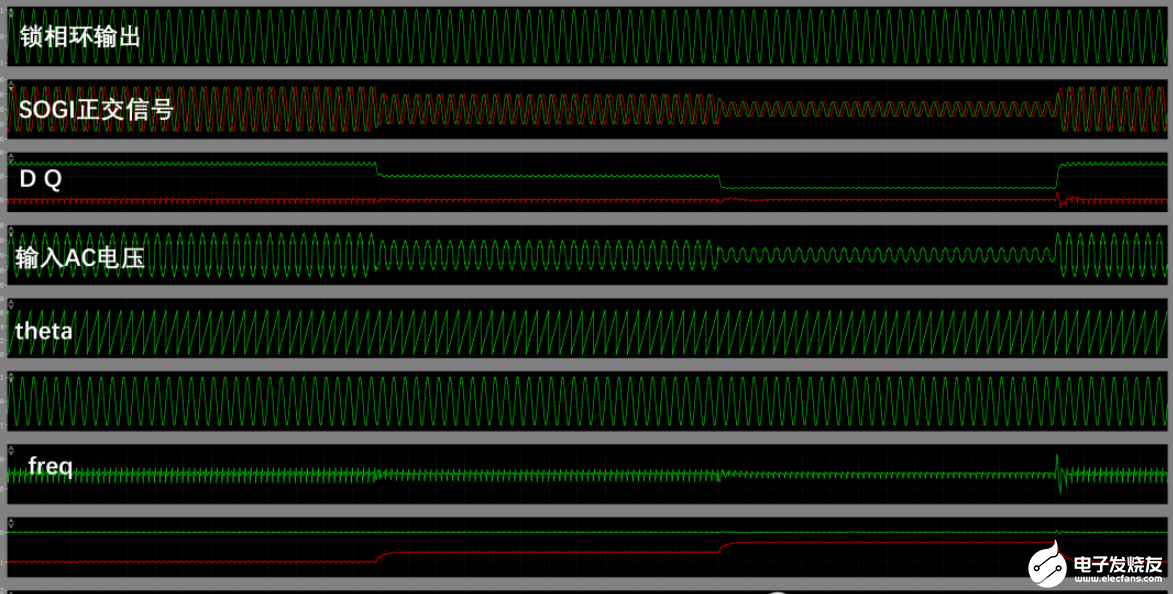
（SOGI FLL 在非理想 AC 输入情况下仿真）

（SOGI FLL 在非理想 AC 输入情况下仿真）

小结：参考书中 SOGI 锁频环的实现方法，搭建了单相 SOGI FLL 模型，并模拟电网存在高次谐波干扰下的锁频环性能，均达到了令人满意的效果。

参考文档：

1，光伏与风力发电系统并网逆变器

2，Software Phase Locked Loop Design Using C2000™
Microcontrollers for Single Phase Grid Connected Inverter -- SPRABT3A–July 2013–Revised July 2017
编辑：hfy