Johnson约翰逊计数器Verilog实现

 

问题：实现 N 位 Johnson Counter。

 

当 N = 4 时，输出应该是 

0000 -> 1000 -> 1100 -> 1110 -> 

1111 -> 0111 -> 0011 -> 0001 -> 

0000 -> ...

 

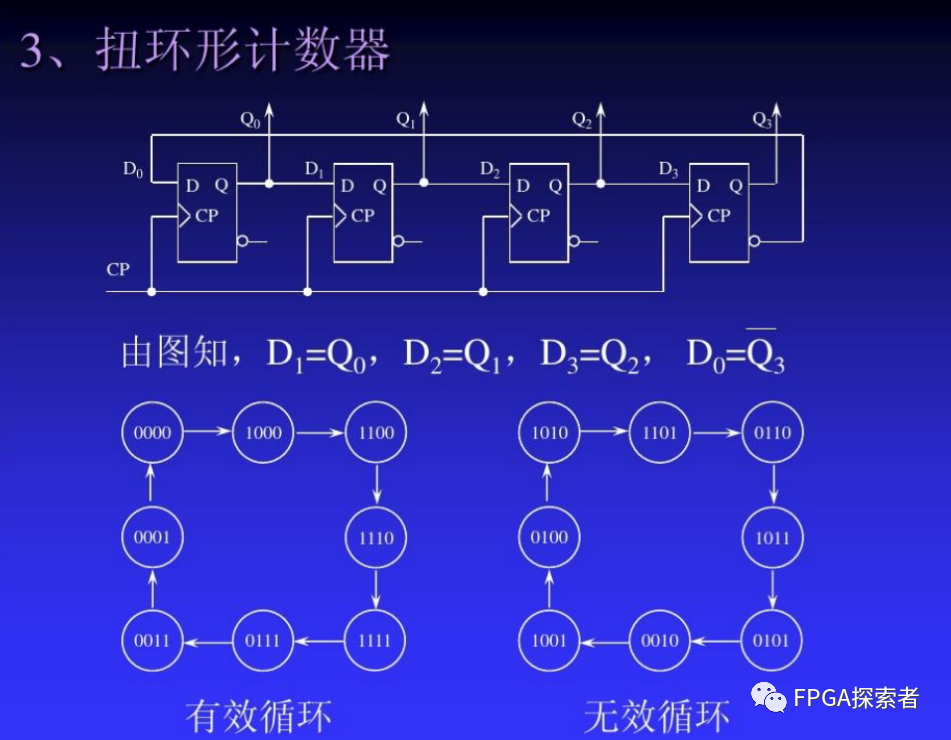
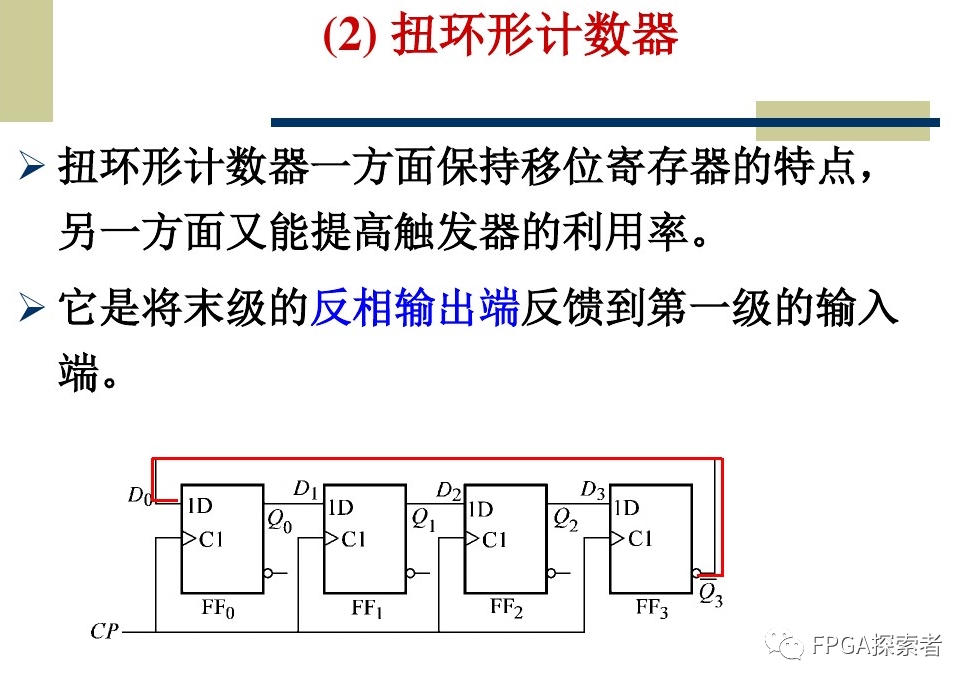
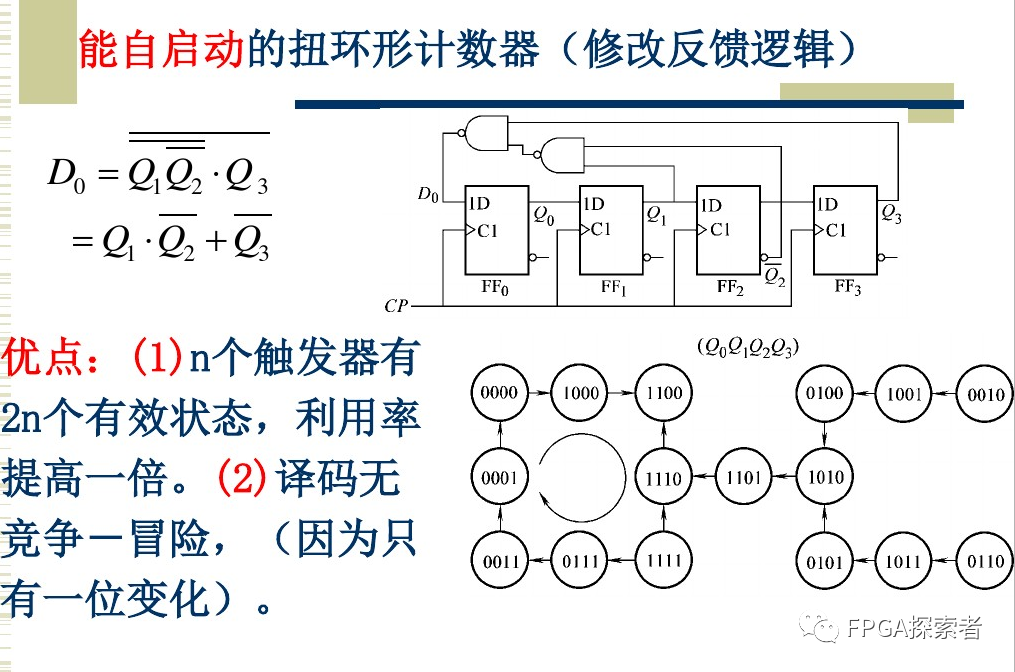
 如下图所示，扭环形（约翰逊）计数器最后一个触发器的输出取反 ~Q3，然后输入回第一个触发器的输入 D(0) = ~Q(N-1)，其余触发器的输入来自前级的输出 D(i+1) = Q(i)。

    D(0) = ~Q(N-1)

    D(i+1) = Q(i)

 

 

 

Johnson 约翰逊计数器Verilog 实现

 

用 Verilog HDL 写一个 8-bit 的 Johnson 计数器，N = 8。

module johnson#(      parameter N=8)(      input clk,      input rst_n,      output reg [N-1:0] q); 
always @ (posedge clk,negedge rst_n)begin    if(!rst_n)        q <= {N{1'b0}};        else if(!q[0])        q <= {1'b1,q[N-1:1]};    else        q <= {1'b0,q[N-1:1]};    endendmodule

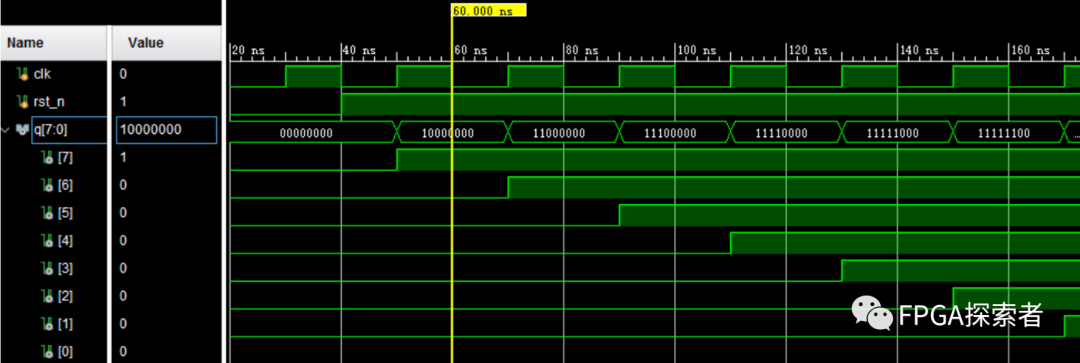
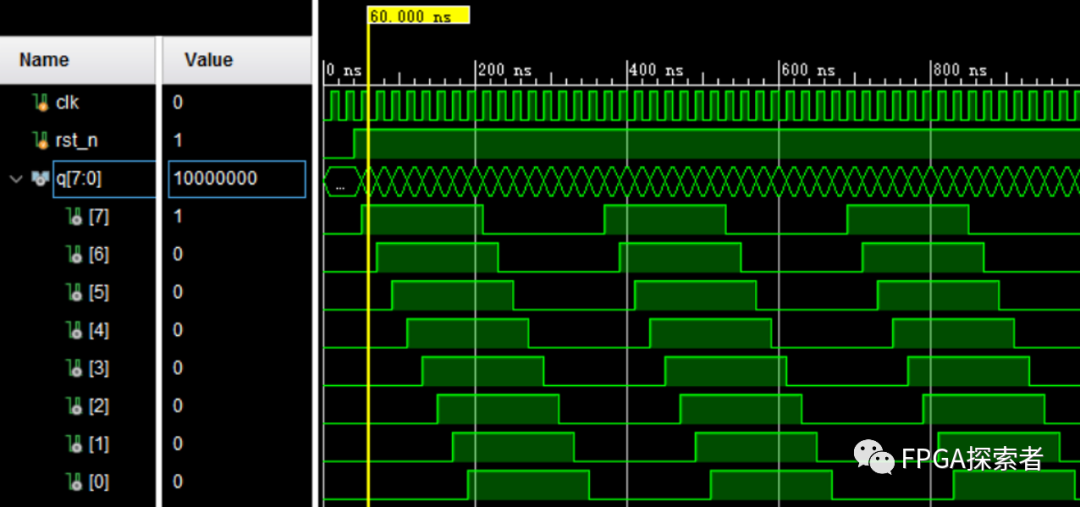
仿真图：

 

 

第二种：

module johnson#(      parameter N=8)(      input clk,      input rst_n,      output reg [N-1:0] q); 
always @ (posedge clk,negedge rst_n)begin    if(!rst_n)        q <= {N{1'b0}};        else        q <= {~q[0], q[N-1:1]};    endendmodule

 

Johnson 约翰逊计数器

 

 

（1）扭环形计数器，约翰逊计数器，每次状态变化时仅有一个触发器发生翻转，译码不存在竞争冒险，在n（n≥3）位计数器中，使用2n个状态，有2^n-2n个状态未使用；

（2）环形计数器，正常工作时所有触发器中只有一个是1（或0）状态，计n个数需要n个触发器，状态利用率低；

（3）n个寄存器的线性反馈移位寄存器LFSR可以产生的最长的随机序列是2^n−1长度(即m序列)。LFSR常被用来生成m序列，也可产生和校验 CRC。

 

 

 

 

审核编辑 ：李倩