

MOSFET的尺寸及伏安特性
模拟技术
描述
上期回顾
通过MOSFET器件结构的介绍和电学特性的分析,我们知道:
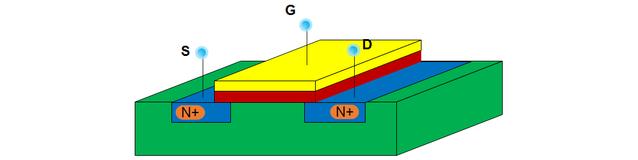
① MOSFET器件由导体-绝缘体-半导体三层结构组成。 导体的一端为栅极(G),P型半导体基板上两块重掺杂的N型半导体分别是源级(S)和漏极(D),具体哪一端是S,哪一端是D,需要通过其所接电压的大小才能确定。
② 直观的认识:当V_G>V_TH为常数时,沟道中的电流I_D随着V_D的增大而增大; 当V_D为常数时,沟道中的电流I_D随着V_G的增大而增大。
那具体I_D和V_G、V_D是什么关系呢? 表达式是什么? V-I特性曲线长什么样? :)OK,请往下看
全文内容:
MOSFET的尺寸
MOSFET的沟道的性质
MOSFET的伏安特性I
1、 MOSFET的尺寸
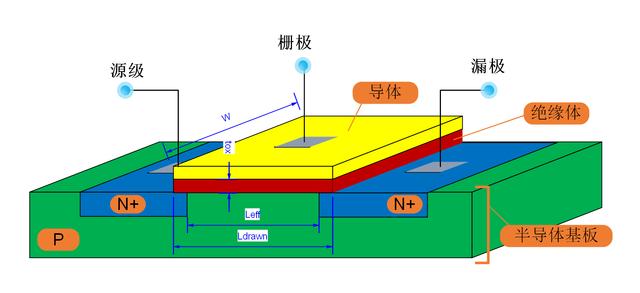
Fig. 2 MOSFET的几何尺寸
Fig. 2标出了我们所关注的MOSFET器件的几何尺寸,包括沟道的有效长度L_eff(导体的长度L_drawn略大于L_eff),沟道的宽度W,绝缘层的厚度t_ox,这些参数主要影响沟道两侧的电容和沟道的电阻,从而影响着电压电流的关系,后面的表达式会用到这些尺寸。
2、MOSFET的沟道的性质
因为流过沟道的电流I_D和沟道的性质强相关,所以要想弄清楚伏安特性,就必须先搞懂沟道的性质。
Case I:如图Fig.3 当V_G=1V,V_TH=0.5V,源级和漏极分别接地时,此时沟道打开,沟道中聚集了电荷。 但是沟道两头没有电压,就没有驱动力,此时I_D=0。
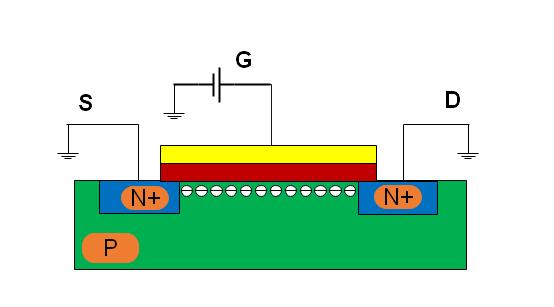
图3 案例I
Case II:如图Fig.4 所示,V_G=1V,V_TH=0.5V,半导体基板上的两级一个是0.6V,一个接地,因为N型半导体电压高的那端为漏极,低的一端为源级,所以V_D=0.6V,V_S=0V,得到V_GS=1V > V_TH,所以沟道开启。 因为V_DS=0.6V>0,所以沟道中存在从D流向S的电流。 (只要栅极相对于半导体基板其中任意一端的电压大于V_TH,则沟道开启) 。
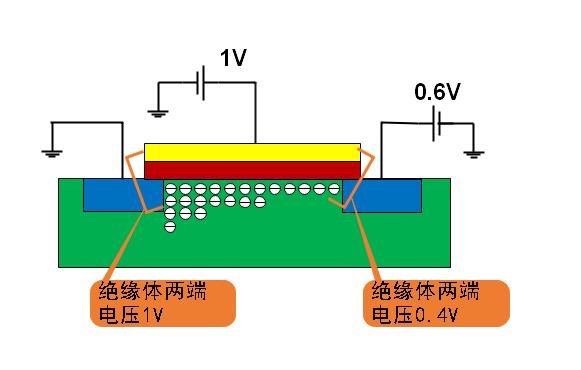
图4 案例二
但是因为源级和漏极电压不一样,沟道两侧的分布电压就不一样,靠近S端的电压为V_GS=1V,靠近D端的电压为V_GD=0.4V,根据Q=CV(一个圆等于两个半圆),沟道中聚集的电荷数量分布也不均匀。 靠近S端的沟道中电荷多,靠近D端的沟道中电荷少。
上面两个Case非常重要,这两个Case如果理解清楚了,就摸清了电荷在沟道中的分布规律,电荷的变化率就是电流。 根据上面的原理,我们来推导MOSFET的伏安特性。
3、MOSFET的伏安特性
①先搞清楚沟道的电荷密度分布
对于Case I,沟道中单位长度的电荷密度为:
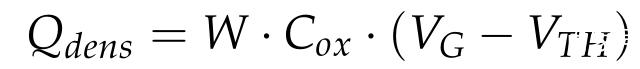
对于Case II,如图Fig. 5,沟道中单位长度的电荷密度为:
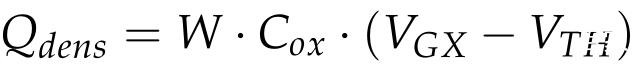
其中,C_ox为分别电容,表示沿着沟道每一点处的单位长度电容值,单位为F/m^2。 V_GX表示沟道每一点x处绝缘体上下两侧的电压差。
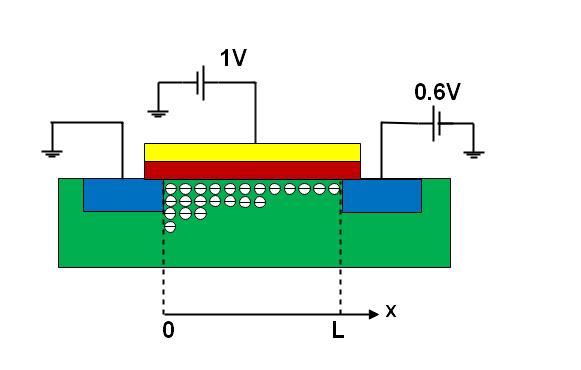
图5
② 根据电荷的分布求出I_D随电压变化的表达式
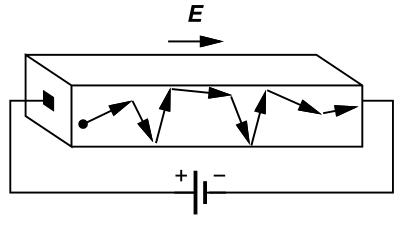
图 6
为了得到沟道中电流I_D的表达式,还有一个概念需要明确,即如Fig. 6所示,对一个物体两边加电压,物体中的自由电子就会加速移动,但是速度越快和周围物质的碰撞就会越频繁,使得速度不会一直增大下去,自由电子的速度会到达一定的数值就不会继续增加,但是这个速度值是和所加的电场成正比,即电场强度越大,自由电子最后稳定下来后的速度值也越大,可表示为
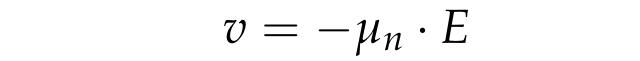
其中,u_n可以理解为电子的运动能力,所以

这些表达式看似复杂,其实思路很清晰,推导过程比较简单,红框内就是我们想要的表达式。 利用这个表达式,我们就可以知道I_D与V_GS的变化关系,I_D与V_DS的变化关系,这就是我们想要的,我们可以画出如下图的V-I曲线:
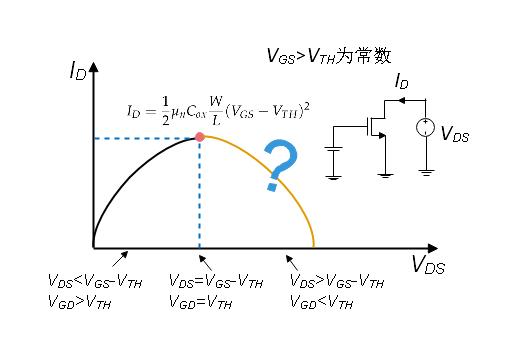
Fig.7 I_D随V_DS变化曲线
图Fig. 7为当V_GS为常数时,I_D随V_DS的变化曲线,按照红框里我们辛辛苦苦求出来的公式,当V_DS=V_GS-V_TH时,I_D取得最大值,当V_DS再变大时,I_D会减小。
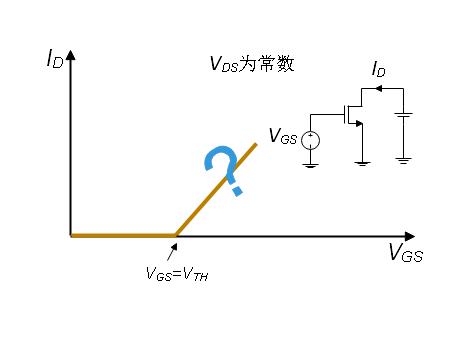
Fig. 8 I_D随V_GS变化曲线
图Fig. 8为当V_DS为常数时,I_D随V_GS的变化曲线,当V_GS小于V_TH时,沟道中没有足够多的自由电荷,沟道不能开启,当V_GS大于V_TH时,按照红框里的公式,I_D与V_GS为线性关系,沟道可以看成是一个恒定的电阻。
但是,有没有觉得得到的伏安特性曲线有些怪怪的? 我们辛辛苦苦求出来的公式有没有限制条件呢? 是不论V_GS和V_DS取任何值的时候都成立吗? 详情下回分解。
-
NPN型晶体管的伏安特性解析2023-02-20 3062
-
伏安特性曲线2024-12-10 664
-
元件伏安特性的测定2008-09-24 4990
-
伏安特性的测量2008-12-03 4301
-
基于三极管伏安特性的测量的LabVIEW程序2016-07-05 4514
-
伏安特性测试仪的测试范围2018-12-07 2207
-
电流互感器伏安特性试验2020-09-15 1972
-
压敏电阻的伏安特性2008-03-23 1899
-
元件伏安特性的测绘2008-11-02 18110
-
晶闸管的伏安特性是指什么2020-12-08 11841
-
晶闸管的伏安特性是什么?是怎样的?2022-09-29 4444
-
浅谈晶闸管伏安特性测试仪2023-04-20 1576
-
Multisim中虚拟伏安特性图示仪的使用2023-05-18 14227
-
LED的伏安特性 led的伏安特性曲线分为哪几个区域2023-11-30 9325
-
掺杂对PN结伏安特性的影响2024-07-25 5301
全部0条评论

快来发表一下你的评论吧 !

