数字信号处理的基础知识

写在前面

本文是本系列的第一篇，参考杜勇老师的数字滤波器MATLAB和Verilog实现以及一些网文博客，更新顺序参考杜勇老师的书籍目录。 本文主要介绍关于数字信号的一些基础知识。

固定点数

数字既包括整数，又包括小数，而小数的精度范围要比整数大得多，所以如果我们想在计算机中，既能表示整数，也能表示小数，关键就在于这个小数点如何表示。 于是人们想出一种方法，即 约定计算机中小数点的位置 ，且这个位置固定不变，小数点前、后的数字，分别用二进制表示，然后组合起来就可以把这个数字在计算机中存储起来，这种表示方式叫做「定点」表示法，用这种方法表示的数字叫做「定点数」。 也就是说「定」是指固定的意思，「点」是指小数点，小数点位置固定即定点数名字的由来。

在计算机中，通常将数据的小数点固定在数据的最高位之前或者最低位之后。 前者称为定点小数，后者称为定点整数。 定点小数 是纯小数，约定的小数点位置在符号位之后、有效数值部分最高位之前。 若数据 x 的形式为 x = x0.x1x2… xn ( 其中x0为符号位，x1～xn是数值的有效部分，也称为尾数， x1为最高有效位 )，则在计算机中的表示形式为：

在数字处理中，定点数通常把数限制-1~ 1之间，把小数点规定在符号位和数据位之间，而把整数位作为符号位，用0 、1表示正负，数本身只有小数部分，即尾数。 这是由于经过定点数的乘法后，所得的结果小数点位置不确定，除非两个乘数都是小数或者整数。 对于加法来说，小数点的位置是固定的，如上图x0位符号位，x1~xn为数据位。 在整个运算过程中，要求所有的运算结果的绝对值都不能超过1，否则会出现溢出。 在实际问题中，处理运算的中间过程会可能会出现结果超过1的情况，为了使得运算正确，通常会在运算时乘一个比例因子（类似归一化）避免发生溢出现象。

定点数的三种表示方法

定点带符号数在计算机内的四种表示方法是： 原码，补码，反码。 在FPGA处理中，比较都常用。

原码表示

最高位为符号位，0表示正数，1表示负数，其余位是数值位。 原码的优点是简单直观，特点是符号位与数值位在运算时要区别对待。 0的原码表示有两种形式。

反码表示

正数的反码表示与原码表示一样； 负数的反码表示为该负数对应的原码符号位不变，数值位按位取反。 因此，在反码表示中，最高位还是符号位，0表示正，1表示负，与原码相同。 0的反码表示也有两种形式。

补码表示

正数的补码表示与原码表示相同； 负数的补码表示是原码表示的符号位不变数值位取反，并在最低位加1。 补码中0的表示是唯一的。

浮点数

浮点数是一种公式化的表达方式，用来近似表示实数，并且可以在表达范围和表示精度之间进行权衡（因此被称为浮点数）。 在计算机中可以近似表达任意实数。 浮点数通常被表示为：A=M×B^E,B被称为阶码的基数，精度为N（使用多少位来进行存储），E在浮点数中表示为基的指数。 M被称为浮点数的尾数。

浮点显示方法

要表示浮点数，一是要给出尾数M的值，通常用定点小数形式表示，它决定了浮点数的表示精度，即可以给出的有效数字的位数。 二是要给出阶码，通常用定点整数形式表示，它指出的是小数点在数据中的位置，决定了浮点数的表示范围。 因此，在计算机中,浮点数通常被表示成如下格式:（假定为32位浮点数，基为2，其中最高位为符号位）

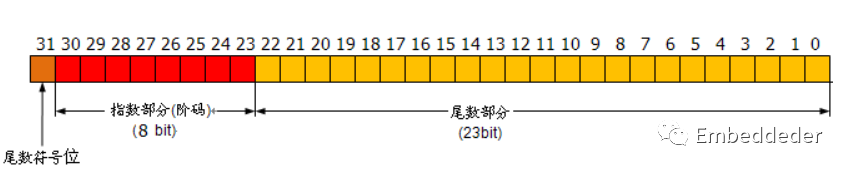
一种FPGA处理浮点数格式

虽然浮点数的表示范围更大，但实现时消耗的资源更多，实现的步骤也更加繁琐。 如浮点数的加法需要以下步骤：

1. 对阶操作：比较指数的大小，对指数小的操作数进行移位，完成尾数的对阶操作。
2. 尾数相加：对阶后的尾数进行加减操作。
3. 规格化：规格化有效位并根据移位方向和位数修改最终的阶数。

浮点数乘法操作，一般需要以下操作：

1. 指数相加：完成两个操作数的指数相加运算。
2. 尾数调整：将尾数M调整为1.M的补码格式。
3. 尾数相乘：完成讲个操作数的尾数相乘运算。
4. 规格化：根据尾数运算结果调整指数位，并对尾数进行舍入截位操作，规格化输出结果。

浮点数乘法器的运算速度主要由FPGA内部集成的硬件乘法器决定。 大部分FPGA芯片内部的乘法器为18bitX18bit。 这里以7系列的xilinx为例。 DSP48内部的乘法器为25X18的，如下图：

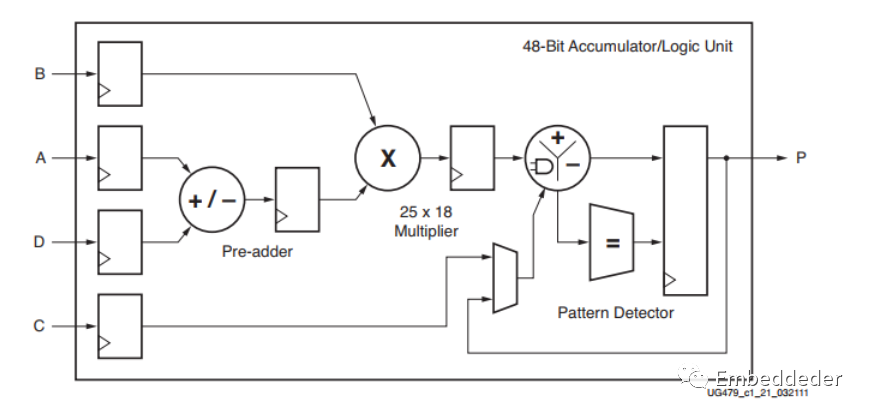
如果进行24位的乘法运算，则需要使用4个18bitX18bit乘法器，两个18位的数乘法操作只占用一个18bitX18bit乘法器。 由于FPGA的寄存器资源的设计，可以直接将尾数表示为补码的格式。 可以去除尾数调整的运算，减少一级流水操作。

杜勇老师在他的《多输入浮点加法器算法研究》中提出了一种新的浮点数结格式，也即一个26位宽的数，25--18位表示为8位有符号数，17--0表示为18位有符号的小数。 浮点数的表示式为M = f X 2^e;

规定，数值1的表示方法为指数为0，尾数为01_1111_1111_1111_1111；数值0表示为指数为-128，尾数为0。 这种自定义浮点数格式，相比24位的普通浮点数运算虽然精度有所下降但是可以大大节省乘法器的资源由是个乘法器变为1个，并有效地减少了运算步骤，提高了运算速率（由二级18X18乘法运算减少到一级运算）。

自定义浮点数和实数之间的关系：

FPGA中的运算

加减法运算

小数加减法运算

在Verilog中比较常用的数据类型是wire和reg以及他们的向量形式，在Verilog中，默认将所有的二进制数当做小数处理，也就是说小数点均在最低位的右边。 带小数的运算，设计者可以通过隐形规定进行，如，假设规定一个小数运算的小数点在最高位和次高位之间，然后进行小数的加减法运算。 和十进制的运算规则相同，在做加减法运算时，参与运算的两个数的小数点必须对齐，并且结果的小数点位置相同。

还有一种比较常用的处理办法是，将小数转换为整数进行运算，处理过程为同时把要运算的数进行乘一个很大的数如1024，即乘一个很大的整数处理掉小数部分，转化为整数，并约定该整数为之前的小数。 但是这样处理的弊端也比较明显，相比于直接进行隐形规定小数运算，会消耗更多的资源。

负数加减法

Verilog默认状态都表示的是无符号数，如果要指定某个数为有符号数，要在声明前加入关键字signed，如：wire signed [2:0] data; 这里表示data为3bit的有符号数，在运算时自动采用有符号运算。 下面引用杜勇老师书上的一个示例，并做略微改动。

有无符号数对比示例：

源文件：

`timescale 1ns / 1ps
module adder_test(
    data1,
    data2,
	sum_signed_out,
    sum_unsigned_out,
	compare_signed,
	compare_unsigned);

	input		[3:0]data1;              //输入加数1
	input		[3:0]data2;              //输入加数2
	output 	[3:0]	sum_unsigned_out;   //无符号加法输出
	outputsigned [3:0] sum_signed_out; //有符号加法输出

	output 	[3:0]	compare_signed;   //有符号数比较输出
	output 	[3:0]	compare_unsigned;   //无符号数比较输出
	//无符号加法运算
	assign sum_unsigned_out = data1 + data2;
	
	//有符号加法运算
	wiresigned [3:0] s_data1;
	wiresigned [3:0] s_data2;
	assign s_data1 = data1;
	assign s_data2 = data2;
	assign sum_signed_out = s_data1 + s_data2;

	//比较操作
    wiresigned [3:0] cons_1 = 4'b1001;
	assign compare_signed = (sum_signed_out < cons_1)? 1 : 0;
	assign compare_unsigned = (sum_unsigned_out < cons_1)? 1 : 0;

endmodule

测试文件：

`timescale 1ns / 1ps
module tb_adder();
    //输入
    reg  [3:0] data1;
    reg  [3:0] data2;
    //输出
    wire [3:0] sum_unsigned_out;    
    wire [3:0] sum_signed_out  ;
    wire compare_signed  ;
    wire compare_unsigned;
    //例化
    adder_test u_adder_test(
		.data1            (data1            ),
		.data2            (data2            ),
		.sum_unsigned_out (sum_unsigned_out ),
		.sum_signed_out   (sum_signed_out   ),
		.compare_signed   (compare_signed   ),
		.compare_unsigned (compare_unsigned )
	);
    //测试
    initialbegin
        data1 = 0;
        data2 = 0;
        repeat(16)begin
            data1 = data1 + 1;
            data2 = data2 + 1;
            #20;
        end
    end
endmodule

综合的RTL图：

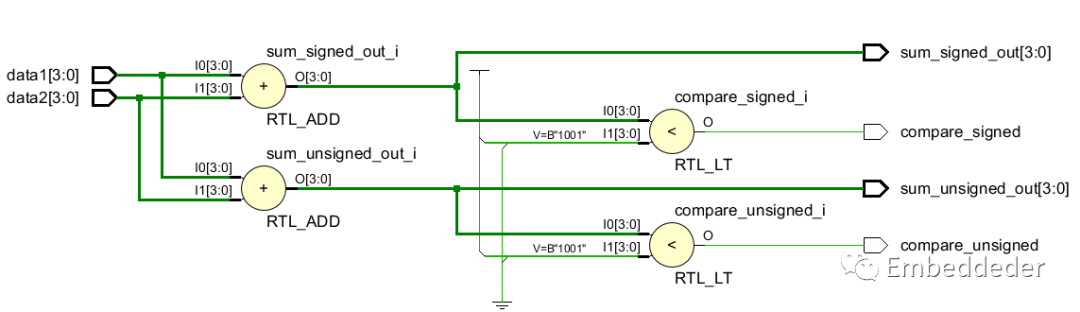
此时的仿真结果为下图：

通过对比可以知道，在进行运算时，有无符号数的运算结果在二进制中查看是相同的，但是表达的数值大小有区别，除此之外，有无符号数的区别也体现在比较运算上。

从下图中，可以看出，对于有无符号数来说，4‘b1001有符号数对应的是-7，无符号数对应的是9，所以两者的结果是不一样的。

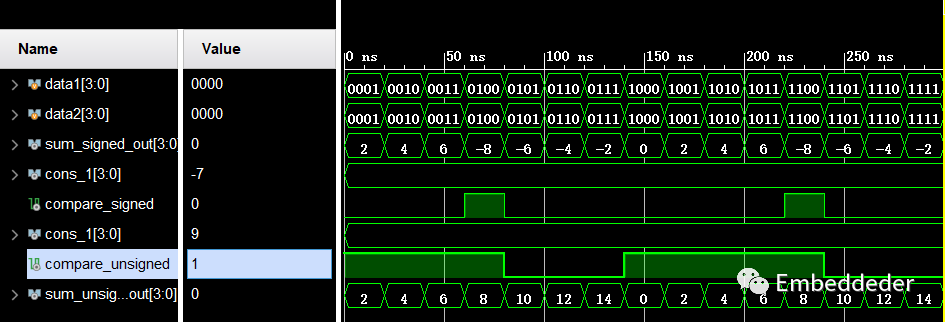
比较操作中为何不直接使用(sum_signed_out < 4'b1001)？

这里作为对比，将比较操作语句的cons_1直接改为4'b1001；

//比较操作
    //wire signed [3:0] cons_1 = 4'b1001;
	assign compare_signed = (sum_signed_out < 4'b1001)? 1 : 0;
	assign compare_unsigned = (sum_unsigned_out < 4'b1001)? 1 : 0;

在vivado的编译仿真器环境下输出结果如下:

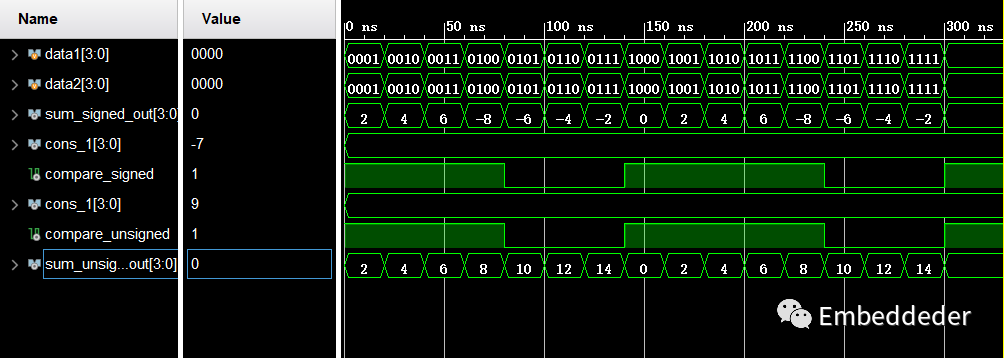
从波形可以看出，两个比较操作都是按照无符号数进行比较，这是因为在进行比较操作时，直接把比较数写入4'b1001，编译器会默认该数为无符号数，比较会按照无符号进行比较输出。 所以**有符号数进行比较时加上signed，即可考虑数值正负，完成正确比较,必须两个都要加signed，否则当作无符号进行比较。 否则只会将有符号数看作无符号数进行比较。 **

乘法运算

对于乘法运算，可以选择使用工具中自带的IP核，也可以使用基本的组件进行设计乘法电路。 相比加减法，乘法电路更消耗资源，一般情况下，对于信号和信号（数据）之间的运算，通常调用IP进行实现，而常数和信号直接的乘法运算，可以通过进行移位和加减法实现。 例如一个数乘2，等效为这个数左移一位； 一个数乘3等效为这个数左移一位+该数本身。

因为乘法运算的结果数据位数比乘数位数多，所以在实现乘法时，要先进行数据位数是扩展，以免出现数据溢出的现象。

除法运算

和乘法类似，可以选择使用工具中自带的IP核实现除法电路。 但是除法不可以在Verilog程序中进行直接实现，类比乘法电路的实现方法，可以将除法进行分解成若干右移的小项，然后进行加减运算操作。 例如一个数除以2，则可以将该数进行右移一位； 一个数除以3，可以将该数（记该数为A）近似分解 为，A右移2位+A右移4位+A右移6位。 （相当于该数乘了0.3281），因为该数是无限小数，所以对于分解法只能得到近似的结果，分解的项数越多，精度越高。 因为FPGA这些数字信号处理平台不可避免有限字长效应引起的。

有效数据位的计算

在FPGA中，所有的数据都是通过寄存器来存储，使用的寄存器越多，消耗的资源也就越多。 所以为了保证硬件资源的有效利用，需要精准掌握运算中的有效数据位的长度，尽可能的减少无效数据位参与运算，浪费资源。 有效数据位表示有用的数据位，例如数据范围为0-9，从寄存器的角度来说，只需要4个寄存器进行存储即可枚举所有0-9的状态，如果此时定义了5位的寄存器向量，那么多出来的那一位是无效的，任何时候都不代表任何信息。

加法运算的有效数据位

对于整数加法来说，假设加法中的两个加数最大的位数为N，则加法运算结果需要N+1位 才能保证结果不溢出。

对于小数加法来说，如果采用N+1位的数据表示运算结果，则小数点的位置在数据次高位的右边，如果采用N位数据表示运算结果，则小数点的位置在数据最高位的右边。 简而言之就是，小数部分的数据位数是不变的 。 为了确保得到N+1位的准确结果，要对参加运算的两个数进行一位符号位的拓展 。

乘法运算的有效数据位

对于数据长为M和N的数据进行乘法运算时，需要M+N位的数据才能得到准确的结果。 对于乘法运算当乘数为小数时，，不需要通过拓展位数类对齐乘数的小数点位置，乘法的结果的小数位数等于两个乘数的小数位数之和。 对乘法进行截取时，为了保证结果正确，只能取高位，舍弃低位。 只有在两个乘数均能表示最小负数时，才能拿出现最高位和次高位不同情况。 （最高位为1，其余为0），只有在这种情况下需要M+N位的数来存放结果，其他情况下，只需要M+N-1位来存放结果。

乘加法运算的有效数据位

在数字信号处理中，通常会遇到乘加运算的情况，一个典型的例子就是有限脉冲响应（Finite Impulse Response，FIR）滤波器的设计。 当乘法系数是常量时，最终运算结果的有效数据数据位根据常量的大小来重新计算。 假设乘加运算的变量输入是N位的数据，乘加运算的输出有效数据位计算如下：计算所有常数乘数绝对值之和SUM，算出SUM所占用的二进制数据位n，则乘加运算的输出的有效数据位数为N+n。

有限字长效应

数字信号处理的实质是一组数值运算，这些运算可以在计算机上用软件实现，也可以用专门的硬件实现。 无论哪种实现方式，数字信号处理系统的一些系数、信号序列的各个数值及运算结果都要以二进制形式存储在有限字长的存储单元中。 如果存储的是模拟信号，例如常用的采样信号处理系统，输入的模拟量经过采样和模数转换后，变成有限长的数字信号。 有限长的数就是有限精度的数。 因此，具体实现中往往难以保证原设计精度而产生误差，甚至导致错误的结果。 在数字系统中主要有三种因有限字长而引起误差的因素：

1. 模数转换器把模拟输入信号转换为数字信号时产生的量化效应
2. 把系数用有限位二进制表示时产生的量化效应
3. 数字运算过程中，为限制位数进行的位数处理和为防止溢出而压缩信号电平的有限字长效应

引起这些误差的根本原因在于寄存器（存储单元）的字长有限。 误差的特性与系统的类型、结构形式、数字的表示法、运算方式及字的长短有关。 在通用计算机上，字长较长，量化步很小，量化误差不大。 但在专用硬件，如FPGA，实现数字系统时，其字长较短，就必须考虑有限字长效应了。