

基于分段模型的CRM boost电路软开关时间优化设计
电子说
描述
临界导通模式(critical conduction mode,CRM)下的DC-DC变换器能够降低系统阶数,并且可以实现更高的效率而广泛应用于中小功率场景中 ^[1-3^ ^]^ .为了提高非同步boost转换器在CRM模式下的效率,一般考虑两种功耗来源,即导通损耗和开关损耗 ^[4-5^ ^]^ .导通损耗通过选用更低的导通阻抗的元器件来降低,而降低开关损耗则须要让开关在开启瞬间两端的电压最低来实现软开关 ^[6]^ .在boost转换器中,一般而言使用谷值开关(valley switching,VS)和零电压开关(zero-voltage switching,ZVS)来提高整体效率.
对于非同步拓扑,通常利用电感电流降到零后二极管的结电容Cj和MOSFET的输出电容Coss与电路电感的谐振,实现主开关管的VS/ZVS ^[7-8^ ^]^ .这两个电容均属于寄生电容,表现出对电压的强烈非线性关系.一般而言,普通硅基半导体寄生电容的非线性随电路状态(如温度、开关频率等)不同变化很大.相比之下,第三代半导体如基于氮化镓、碳化硅的半导体,因其宽禁带的特点,自身的各种特性对温度不敏感 ^[9-11^ ^]^ .这个特性为碳化硅(SiC)二极管结电容Cj以及氮化镓(GaN HEMT)输出电容Coss在实际工程中奠定了良好的应用基础.然而,开关元件参与谐振的寄生电容表现出对电压的强烈非线性,这让谐振过程难以直观地理解并计算.文献[12]为了简化该谐振过程,将寄生电容视为恒定的值.文献[13]将电容根据电压等级分为两段,方便了整体计算.文献[14]尽管考虑了不同的间隔来计算近似谐振时间,但是并未给出谐振特性的具体解释.这些文献没有给出足够精确的谐振特性,因而与实际谐振过程存在一定误差.
本研究通过对寄生电容的合理分段,提出了一个针对谐振情况下的分段等效电容模型,并基于此计算出了最优的VS/ZVS时间,根据此通过实验结果的对比充分证明了模型的有效性及计算时间的准确性.
1 适用于Boost电路VS/ZVS实现的等效电路分析
为了减小开关管的开通损耗,电路须要实现VS或者ZVS.在非同步整流的boost电路中,实现该功能是利用开关管的输出电容Coss 、二极管的结电容Cj与电路电感的谐振,适当设置MOSFET开通前的死区,让其开通瞬间两端电压最小.
图1所示为基于GaN的boost电路基本拓扑,图中:vin为输入电压;vo为输出电压;L为电路电感;Q为主开关管;D为二极管;C为电路输出电容;R为负载;iL为电感电流;vgs为开关管驱动电压;vds为开关管两端电压;vr为二极管两端电压;Coss为主开关管的寄生电容;Cj为二极管的寄生电容.
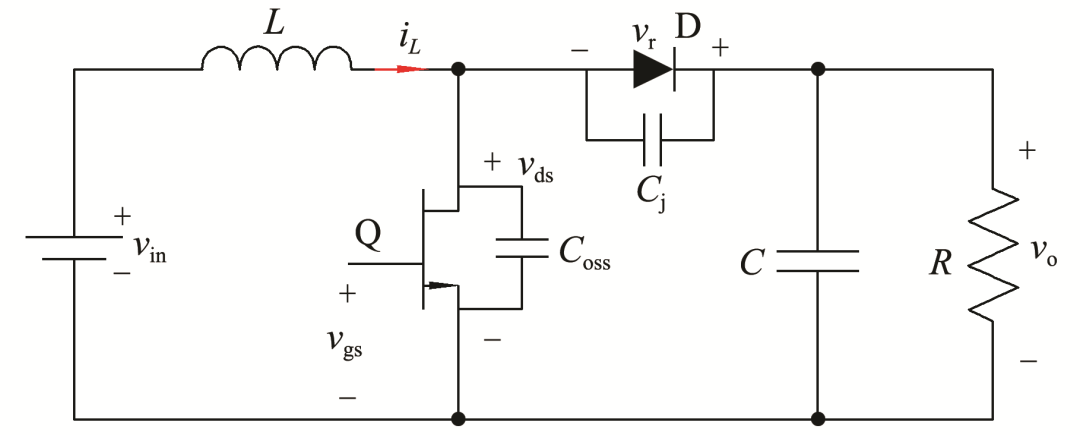
图1 基于GaN HENT的boost电路基本拓扑
由于VS情况可以看做ZVS情况下的延伸,因此下面以ZVS情况为例进行分析.图2所示为ZVS情况下boost电路在CRM模式下的电压电流波形,图中:Ton为主开关管开启时间;Toff为主开关管断开时间;tf为电感电流的下降时间.详细过程以时间段分开讨论.
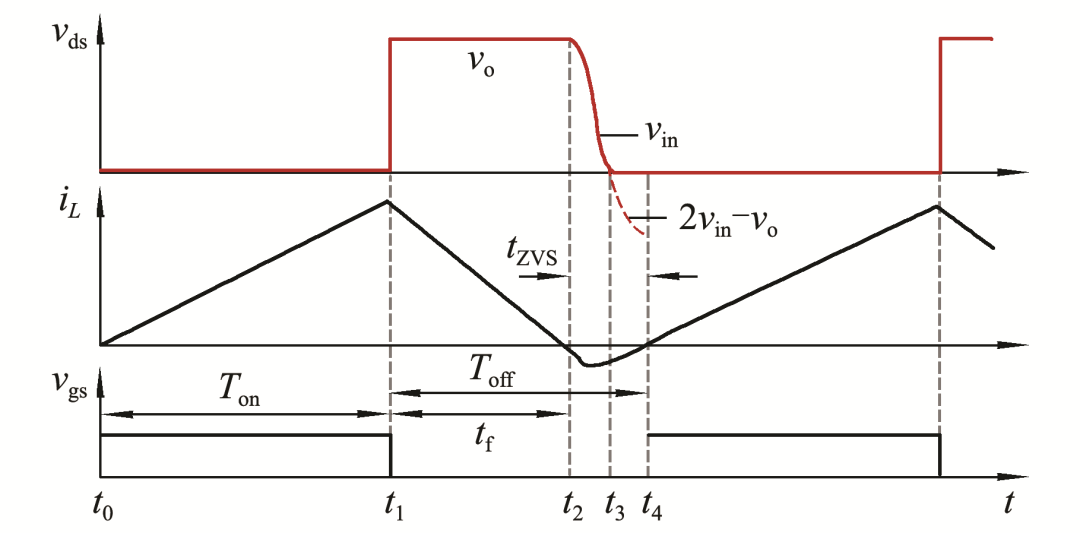
图2 boost电路在CRM模式下的电压电流波形
[t0 ,t1 )时间段:周期在t0时刻开始,开关管开启,vds =0,vr =vo ,电感电流在t0时刻从0开始上升.
[t1 ,t2 )时间段:t1时刻开关管关闭,vds =vo ,vr =0,电感电流在t2时刻下降至0.
[t2 ,t3 )时间段:二极管和主开关管均处于断开状态,Coss和Cj开始参与谐振.如图2所示ZVS情况下,t3时刻vds谐振值至0,iL谐振值未到0,但谐振过程结束.而VS情况作为ZVS的一种延伸情况,在t3时刻vds谐振值至最低点,iL谐振值至0,周期结束.
[t3 ,t4 ]时间段:针对零电压情况,主开关管反向导通,iL以 L /vin的速率在t4时刻上升至0,周期结束.
在以上的分析中,对于VS情况,考虑谐振过程最低点即可得到tvs的时间;对于ZVS情况,tzvs由谐振过程及电流回零过程组成,其中两者共同须要考虑的是谐振过程.
由于在实现VS/ZVS过程中电路的输出电容远大于两个寄生电容,因此该谐振过程基本拓扑可以等效为图3所示的谐振电路.
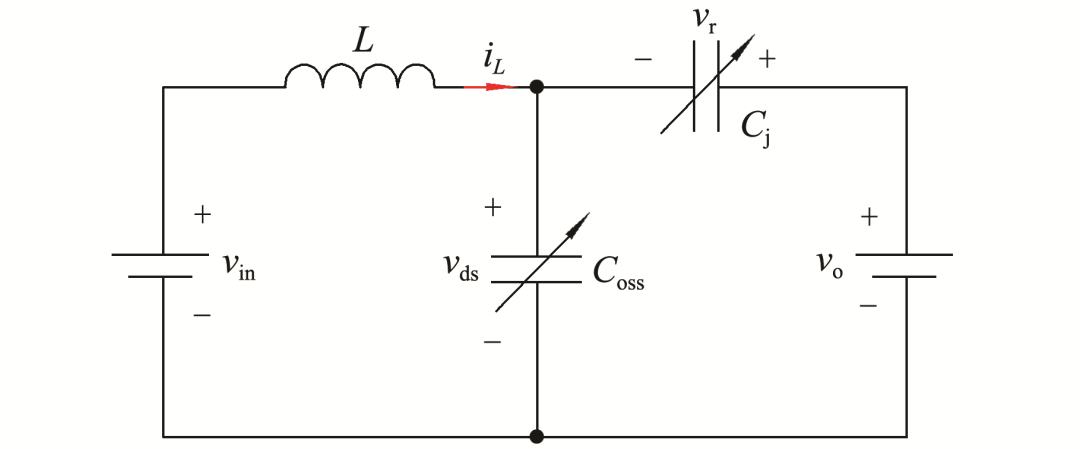
图3 实现VS/ZVS过程中的等效谐振电路
以t2时刻为起始时间点给出节点的电压电流微分方程为:
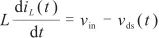 ; (1)
; (1)
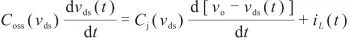 . (2)
. (2)
可以得到如下微分方程组
|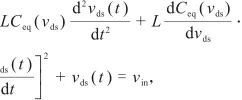 (3)
(3)
式中Ceq (vds ) C
Coss (vds )+Cj (vds ),其中Coss ,Cj与vds是强烈非线性关系,因此可以视为vds的函数.显然,式(3)是一个二阶非线性微分方程,其解析解很难求得.然而观察到:当左边第二项系数dCeq (vds )/dvds为零时,式(3)即可看做二阶线性微分方程,能够求得解析解.
以该方程为基础,本研究提出一种针对非线性电容的分段电容模型,基于该模型导出上述谐振过程的解析解,并求得实现boost电路CRM模式的最优VS/ZVS时间.
2 非线性电容的分段等效模型及VS/ZVS时间的求解
根据对式(3)所示的非线性微分方程的线性化,首先提出一种针对Coss和Cj在谐振过程中的分段等效电容模型,然后依据该模型给出计算谐振过程的基本计算方法.
2.1 分段等效电容模型
分段等效电容模型的建立主要是将非线性电容根据不同电压等级分段取等效恒定的值,以此建立分段等效电容模型.以vo 400 V为例,图4所示为适用于谐振状态下的分段等效电容模型示例.图 4(a)为C
400 V为例,图4所示为适用于谐振状态下的分段等效电容模型示例.图 4(a)为Coss及其分段等效值,其中:v5 =0 V,v1 =400 V,v4和v3为分段的电压边界;Coss,1 ,Coss,2和Coss,3为Coss被分段后每一段的等效值.图4(b)为Cj及其分段等效值,其中:v1 =400 V,v2为分段的电压边界;Cj,1和Cj,2为Cj被分段后每一段的等效值.
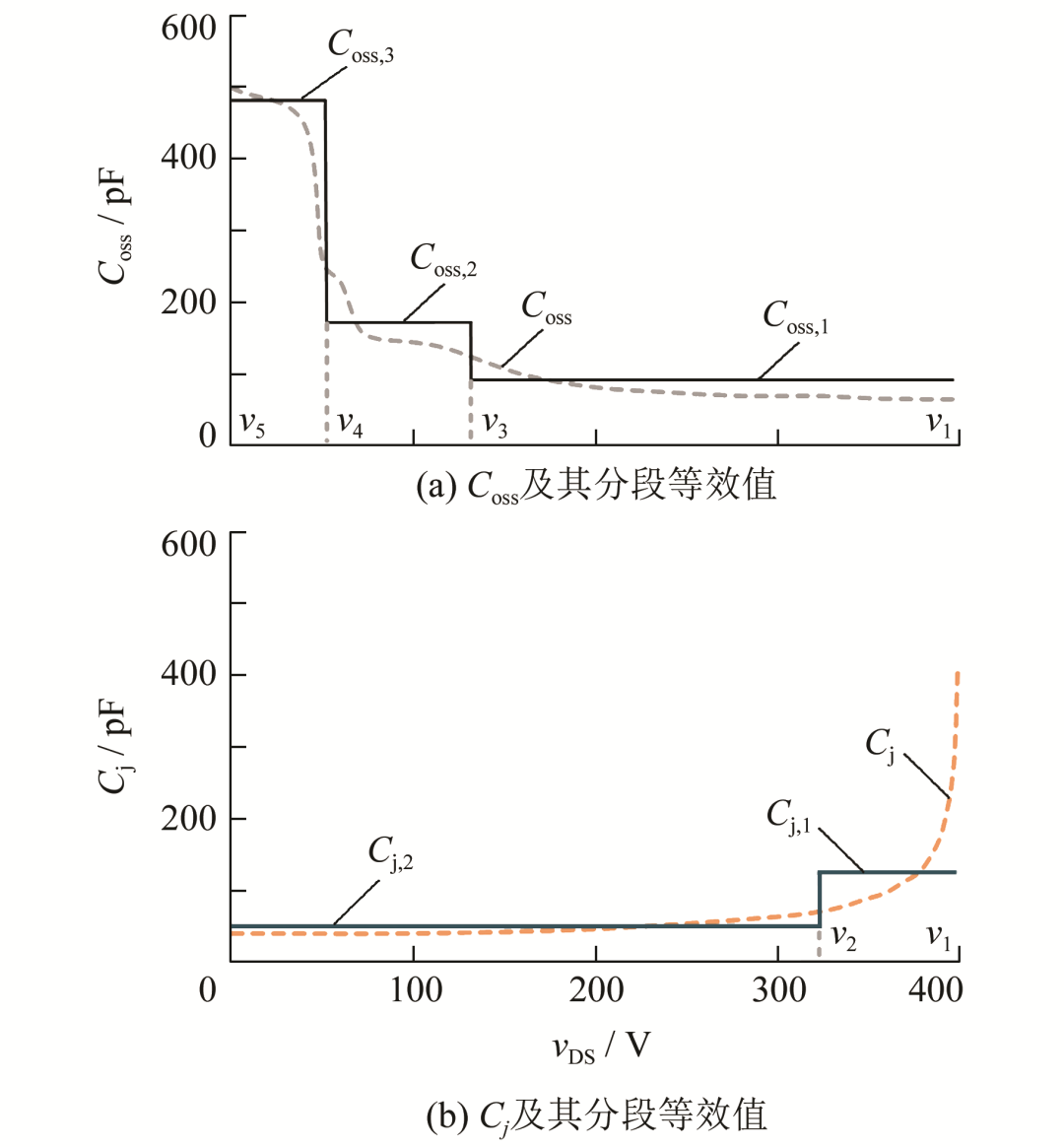
图4 当 v =400 V时适用于谐振状态下的分段等效电容模型
由图4可知:Coss被分为了三段,其中每一段的边界电压值v4和v3的选择让边界上的电容值满足Coss ( vn+1 )=2Coss ( vn ) ( n =3,4).相比较而言,当二极管两端的电压变高时,谐振后Cj (vds )迅速下降至较小值.由于在大多数情况下Cj比Coss小得多,因此可以将Cj (vds )分为两段,其中边界条件满足Cj (v2 )=2Cj (v5 ).
根据Ceq (vds )=Coss (vds )+Cj (vds ),将Coss与Cj的分段等效值叠加在一起,即可以得到一组不同电压范围下的等效电容值列表,如表1所示.
表1 不同电压范围下的等效电容值

2.2 分段电容值
根据分段等效电容模型建立的方式,为了计算谐振过程的解析解,通过基于电荷的等效方法获得每个间隔的等效电容,即计算每个间隔的平均电容.
对于边界电压为va和vb的区间,等效电容上的电荷QC满足
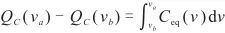 . (4)
. (4)
由于每个区间求得的电容值是一个常数,因此该区间的等效电容值为
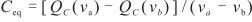 . (5)
. (5)
根据式(5)所示的计算方法得到每一段的等效电容值.
2.3 谐振过程的解析解及最优VS/ZVS时间
根据等效电容模型及其各个区间的初始条件得出谐振过程中vds和iL的解析解.下面首先描述解析解的求解方法,然后依据求得的解析解得到最优VS/ZVS时间.
为了更清晰地描述求解过程,将谐振过程依据电容等效模型的区间重新示意,如图5所示.其中谐振初始点在t1时刻,对应电压值v1 ,4个电容值区间的时间边界依次为t2 ,t3和t4 ,分别对应边界电压v2 ,v3和v4 .电压值在tzvs1时刻到0 V,电感电流在tzvs2时刻上升至0 A,为ZVS的最佳时间点.

图5 在ZVS情况下vds和iL的谐振波形
虽然电容值随电压变化,但是谐振结构在谐振期间保持不变,经过分段等效后电路的谐振结构保持不变,且依旧满足式(3).因为每一段的电容值是一个定值,所以非线性微分方程(3)可以转化为
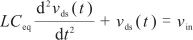 . (6)
. (6)
显然,式(6)是一个二阶线性微分方程,当vds >0时其通解为
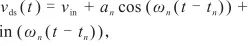 (7)
(7)
式中 (n
(n 1,2,3,4).将式(7)代入式(2)得到电流在谐振过程中的解析式为
1,2,3,4).将式(7)代入式(2)得到电流在谐振过程中的解析式为
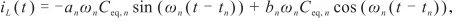 (8)
(8)
式中an和bn为常数,须要通过求解边界条件来确定,对于式(7),设t t
tn即可得到 ,b
,bn的求解则须要通过电流的边界条件给出.类似地,设t t
tn并对式(7)求时间t的微分,得到dvds ( tn )/dt b
bnωn ,则bn可以求得为
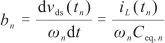 .
.
根据谐振过程中电压的解析式,可以通过迭代求得实现VS的时间点或实现ZVS的初始点tzvs1 .此后,电感电流将以vin /L的斜率上升到零,此时GaN HEMT反向导通,因此可得出最佳ZVS点即电感电流过零点tZVS2为
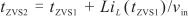 .
.
3 仿真和实验结果
为了验证非线性电容分段等效模型在计算VS/ZVS时间的时候的有效性,设计了一个输入电压范围为90240 V、输出电压为400 V、电感大小为54 μH、输出功率为200 W的CRM boost变换器.电路采用型号为GS66508T的GaN HEMT主开关管,型号为STPSC8H065的SiC主二极管,电路输出电容为2 μF,开关频率为250450 kHz.以下仿真数据基于实验所用器件的数据表.
3.1 仿真结果
图6(a)所示为基于分段等效模型tvs ,tzvs1和tzvs2随输入电压vin变化的曲线计算结果,其中输入电压vin的范围为90240 V.可以看到:tvs和tzvs2所示的曲面连续且光滑,说明计算结果符合逻辑规律.由于ZVS情况下电压第一次到0 V所需要的时间会减小,因此可以看到图中tzvs1~ <tzvs2一直成立.图6(b)所示为基于恒定电容模型的计算结果,可以看到结果与分段等效模型的结果相差较大,下面通过实验来验证.
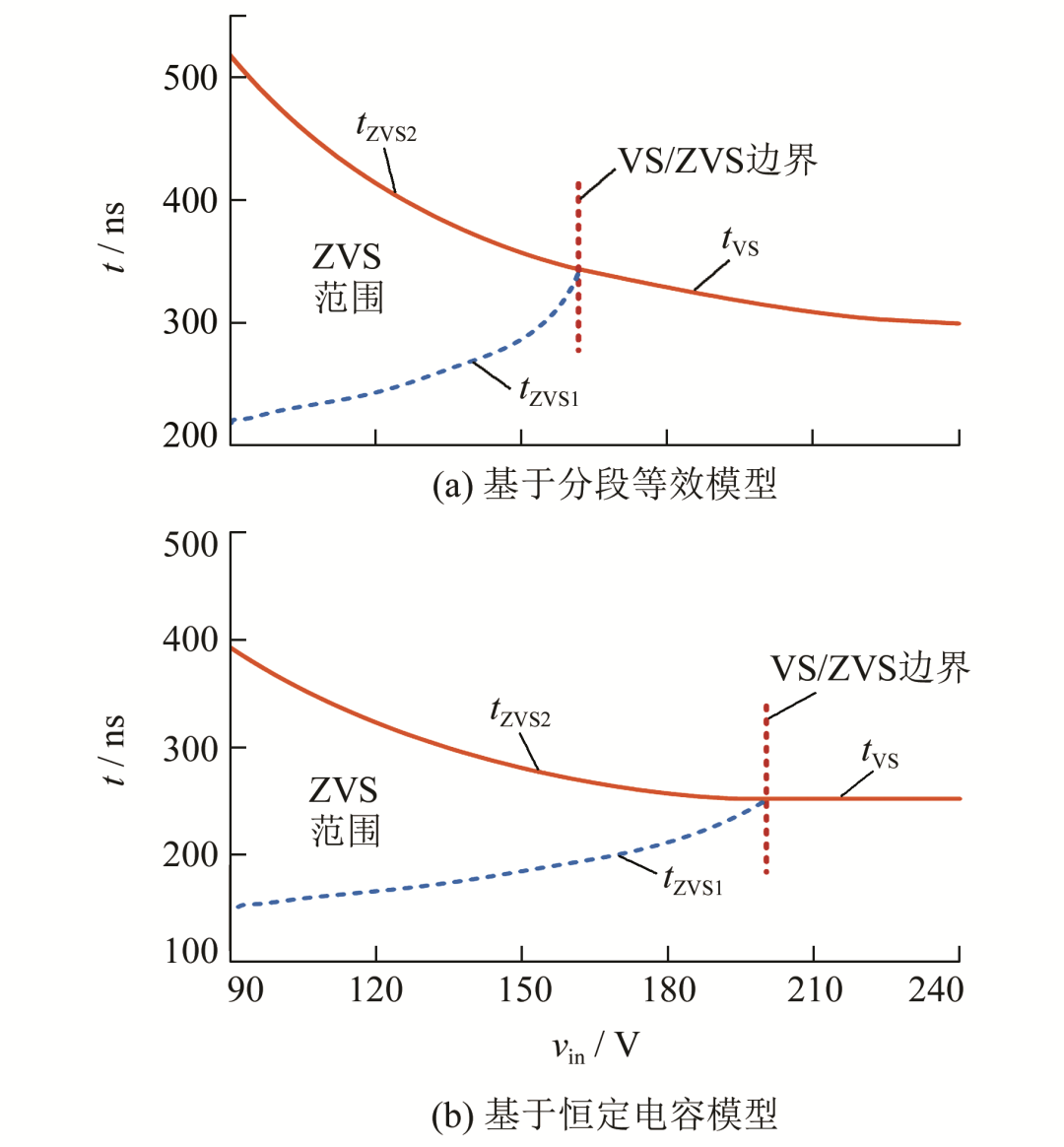
图6 随输入电压变化的VS/ZVS时间曲线
3.2 实验结果
分别在boost电路实现VS,ZVS及VS/ZVS边界的情况下验证基于分段等效电容模型计算得到的tvz /tzvs .
图7所示为CRM模式下boost电路中主要电压电流波形,由示波器存取波形数据绘制.图7(a)为实现VS时的电压电流波形,根据电流的过零点确定电压的谷值点,其中vin =200 V,tvs =320 ns,图6中相同条件下基于分段等效电容模型的时间为315 ns,误差为5 ns,相同条件下基于恒定电容模型的时间为252 ns,误差为68 ns;图7(b)为VS与ZVS边界时的电压电流波形,根据电流的过零点确定电压的谷值点,其中vin =165 V,tzvs =340 ns,图6中相同条件下基于分段等效电容模型的时间为342 ns,误差为2 ns,相同条件下基于恒定电容模型的时间为271 ns,误差为69 ns;图7(c)为实现ZVS时的电压电流波形,根据电流的过零点确定电压的谷值点,其中vin =135 V,tzvs =375 ns,图6中相同条件下基于分段等效电容模型的时间为380 ns,误差为5 ns,相同条件下基于恒定电容模型的时间为303 ns,误差为72 ns.
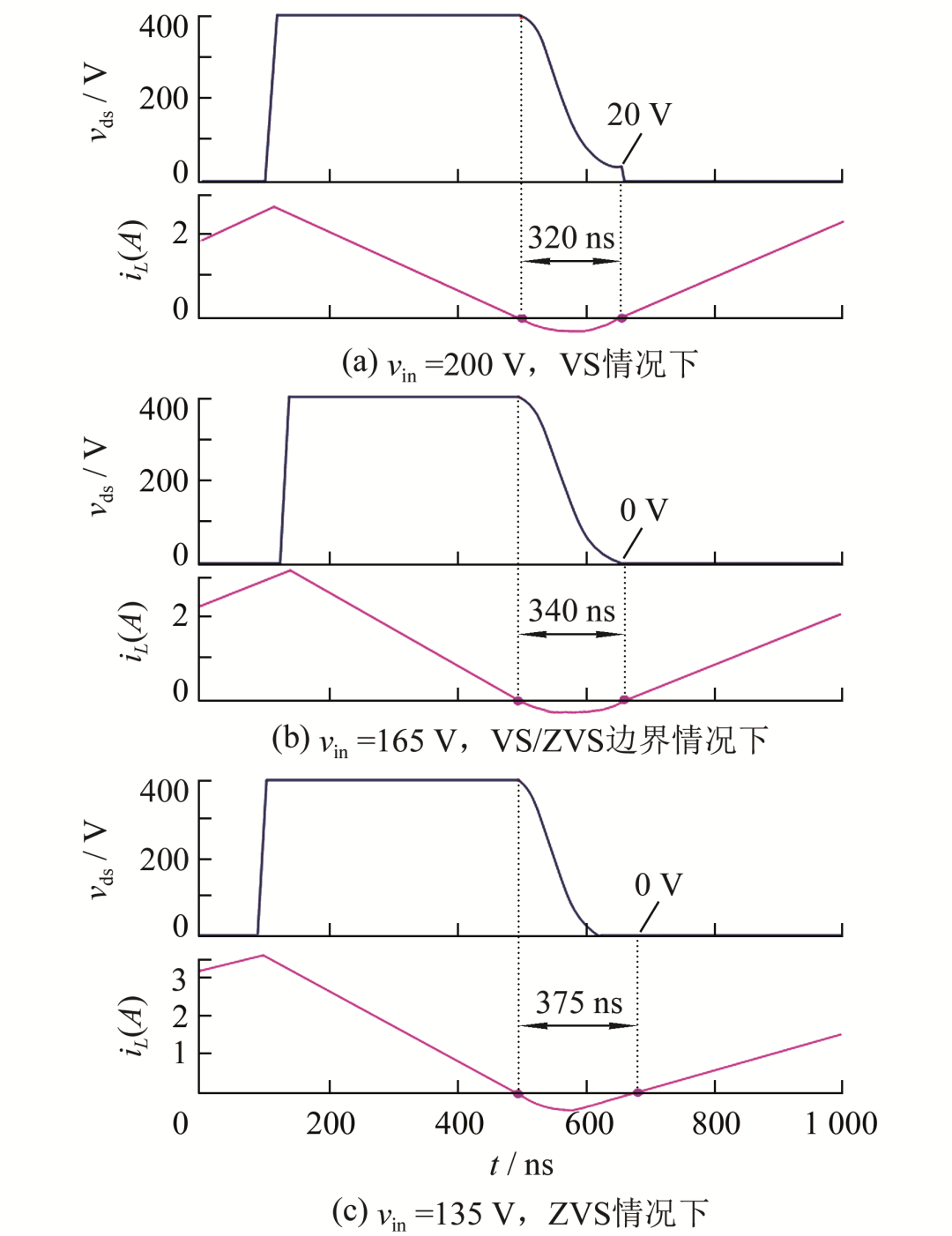
图7 CRM模式下boost电路中主要电压电流波形
以上实验中实现VS和ZVS的谐振时间与模型计算时间误差不超过5 ns,表明了模型及其计算结果的有效性.实验结果表明:利用所提出的分段等效电容模型计算的VS/ZVS时间足够准确,为实际VS和ZVS的实现提供了指导性的方法,并且为电力电子领域其他须要考虑非线性场合的计算提供了解决思路.
-
时控开关怎么调?时控开关怎么设置开关时间?2024-02-05 8610
-
交错CRM BOOST PFC仿真(2)2023-06-23 2731
-
晶体三极管的开关时间和测量2023-02-24 6480
-
中科软CRM系统排名_中科软CRM办公系统怎么选2022-03-21 577
-
求一个晶体管开关时间的测试搭建电路2020-03-05 2269
-
如何使用Boost电路实现软开关详细资料说明2019-12-18 3818
-
Boost PFC电路中开关器件的损耗分析与计算的详细资料说明2019-08-08 3359
-
MOSFET开关时间参数的重要性介绍2019-05-05 7105
-
无源软开关Boost电路图2019-04-26 2052
-
感应耦合电能传输系统软开关死区时间优化_蓝建宇2017-01-08 852
-
无源软开关BUCK、BOOST电路的研究2016-05-11 1151
-
Boost电路的一种软开关实现方法2009-07-11 9493
-
一种运用软开关的Boost电路2009-07-08 2928
全部0条评论

快来发表一下你的评论吧 !

