LDO的参数指标分析(1)

文章一开始介绍了LDO的历史和由来，以及为什么需要LDO这个东西。像在锁相环或者SAR ADC这样的系统里，由于不同模块的瞬态电流具有不同的频率分量，为防止模块之间的干扰，一般不会共享同一个电源。也就是说，每个模块需要一个单独的LDO。那么LDO的设计就显得尤为重要。

图一是一个基础的regulator的结构。其中pass transistor有两种选择，PMOS或者NMOS。前者是作为电流源的形式，后者是source follower输出。通常，我们将PMOS的regulator称为LDO。

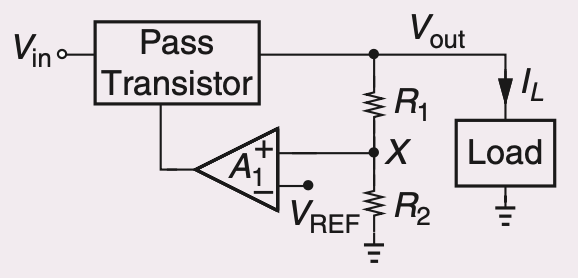
图一

除了dropout以外，无论哪种类型，需要关注的参数都是以下几点：

1. PSR ：Vin到Vout的增益，越小越好。来源有两条路，一是pass transistor，二是运放。
2. 输出噪声
3. load regulation ：负载电流变化引起的Vout变化，也就是IL到Vout的增益，和regulator输出阻抗直接相关。
4. 功耗和面积

原文是将这几个指标杂糅在一起讲的，本文希望按顺序逐个整理总结。出于篇幅考量，这里就只讲PSR，其余指标会在之后的文章中总结补充。

那么首先看一下PMOS作电流源的regulator，如图二。

图二

从运放输入正极断开，容易得出环路增益的表达式如下：

可以认为运放将M1的跨导等效增大了A1倍。

如何计算PSR呢？一个简单做法是将此结构简化为图三的形式，将电阻分压比直接乘到运放开环增益上，再推导Vin到Vout的传递函数。

图三

首先假设M1的ro1无穷大，那么Vin到Vout的前向通路表达式可以等效为一个共栅极放大器的增益，PSR可以直接写为：

分母刚好是1+ALG（分母第一个R2为笔误，应该是RL），分子则是前向通路的增益。容易看出， A1越大，电源抑制越好。 在ALG>>1的情况下，此式可以简化为：

考虑到主极点之后运放增益会衰减，高频下的PSR会随着运放增益的衰减而变差，如图四。

图四

因此，LDO需要一个高增益，大带宽的运放以获得较好的PSR。

另外一种做法是在输出端对地加一个大电容CM，那么表达式可重新推导为：

加电容后在输出端引入一个极点1/(RCM)，假设此极点高于运放主极点ω0，则图四曲线开始会在ω0处上升，在1/(RCM)后抑制上升趋势。高频下CM减小输出节点对地阻抗，从分压的角度也可以看出Vin到Vout的增益会减小。

另外单独考虑ro1对电源抑制的影响，此时忽略M1的受控源部分，那么PSR就是Rout和ro1的分压比，如图五。

图五

假设RL>>Rout，这部分的PSR表达式为：

Vout/Vin =Rout/(ro1 +Rout) =(1+R1/R2)/(gm1ro1A1 +1+R1/R2)

依然是A1越大越好，同时M1的本征增益也是越大越好。但由于这一部分PSR相比图三那一部分小了几乎是一个gm1*ro1倍，认为这一部分的贡献可以忽略。

讨论完M1的通路对PSR的贡献，另外考虑运放自身的PSR对系统PSR的影响。

图六

如图六，假设运放的供电和LDO主功率路径无关，运放电源的扰动为VnDD，此扰动到运放输出端的增益为β（也就是运放自身的PSR），我们可以很容易地推导出VnDD到Vn,out的表达式：

基本思路是从运放输出倒推到运放输入，再通过电阻分压推导至LDO输出。从表达式可以看出，想要弱化运放自身PSR对LDO整体PSR的贡献，需要尽可能地 增大A1，同时改善运放自身的PSR（减小β） 。这和我们之前的目标是一致的。

那么，如果运放的供电和LDO主功率路径是同一个电源呢？

图七

以图七为例，假如采用一个简单的NMOS输入的五管运放，DC情况下Mc的 VGS是一定的，因此Vin上的扰动会直接引起P点发生相同的变化，而稳定情况下VF又应该等于P点电压，因此五管运放的β=1，自身的PSR是很差的。但事实上，如果Vin的变化引起了VF有同样的变化，意味着M1的VGS趋于恒定，则LDO的输出电压更不容易受到Vin变化的影响，那么LDO整体的PSR反而更好。也就是说，在同一个电源供电下，五管运放PSR差的特点反而有助于改善LDO的PSR。

另外，拉扎维也提到一点，想要减轻运放自身PSR对LDO整体PSR的影响，有一种思路是用输出电压给运放供电。

分析完PMOS型的regulator之后，让我们来看一下NMOS型的regulator，如图八。

图八

如果不考虑M1的沟道长度调制效应，那么这种结构拥有完美的电源抑制能力，Vin到Vout的增益为0。

如果考虑M1的沟道长度调制效应，则按照前面的方法来分析，如图九。

图九

忽略M1的受控源部分，只考虑ro1和Rout的分压，可以得到表达式如下：

和PMOS型regulator相比，此时分母上多了gm1*ro1的系数，也就是减小了M1的本征增益倍。因此， 即便考虑非理想因素，NMOS型regulator依然有明显更好的PSR 。

对于regulator的PSR分析就到此结束啦，之后的文章里会补充LDO的其他指标分析，欲知后事如何，且听下回分解～