

功率系统中SiC MOSFET/Si IGBT栅极参数自动测试与计算新方案
模拟技术
描述
01
1.概述
随着“双碳”目标的提出,新能源领域得到快速发展。到2060年,预测中国风电和光伏发电装机容量占比之和需达到约80%,发电量占比之和达到约70%[1],电动汽车的保有量将达到约3.9亿辆[2]。SiC MOSFET和Si IGBT等功率半导体器件(以下统称器件),作为变流器的核心部件,得到大规模的应用。
器件的动态特性关系到系统的效率、可靠性和EMC性能,受到设计人员的重点关注。器件动态特性受到功率回路和栅极回路影响。功率回路特性依托于铜排结构(大功率器件)或PCB布局(板级器件),在定型后难以调整,修改周期长。栅极回路特性依托于PCB布局和栅极元器件参数,PCB上的元器件调整方便,所以设计人员主要通过栅极参数的调整来优化器件的动态特性。因此,栅极参数研究是器件动态特性研究的关键。
对于栅极参数的研究方法有两种:设计和测试。
栅极参数设计是通过理论计算或建模仿真,模拟器件的开关状态,掌握其动态特性。常用的仿真软件有ANSYS和MATLAB等,其核心还是理论计算。
器件动态特性测试一般通过双脉冲测试进行,根据测试结果来调整栅极参数,达到最佳效果。设计人员会应用专业的测试设备,保证测试结果的准确性和可靠性。Firstack开发的ME300D测试设备因此诞生。
设计和测试相辅相成,只有设计过程,会脱离物理世界环境,使得设计结果经不起实际工况挑战;只有测试过程,会让栅极参数优化周期漫长,测试人员通过不停试错才能获得满意的参数。
目前市面上的的动态测试设备通常都只停留在测试阶段。Firstack通过栅极参数匹配算法,加速测试过程。Firstack 开发的智能化测试设备ME400D将具备栅极参数自动计算匹配和自动化测试功能,目标提升客户测试效率。
本文对器件开关过程进行理论分析和计算,由于开关过程对称,以关断为例进行计算。MOSFET和IGBT关断过程基本类似,后续以MOSFET定义进行命名,部分IGBT相关图片,其C/G/E极分别对应D/G/S极。
02
2.关断过程研究
以MOSFET关断为例,栅极电压定义为Vgs。漏极电流定义为Id,Id的导通电流定义为ID,漏源电压定义为Vds,Vds的关断电压定义为VDS。如图1所示,将器件关断过程分为3部分,0~t2为第一阶段,该阶段Vgs下降到米勒平台,Id不发生变化,Vds缓慢增大,仍处于开通状态。t2~t3为第二阶段,该阶段处于米勒平台,Vgs维持米勒电压tm,Vds上升,基本达到VDS。其形成原理在此不做赘述。t3~t4为第三阶段,Vgs从米勒平台下降到阈值电压Vgs(th)。Id从ID下降到0。该阶段Vds会产生电压尖峰。
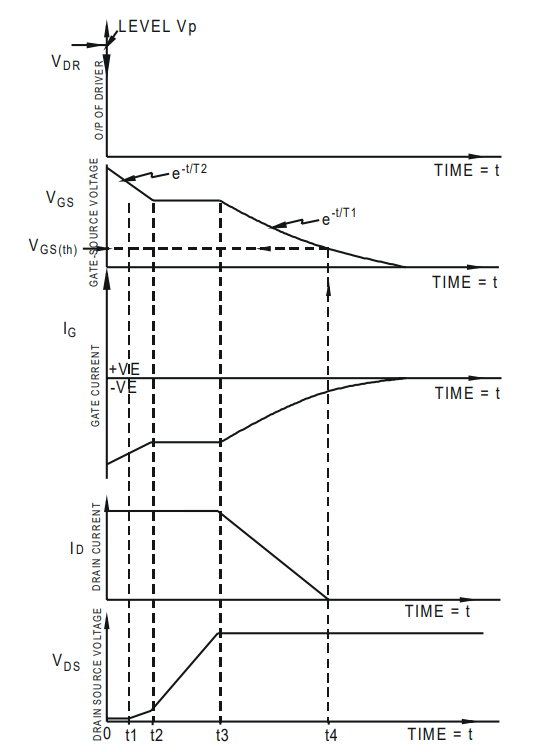
图1 MOSFET关断过程[3]
2.1 第一阶段
t0~t2阶段,驱动从器件栅极电容抽取电荷,此时的若不考虑栅极回路杂散电感的影响,可以看作一阶RC串联放电电路,Vgs从开通电压下降到米勒平台的时间tf1计算公式如下,
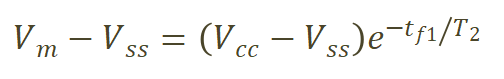
(1)
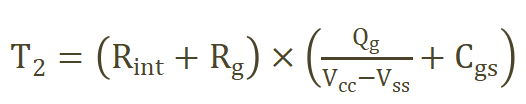
(2)
其中Vcc为驱动的开通电压,Vss为驱动的关断电压,数值为负,Rint为器件内部栅极电阻,Rg为外部栅极电阻,Cgs为栅极电容,Qg为器件对应Vcc和Vss之间的栅极电荷,如图2所示。Qg和Vds相关,通常规格书会给出典型Vds电压下的Qm,若测试工况和典型Vds电压相差较大,可能需要重新标定,我司自研了满足JEDEC标准[4]的Qg标定方案。
部分器件规格书会提供器件输入电容和反向传输电容,也可以通过电容进行计算,但如图3所示,容值会随Vds变化。特别在器件刚开始关断,Vds较小时,变化尤其明显,影响关断时间评估的准确性。用Qg计算等效栅极电容,会提高计算的准确度。
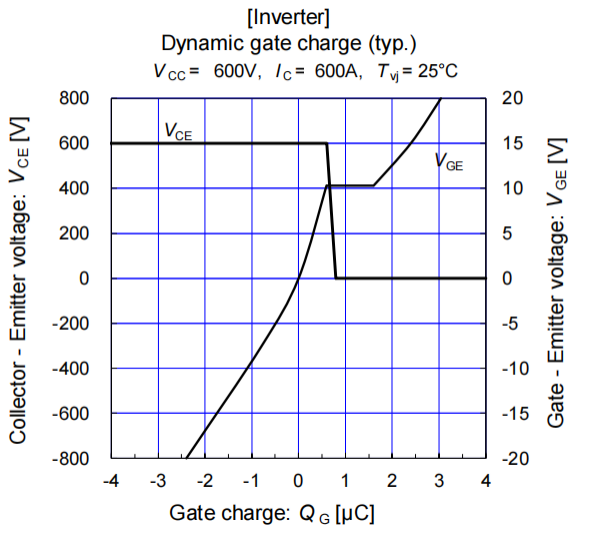
图2 规格书Qg曲线[5]
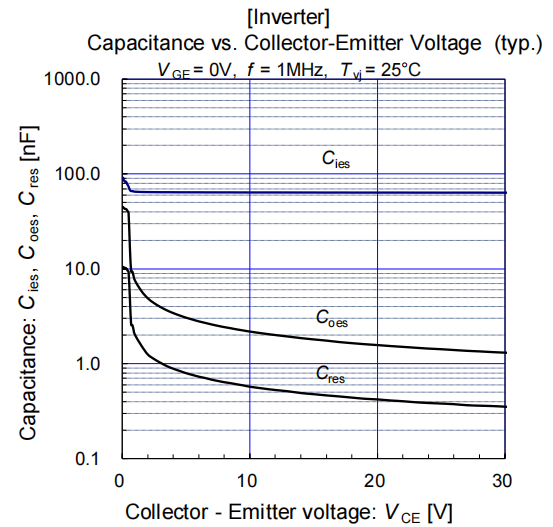
图3 规格书电容曲线[5]
2.2 第二阶段
2.2.1 米勒平台电压计算
米勒平台电压计算可分为两部分,当关断电流Id较大,对应传输特性曲线的Vgs电压远超过阈值电压Vgs(th)时,可认为器件的传输特性曲线处于线性区域[6],
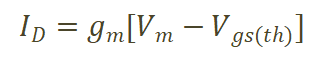
(3) gm为器件跨导,定义如图4所示。
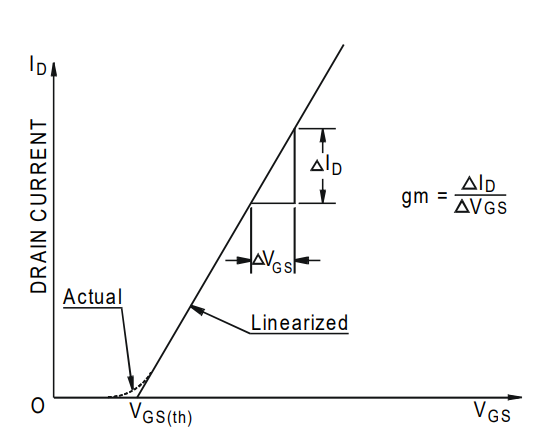
图4 跨导定义
当关断电流较小,对应Vgs接近阈值电压时,
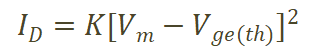
(4)
其中K是和温度相关的常数[7]。
若器件规格书给出详细的传输特性曲线,可以根据关断电流,在图5上取点来确认米勒平台电压。
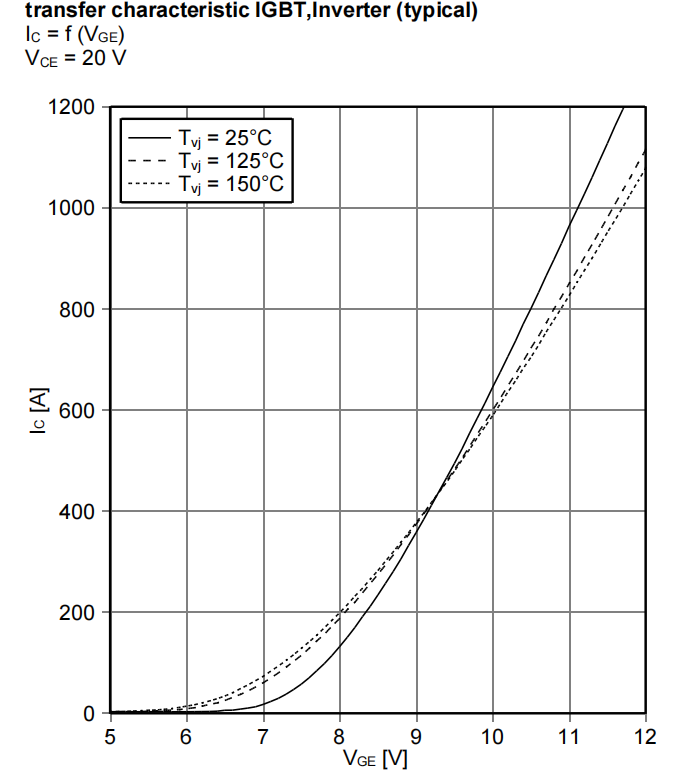
图5 规格书传输特性曲线[8]
对于Si IGBT而言,米勒平台电压基本保持不变,如图3所示。考虑到SiC MOSFET的短沟道效应,其漏极电压引起的沟道势垒降低(DIBL)效应明显,米勒平台应为图6所示的“米勒斜坡”[9],根据Qg曲线可以确定米勒平台中Vgs和Qg的变化关系。
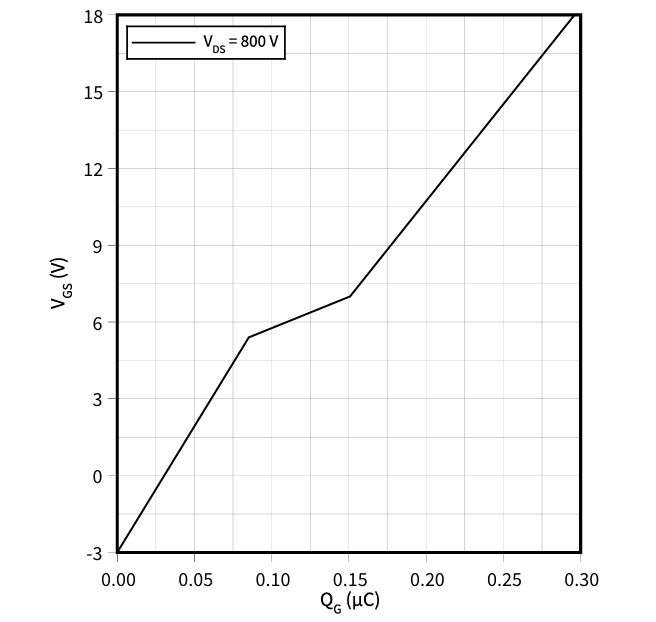
图6 SiC MOSFET的Qg曲线
2.2.2 米勒平台持续时间计算
当关断过程处于米勒平台阶段,驱动电流全部用作给米勒电容放电,栅极电压不变,驱动电流不变。器件在米勒平台时的驱动电流Igm和米勒平台持续时间tm计算公式如下。
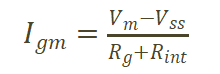
(5) 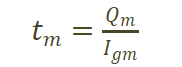 (6)
(6)
其中,Qm为图2中Vgs维持米勒平台时的电荷量变化值。
在米勒平台持续时间内,Vds电压会逐渐从器件导通电压上升到关断电压VDS。如图7所示,Vds往往是从米勒平台中段才快速上升,而非米勒平台开始时刻。Vds开始快速上升的时间tm2,在多级关断和主动控制型的驱动中有重要意义。由于米勒电容(即反向传输电容Crss)随Vds电压变化,该时刻点难以准确评估。本文给出一种近似评估方法。
以图3所示的1200V耐压器件为例。米勒电容在Vds小于30V时变化快。当Vds电压超过30V后,米勒电容基本发生变化,此时对应的米勒电容容值Cgd=Crss(Vds=30V),则
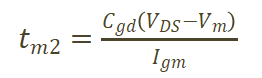
(7)
当Vds上升到VDS,米勒平台结束。
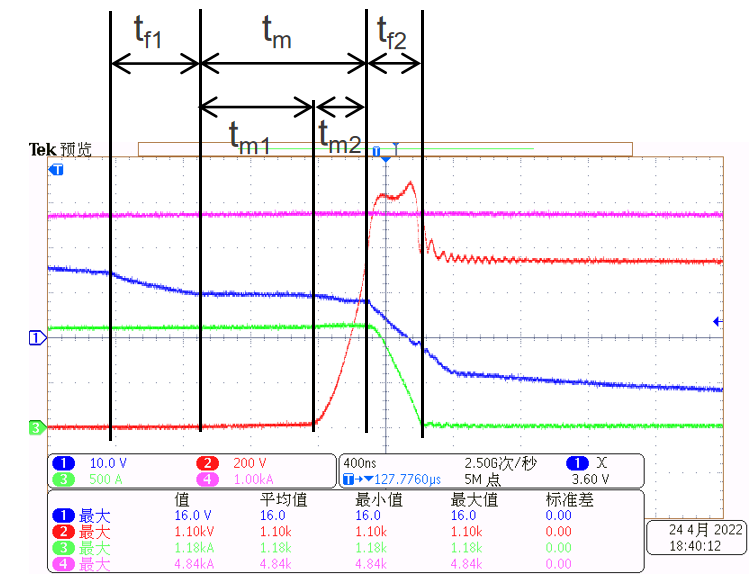
图7 器件实际关断过程波形(CH1:Vge,Vce, CH3:Ic)
2.3 第三阶段
t3~t4为Id电流下降阶段,当Vgs下降到Vgs(th),Id下降到0,关断过程基本结束。其电流计算方法与第一阶段类似,值得注意的是,此时Qg应按照Vm和Vss间的栅极电荷来计算。
通过tf2和ID可以计算出第三阶段电流下降阶段电流变化率,用ME400D设备进行双脉冲测试,可计算出功率模组的功率回路杂感Lp。从而得到电压尖峰
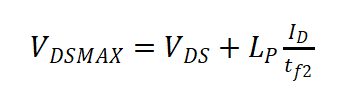
(8)
由于ID关断过程非完全线性,且SiC MOSFET第三阶段持续时间较短,容易造成偏差,通过该方法计算出的电压尖峰会有5~10%误差。
2.4 栅极回路电感对关断过程的影响
由于第二阶段驱动电流基本保持不变,杂散电感对此阶段没有影响,只需要关注第一阶段和第三阶段。
栅极回路电感由两部分组成,器件内部杂散电感和驱动PCB回路杂散电感。器件内部杂散电感较小,和外部杂散电感相比可以忽略。因此,可以将栅极回路等效成RLC串联电路。
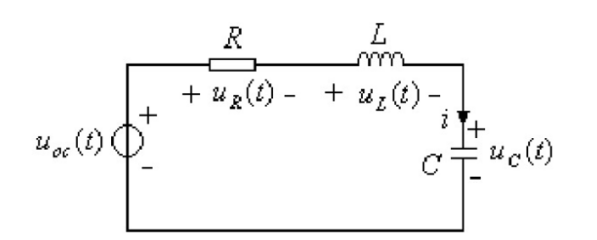
图8 栅极回路RLC串联等效电路
其完整的微分方程表达式为
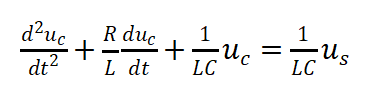
(9)
其初始状态
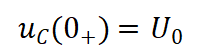
(10)
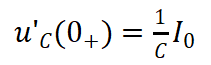
(11)
R为驱动电阻,L为栅极回路杂感,C为器件内外部GS电容之和,值得注意第一阶段和第三阶段C不相同,可以根据各自阶段的Qg和Vgs求出。
以图7电流方向为正。第一阶段,U0=VCC+VSS,I0=0,第三阶段U0=Vm+VSS,I0=-Igm。根据微分方程列出特征方程并求出特征根
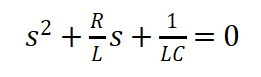
(12)
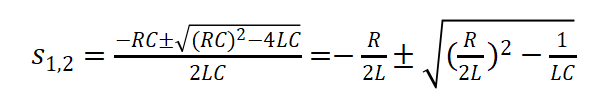
(13)
衰减常数
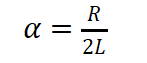 (14)
(14)
谐振角频率
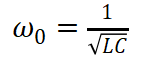 (15)
(15)
当α2 - ω02 >0特征方程有两个不等负实根,系统处于过阻尼状态。这种状态下,器件不会因为栅极形成振荡,驱动设计的关键之一,就是通过合理的驱动参数选择,使器件工作在该状态。
当α2 - ω02 =0特征方程有两个相等负实根,系统处于临界阻尼状态。
当α2 - ω02 <0特征方程有一对共轭复根,系统处于欠阻尼状态。这是驱动设计中需要避免的情况,会导致栅极振荡。对于SiC MOSFET而言,栅极电荷较小,对应C偏小,当L过大时,容易形成欠阻尼状态,这也是SiC MOSFET对栅极回路杂感更加敏感的原因。
通过特征根得出微分方程通解
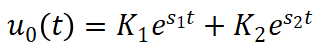
(16)
带入初始状态(10)(11),可分别求出两个阶段的K1和K2。
此时就可以得出第一阶段和第三阶段的响应方程,第一阶段最终状态为米勒平台,带入U0=Vm+VSS,即可求出第一阶段持续时间tf1。同理第三阶段最终状态U0=Vgs(th)+VSS,可求出第三阶段持续时间tf2。
03
3.小结
(1) 本文结合驱动电路、器件模型和测试工况三方面信息,对器件关断过程进行了详细分析计算。梳理了栅极电阻、电容和电感对关断过程的影响。
(2) 在实际应用中,已知栅极参数,可以计算关断各阶段的时间、电压尖峰和电压电流变化率等;已知开关时间、电压尖峰和电压电流变化率等边界条件,可以给出合理的栅极参数取值范围。
(3) 在应用ME400D进行器件动态参数测试时,输入边界条件,可以迅速判断出栅极参数取值的大致范围,并进行自动测试,大大提高测试效率。
*文中提及的ME400D是Firstack全新升级的SiC器件动态特性测试设备,将于2024年发布,敬请期待!
[1]肖先勇,郑子萱.“双碳”目标下新能源为主体的新型电力系统:贡献、关键技术与挑战[J].工程科学与技术,2022,54(01)10.15961/j.jsuese.202100656.
[2]全球能源互联网发展合作组织.中国2060年前碳中和研究报告[R]. 北京:全球能源互联网发展合作组织,2021.
[3]Abhijit D. Pathak. IXYSmosfet_driver_theory_and_applications, IXYS Corporation, 2001.
[4]JEDEC JEP192. Guidelines for Gate Charge (QG) Test Method, 2022.
[5]Fuji Electric. 2MBI600XNG120-50 Datasheet, 2018.
[6]Dong Z, Wu X, Xu H, et al. Accurate analytical switching on loss model of SiC MOSFET considering dynamic transfer characteristic and Qgd[J]. IEEE Transactions on Power Electronics, 2020, 35(11): 12264-12273.
[7]Wang X, Zhao Z, Li K, et al. Analytical methodology for loss calculation of SiC MOSFETs[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 7(1) ; 71-83.
[8]Infineon. FF600R12ME4 Datasheet, 2013.
[9]Wang, Ning, and Jianzhong Zhang. Nonlinear capacitance model of SiC MOSFET considering envelope of switching trajectory[J]. IEEE Transactions on Power Electronics 37. 7 (2022): 7977-7988.
审核编辑:黄飞
-
SiC MOSFET 开关模块RC缓冲吸收电路的参数优化设计2025-04-23 1652
-
Si IGBT和SiC MOSFET混合器件特性解析2025-01-21 2559
-
为SiC mosfet选择栅极驱动IC时的关键参数2023-06-16 1389
-
如何使用电流源极驱动器BM60059FV-C驱动SiC MOSFET和IGBT?2023-02-21 10066
-
SiC-MOSFET器件结构和特征2023-02-07 1437
-
SiC MOSFET:经济高效且可靠的高功率解决方案2019-07-30 4139
-
SiC MOSFET SCT3030KL解决方案2019-07-09 2378
-
SiC功率器件SiC-MOSFET的特点2019-05-07 5552
-
SiC-MOSFET有什么优点2019-04-09 4527
-
搭载SiC-MOSFET和SiC-SBD的功率模块2019-03-12 3310
-
Si-MOSFET与IGBT的区别2018-12-03 3643
-
SiC功率模块的栅极驱动其12018-11-30 3168
-
汽车类双通道SiC MOSFET栅极驱动器包括BOM及层图2018-10-16 2811
-
基于虚拟仪器的IGBT电气参数自动测试系统_姚丹2017-01-08 835
全部0条评论

快来发表一下你的评论吧 !

