Verilog表达式的位宽确定规则

一般规则

很多时候，Verilog中表达式的位宽都是被隐式确定的，即使你自己设计了位宽，它也是根据规则先确定位宽后，再扩展到你的设计位宽，这常常会导致结果产生意想不到的错误。比如：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a,b;
reg [1:0] c1,c2;

initial begin
    a = 4'b0111;
    b = 4'b1111;
 c1 = a & b;
 c2 = a && b;
end

endmodule

 

结果是这样的：

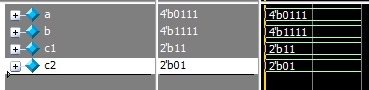
a & b的结果本来应该是4‘b0111 ，但是c1只有2位，所以高位被截断，导致c1为2’b11；而a && b 的结果本来是1位的1’b1，但是c2有2位，所以会在高位补0，导致c2为2’b01。

类似的情况还有很多，为了减少设计出错的可能性，有必要探究一下表达式的位宽确定规则。

Verilog语法规定了如下的确定表达式位宽的规则：

表达式的位宽由表达式中的操作数（operands）或表达式所处的上下文（context）决定。

自决定表达式（self-determined expression）就是表达式中所有操作数的位宽完全由自己决定。

上下文决定表达式（context-determined expression）就是表达式中所有操作数的位宽由整个表达式上下文环境中最大的位宽决定。

自决定表达式

这一类表达式的位宽都是根据表达式自身的位宽和运算结果来决定的。具体规则如下：

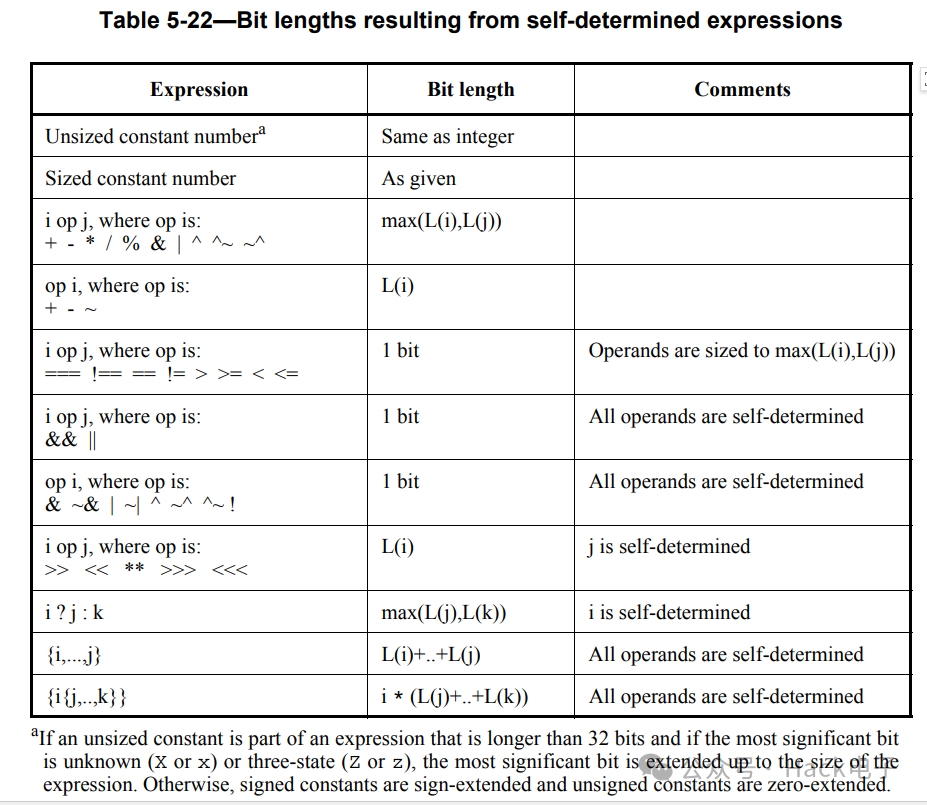
1、无位宽常数

这种情况它的位宽等同于整数integer，在大多数编译器中，integer的默认位宽都为32位。例如modelsim环境下的测试：

 

`timescale 1ns/1ns
module tb_test();

initial begin
    $display("answer = %b", (1)); //以2进制形式打印
end

endmodule

 

打印结果是32位宽的 “1”：

answer = 00000000000000000000000000000001

2、给定位宽常数

没什么好说的，位宽就是给定的这个数，比如 4‘d1的位宽就是4。例如：

 

//以2进制形式打印`timescale 1ns/1ns
module tb_test();

reg [3:0] a;

initial begin
 a = 4'd1;
 $display("answer = %b", a); //以2进制形式打印
end

endmodule

 

打印结果：

answer = 0001

3、运算（1）

i 和 j 做以下运算：+ - * / % & | ^ ^~ ~^ 时，位宽等于 i 和 j 中位宽较大者的位宽。很好理解，这些运算就是常见的 加减乘除取模 与或异或同或 运算。例如4bits数和5bits数相加：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a;
reg [4:0] b;

initial begin
 a = 4'd1;
 b = 5'd1;
 $display("answer = %b", (a + b));
end

endmodule

 

打印结果是5bits：

answer = 00010

4、运算（2）

对 i 做以下运算：+ - ~ 时，位宽等于它本身。也很好理解，就是正负表达和取反，所以位宽肯定不会改变。例如：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a;

initial begin
 a = 4'b1001;
    $display("answer = %b", (~a)); //取反
end

endmodule

 

打印结果仍是4bits：

answer = 0110

5、比较

二个数的比较结果只有 是 和 不是，所以位宽只需要1位，例如：=== !== == != > >= < <=。例如：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a,b;

initial begin
 a = 4'd5;
 b = 4'd3;
 $display("answer = %b", (a > b));
end

endmodule

 

打印结果是1bit：

answer = 1

6、逻辑与、逻辑或

逻辑与&& 和 逻辑或 || 的结果也只有1bit。

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a,b;

initial begin
 a = 4'd5;
 b = 4'd3;
 $display("answer = %b", (a && b));
end

endmodule

 

打印结果是1bit：

answer = 1

7、规约运算（Reduction)

下面这些规约运算的结果只有1位：& ~& | ~| ^ ~^ ^~ !。规约运算就是对数据本身的所有位做同样的对应的运算，例如规约与（该数的所有位相与）：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a,b;

initial begin
 a = 4'b1101; 
 b = &a;  //1 & 1 & 0 & 1
 $display("answer = %b", (b));
end

endmodule

 

打印结果是1bit：

answer = 1

8、移位和乘方

移位和乘方运算（>> << ** >>> <<<）的结果位宽是该数本身位宽。例如移位：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a;

initial begin
 a = 4'b1011; 
 $display("answer = %b", (a >> 1));
end

endmodule 

 

打印结果是4bits：

answer = 0101

乘方运算的结果有可能会溢出，例如：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a,b;

initial begin
 a = 4'd3; 
 b = 4'd3;
 $display("answer = %b", (a**b));
end

endmodule

 

打印结果是4bits：

answer = 1011

3**3的结果原本是27，即1_1011，高位被截断后，成了4bits的1011。

9、条件表达式

条件表达式（i ? j : k）的位宽等于 j 和 k 中的位宽较大者。例如：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a;
reg [5:0] b;
reg    c;

initial begin
 c = 1;
 a = 4'b1011; 
 $display("answer = %b", (c ? a : b) );
end

endmodule 

 

打印结果是6bits：

answer = 001011

尽管c为真，所以该式的结果是a，但是位宽却等于更宽的b，所以结果的高位会补2个0，扩展到6bits。

10、拼接

第一种拼接：{i,…,j}，位宽为二者之和。例如：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a;
reg [5:0] b;

initial begin
 a = 4'b1011; 
 b = 6'b001011; 
 $display("answer = %b", ({a,b}) );
end

endmodule 

 

打印结果是4 + 6 = 10bits：

answer = 1011001011

第二种拼接：{i{j,…,k}}，位宽为二者之和与系数的乘积。例如：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a;
reg [5:0] b;

initial begin
 a = 4'b1011; 
 b = 6'b001011; 
 $display("answer = %b", ({2{a,b}}) );
end

endmodule 

 

打印结果是2*（4 + 6） = 20bits：

answer = 10110010111011001011

上下文决定表达式

上下文决定表达式其实就是各种自决定表达式的集合，所以需要视具体情况而具体分析。看一个例子：

 

`timescale 1ns/1ns
module tb_test();

reg [3:0] a;
reg [5:0] b;
reg [15:0] c;
 
initial begin
 a = 4'hF; //15
 b = 6'hA; //10
 
 $display("a*b=%b", a*b); //10*15
 
 c = {a**b};     //15^10
 $display("a**b=%b", c);
 
 c = a**b;      //15^10
 $display("c=%b", c);
end 

endmodule

 

打印结果：

a*b=010110

a**b=0000000000000001

c=1010110001100001

a*b原本是15×10=150，即1001_0110，但是结果的位宽是a、b中的较大位宽（6bits)，所以被结果截断到 01_0110；

a**b原本是15^10=576,650,390,625，即1000011001000011000010101010110001100001，但是乘法的结果位宽是a的位宽（4bits)，所以结果被截断到 0001；然后和 0 做拼接，相当与位宽没变，所以结果仍是0001，最后赋值给c，c的位宽为16，所以需要在高位补0，最终结果为0000000000000001

第三个和第二个的区别在于没有拼接运算符，a**b的位宽结果取决于上下文环境，即c的位宽。所以在计算时，a和b都会被先拓展到16位，然后再计算结果。