
资料下载

×
基于流行学习的神经网络分类方法
消耗积分:2 |
格式:rar |
大小:1.64 MB |
2018-02-01
维数约简常用于避免高维数据,如图像或文本中的维数灾问题。然而,传统的线性方法,如主成分分析( Principal Component Analysis,PCA)和独立成分分析( Independent Component Analysis,ICA),均假设数据由低维空间线性组成。当数据具有非线性分布时,线性维数约简往往不能有效获得其低维嵌入子空间。
非线性嵌入技术如等距映射(lsometric Mapping,Isomap)算法和局部线性嵌入(Locally Linear Embedding,LLE) 算法等能在数据非线性分布时有效地获得其低维嵌入子空间,但该类算法的不足是:它们常常为所有数据构造一个单独低维子空间,由于不同类别的数据可能会在这个子空间中重叠,使得基于这些非线性嵌入算法的模型分类准确率不高。
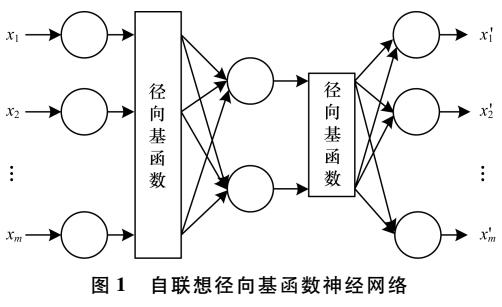
根据现有研究,为每个类别构造一个对应的子空间能有效解决数据重叠问题,从而提升模型的分类准确率。因此,本文提出基于非线性嵌入的自联想神经网络( GSCD Nonlinear Auto-associative Modeling,GNAM)学习样本每一类对应的子空间的方法,并结合集成学习方法.从而实现更有效的分类。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
评论(0)
发评论
- 相关下载
- 相关文章





