AD位数是如何影响信号幅值的？

数据采集设备一个重要的指标就是AD位数，我们都知道AD位数越高越好。但这个“好”到底体现在哪些方面呢？AD位数到底对数据采集有哪些影响呢？

AD位数的实质是指模数转换数据时使用多少位（bit）来表征数据电压幅值大小。这个位（bit）也就是存储二进制数0或1的位数，8位为1个字节（byte）。位数越高，存储小数点后面的位数也就越多，因此，转换后的数据也就越精确，越接近实际值。现今的数据采集设备通常使用24位AD，表示可以用24个0或1来表示数据幅值大小。当然，有1位符号位。

数采设备通过AD进行量化，量化是指现实世界中的时域信号的连续幅值离散成若干个量化量级，实质是幅值转换精度。一个量化量级是指最小的量化电平大小（电平间隔），类似于刻度尺的最小刻度，刻度尺的最小刻度是1mm，1mm之内的读数都是估读出来的，不精确。如果想将最小刻度再提高，这时可以用游标卡尺来测量尺寸，此时，测量的精度更高。AD位数与这个刻度相似，AD位数越高，量化量级（可理解为最小刻度）越小，转换后的数据幅值精度越高，所下图所示。虚线表示相应的量化电平（刻度），所有的转换后的幅值只能位于这些虚线所表示的量化电平之上，其他位置没有任何量化电平。

对于M位AD而言，假设为理想的模数转换器，则其对应的量化量级份数N为：

N=2^MM-1

对于电压满量程为±AV的数采设备而言，其量化量级大小Q为：

Q= 2A/2^MM

通常数采设备的最大满量程是一定的，通常为±10V，因而AD位数越高，量化量级越小，数据转换精度越高。AD位数对应的量化份数和量化量级如下表所示。

从上表可以看出，对于量程相同的情况下，AD位数越高，量化量级越小。假设AD位数为8，则量化电平间隔为78.1mV，模数转化后的幅值电压只能是78.1的倍数，而24位AD转换后的幅值电压则为1.19μV的倍数。这就是为什么AD位数低于16位，包括16位AD的数采设备在AD转换之前需要用放大器，要把AD转换前的信号放大之后再进行量化，以减小量化误差。

下图中考虑将量程为±1.5V用4位和5位AD进行量化，来说明不同AD位数带来的差异。4位AD只能用4位来存储数据，因此，满量程被划分为16份，而5位AD则可以划分为32份。从图中也可以看出，相同的量程高位AD对应的量化电平间隔越小，因此，测量相同的信号，高位AD精度越高。另外，4位AD对应的动态范围为24dB，5位AD对应的动态范围为30dB。关于这一点，将在下面进行说明。

量化误差是模数转换过程中另一个重要的幅值误差源，之前已说过采样频带也会给幅值带来误差。在模数转换过程中，实际模拟量值与量化数字值之间的差异称为量化误差或量化失真。这个误差归咎于取整（只能是量化量级的倍数）或截断造成的，误差大小是随机的，在不同的采样点这个误差大小也不相同。在进行量化时，是将信号的电压幅值按四舍五入的方式量化到最近的量化电平上。在这将通过一个实例数据来说明量化误差是如何产生的。

假设考虑如下图所示的采样，黑色实线表示信号实际大小，采样间隔为时间T，考虑第7个采样点的幅值量化误差。X表示相邻两个量化电平的平均值，从图中可以看出，在采集第7个数据点时，信号的实际幅值大小位于量化电平m6和m77之间，但这个数据量化之后，幅值要么是m66，要么是m7。首先，将该幅值与m6和m77的平均值x6进行比较，发现幅值大于x66，因此，按四舍五入方式量化到最近的量化电平m77上，m77与信号实际值之差即是量化误差。

当AD位数越高时，量化电平间隔会越小，因此，量化误差会越小，转化精度越高。理想的模数转换器，量化误差均匀分布于（−1/2量化量级）~（+1/2量化量级）之间，如理想的24位AD，其量化误差分布于-0.6μV~+0.6μV之间。对于理想的M位AD而言，信号与量化噪声之比(SQNR) （或称为动态范围）可由下式计算

SQNR=20log10(2^MM)=6.02M dB

从上式可以明白，1位AD，对应的动态范围为6.02dB。可以这样理解：由于每一位只能存储0和1，对应的数字大小为1=20和2=21，相差2倍。我们知道，线性2倍，对应6dB。因此，1位AD对应的动态范围为6dB，常见AD位数，对应的SQNR如下表所示。

现在我们已经明白了量化误差，除了用高位AD可减少量化误差之外，还有没有别的方法可以减小量化误差呢？除了用高位AD之外，还有以下两种方法可减小量化误差，提高信噪比。

法1.使用量程合适的传感器

使用量程合适的传感器是为了保证传感器输出的信号大小合适，既不至于过载，又不至于欠载。相对而言，信号幅值越大，信噪比越高，量化误差越小。那到底量程为多大时，使用的传感器是合适的呢？一般而言，测量的信号幅值应在传感器满量程的80%是合适的。如测量位置的振动量级约为40g，则可以用满量程为50g的加速度传感器来测量。如果用量程为500g的传感器来测量，会有什么区别呢？

量程为50g的加速度传感器，对应的灵敏度为100mv/g，则40g对应的电压输出为4V。而当用量程为500g的加速度传感器进行测量时，传感器的灵敏度为10mv/g，则40g对应的电压输出为0.4V。那么，不同量程的传感器测量同一位置的振动时，输出的电压大小是不同的，量程越小，灵敏度越高，输出电压越大，则量化时信噪比越高，量化误差越小。这就是为什么要用合适的传感器来测量的原因。

法2.使用合适的电压量程

当AD位数和传感器已不能更改时，这时可以调节数采设备的电压量程来提高信噪比，减小量化误差。还记得之前的量化量级计算公式Q=2A/2^MM吗？当AD位数确定之后，量化量级的份数也随之确定了，即分母确定了，但是分子为电压量程，可以减小分母，即电压量程，来提高量化量级。比方说，可以把1m划分1000等份，每1份为1mm；如果把0.1m也划分1000等份，则每1份为0.1mm。此时，测量精度会更高，当然，测量的最大距离将从1米变成了0.1m。因此，在测量大信号时用大量程，测量小信号时用小量程。这个量程可调节。

这个量程调节功能也就是所谓的自动量程或手动量程（量程有很多档）。自动量程是根据测量信号的大小，软件自动设置量程；手动量程是测试人员手动修改电压量程。测量大信号时，用大量程，测量小信号时用小量程。设置合适的量程之后，大信号不会因量程不合适而过载，小信号也不会因量程不合适而欠载。

如果对大信号设置的电压量程过小，会导致削波的情况出现，如下图所示。超出量程的部分会被削掉。

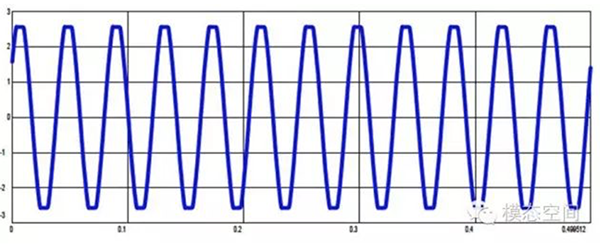
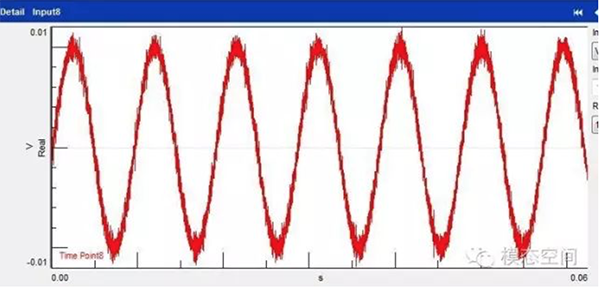
对幅值大小为10mV的信号设置不合适的量程，采集到的信号如下图所示。

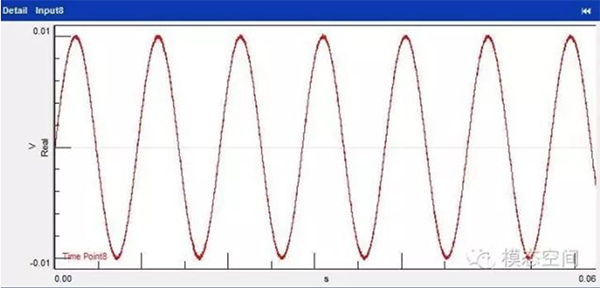
设置合适的量程之后，采集到的信号如下图所示。

对一个单频小信号如果AD和量程设置不合适，可能会如下图所示。从图中可以看出，当用16位AD，不自动量程，即满量程10V进行采集时，采集到的信号如下面顶部图所示，信号为三角波，且台阶明显，这就是量化误差造成的。当用24位AD也不自动量程时，得到的信号如下面中图所示。此时，信号较之前已有明显改善，但量程设置还不合适。当设置合适的量程（0.0625V）之后，单频的小信号信噪比已很高，信号很干净，这正是我们想要的信号。信号从带台阶状的三角波到含有杂波的信号，到最终的干净单频信号，量化误差在逐步减小，信噪比逐步提高，幅值精度越来越高。

到此，我想您已明白AD位数对信号测量的影响了。但是有一点要注意的是，之前我们所说的一直在强调理想的AD，也就是所有的位数都是有效位，不受噪声影响。但现实情况是，不是所有的位数都是有效位。比方说24位AD的动态范围理论上是144dB，但实际的动态范围在110-120dB之间，也就是有效位在18-20位之间。这是因为数采设备都是电子元器件组成的，本身会存在噪声，降低了AD的位数。这个噪声也就是所谓的本底噪声，即使不测量任何信号，设备也有相应的电压输出，这部分电压就是本底噪声。

因此，在信号进行采集时，为了减少误差，我们应尽量使用高位AD，量程合适的传感器和使用合适的电压量程。

本文转自：AD位数是如何影响信号幅值的？