
资料下载

由分立晶体管制成的计算器
描述
我一直对计算机如何在硬件级别上工作感到好奇。当我在读本科时终于了解了操作原理。我的问题终于有了答案。然而,我一直想利用这些知识来设计和构建我自己的逻辑电路,而不是使用门,而是使用分立晶体管本身。这类似于早期计算机的制造方式,当时每个晶体管都是分立的,而集成电路技术还不存在。这些本身就是对体积更大且不可靠的真空管计算机的巨大改进。
我不得不承认,如今使用 SMD 晶体管和中国廉价的 PCB 制造和组装服务,制造晶体管化计算设备要容易得多。我在 7 天内以 5 块多一点的价格制造、组装并运送给我,5 块,非常甜蜜!
让我们来看看最终的结果。
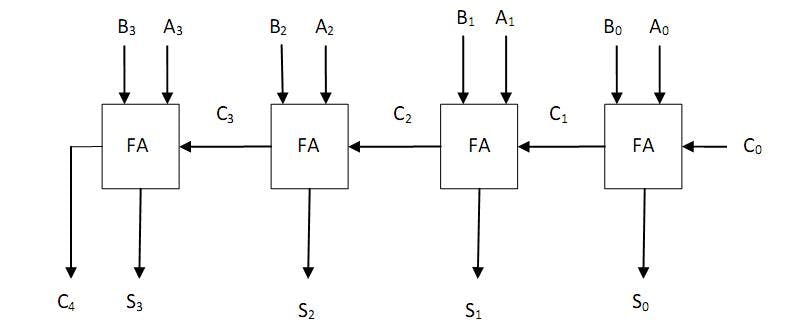
那么它是怎样工作的?如果您仔细查看 PCB,您会看到 4 个独立的电路,每个电路都是一个全二进制加法器。一个完整的二进制加法器只是意味着它可以提供两个 1 位数字A和B的总和,它还考虑到前一个数字的CARRY IN 。作为输出,我们得到了SUM和CARRYOUT。 您可以通过将第一位的进位输出连接到下一位的进位来级联这些全位加法器,并拥有一个可以添加任意大的 N 位数字的电路。在我们的例子中,这个数字是 4。这些电路可以执行加法的方式实际上与我们人类计算两个数字之和的方式非常相似。我们将数字相加并写入总和,如果有进位,我们将其传播到下一个数字。当我们计算下一个数字的总和时,我们会考虑我们之前传播的进位。唯一的区别是我们以十进制数字(0..9)执行计算器,而计算机以二进制执行操作。下图显示了加法器的互连。
现在让我们单独谈谈全加器电路。该电路具有三个输入和四个输出,因此我们可以为此制作一个真值表。我们显示下表。
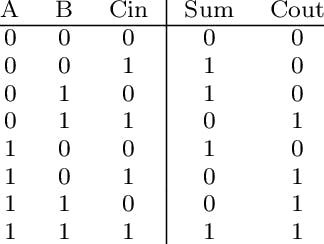
让我快速描述一下这背后的逻辑。二进制数的行为很像十进制数,因此添加相同的逻辑适用。当我们用完要计数的符号时,我们会将其移至下一个数字。对于二进制数,我们只有两个符号 0 和 1。所以当我们将 1 加到 0 时,我们得到 1。但是现在当我们想要再添加一个时,我们没有更多的符号来表示它,所以我们必须携带转发到下一位。如果你考虑这个逻辑,你会发现上面的真值表是有道理的。
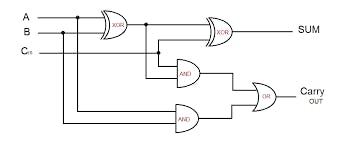
那么我们需要什么样的电路来制作这个呢?好吧,我们可以使用逻辑门。作为一个问题,通过以特定方式组合逻辑门来为任何可能的真值表生成电路。上面真值表的电路是这样的。
现在我们可以使用晶体管来实现这个逻辑电路。这是我的设计。
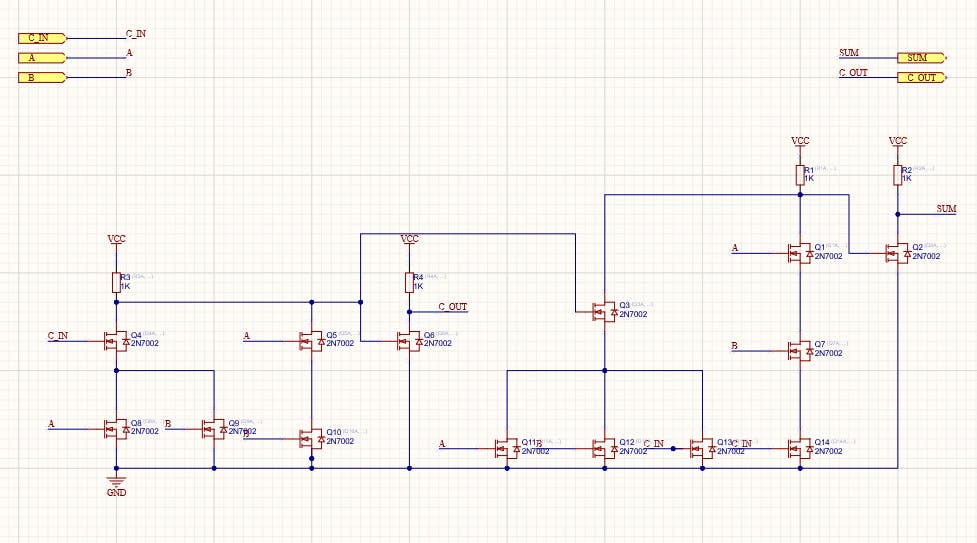
实际上,我们可以应用相同的程序来制作各种逻辑电路,包括减法器、乘法器、多路复用器等。这些是任何 CPU 的基本部分,我们可以扩展这种方法来制作我们自己的基本 CPU。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章








