宽带匹配网络中参量法的数值误差研究

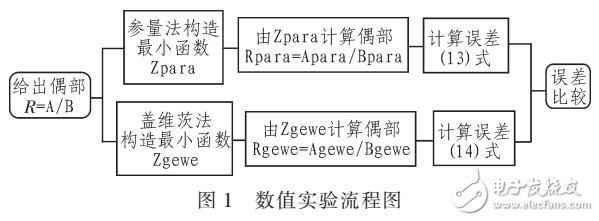
　　在宽带电路以及宽带天线设计中经常需要设计宽带匹配网络，传统解析方法只针对简单负载有效。与解析方法不同，数值方法可以在知道负载实频数据的条件下进行宽带化设计。本文对数值方法中常用的参量法与盖维茨法来构成最小函数的问题进行了理论分析与数值编程，比较了两者在生成最小阻抗函数上的误差大小，且分析了两者产生误差的原因。结果表明，对于阶数比较低的情况，采用参量法和盖维茨法均可行且两者误差几乎相等；但是对于阶数比较高的情况，参量法比盖维茨法的数值误差小几个数量级，这对于设计宽带匹配网络具有很大的指导意义。