
资料下载

如何用Matlab绘制二维图形资料下载
简要
上一篇已经对图形的属性有过介绍,在此基础上来进行二维以及后续三维图形的操作(注:没接触过其他维度的操作,就不折腾相关的内容了),将会更容易理解这些属性的用法,当然,全部的属性使用都来一遍,感觉就不太实际了,大可不必~
简单说下本篇会涉及的内容,常见的plot使用肯定是要有的,然后就是对图形做一些操作,显得更灵活一点,毕竟软件这么强大,不能只局限于画简简单单的图形,此外还有就是一些比较特殊的二维图,比如直方图,柱状图之类的,具体还有啥,慢慢往下看~
~Show Time~
绘制基础
这一段的内容,本来是上一篇想写进去的,不过感觉前后有点不协调,就留到本篇来写了,主要作用就是理解图形的形成机制,和上篇的属性啥的关联不是太大。
要知道,MATLAB是没法真正绘制连续图形的,都是通过”打点“的方式进行绘制,因此要有个离散的概念,比如离散函数y=f(x),然后x的标量数组[x1,x2,x3,...,xn]则对应着y的值[y1,y2,y3,...,yn],然后这两个数组在直角坐标系中以点序列的形式表示,于是就形成了离散的图形,而连续图形的表示则是把离散区间进行细化,逼近连续的形式,在视觉上呈现连续的效果,画图的时候,每两个离散点用线进行连接,则可表示出该函数的连续特性,所以在进行操作图形的时候,要记住点与点之间是对应的,假如x或y缺了点,另一部分就相当于越界了,然后无法对应即绘制失败。
看接下来的两个示例,就可以清楚MATLAB中的连续和离散了
%示例1 离散 x=0:12;%自变量 y=sin(x);%x的对应点 plot(x,y,'r*','markersize',20)%对点进行标记 grid on%开启网格显示
示例1运行结果

%示例2 连续 x=0:0.01:12 y=sin(x);%x的对应点 plot(x,y,'r*','markersize',20)%对点进行标记 grid on%开启网格显示
示例2运行结果

再补充下完整绘图的几个步骤,大致如下:
1)准备数据,二维图形就是准备横坐标和纵坐标的数据,三维图形则需要准备矩形参变量和Z轴数据
2)指定图形窗口和子图位置,可以使用figure命令指定图形窗口,默认是打开Figure1,subplot就可以指定子图的位置,如果像上述那样直接进行了plot,则是默认使用Figure1的窗口
3)绘图,根据数据绘制曲线或曲面图,可对绘制方式进行设置,如:色彩、线型、数据点标记等
4)注释,可以设置坐标轴的坐标范围、刻度等,还能对图形进行注释,如:图名、图例、文字说明等
5)保存图片,可以将绘制的图形保存为.fig后缀的文件,也可转换为其他格式的图形文件
以上几个步骤是相对详细的绘图步骤,一般情况下,只进行了步骤1~3,其余的都是使用的默认设置。
plot
plot是最基本的一个二维图形绘制的函数,输入plot(a,b)就可以画出一个分别以a、b为x轴和y轴的图形,基本的调用格式有以下的几种,即:
plot(x)plot(x,y)plot(x1,y1,x2,y2,..)
plot(x)中的x可以是向量、实数矩阵或者复数矩阵,若x为实向量,则以x的值为纵坐标,各值对应的下标则为横坐标,最后以直线连接各点;若x是复数向量,则实部为横坐标,虚部为纵坐标,然后各点以直线进行顺序连接;若x是个实数矩阵,则按列绘制每列元素值相对其下标的连线图,且同时绘制多条,条数即矩阵列数;若x是个复数矩阵,则分别以x实部矩阵和虚部矩阵的对应元素为横纵坐标绘制多条连线图。
plot(x,y)就要直观一些了,x和y是同维度的向量,以x、y分别为横纵坐标,将相对应的元素值进行连线;若x是个向量,而y是个与x等维度的矩阵,那么绘制出多条曲线,线条数即y矩阵的另一个维数(非与x的相同维数),如果x和y都是矩阵,且等维度,则以x、y对应列元素为横纵坐标进行绘制,曲线条数为矩阵行数。
plot(x1,y1,x2,y2,...)就跟plot(x,y)相同了,只是多了元素对,且不同元素对之间不存在约束关系,相对比较独立,只是在同一个figure里进行显示。
接下来用plot进行一些使用操作:
绘制多条曲线 clear all close all clc x=0:0.05:5;%x坐标 y1=0.1*x-0.5;%y1坐标 y2=sin(x.^2);%y2坐标 figure plot(x,y1,x,y2)
结果

%2 变量为矩阵时的图例
clear all close all clc x=0:pi/180:2*pi; y1=sin(x); y2=sin(2*x); y3=sin(3*x); X=[x;x;x]'; Y=[y1;y2;y3]'; plot(X,Y,x,cos(x))
结果

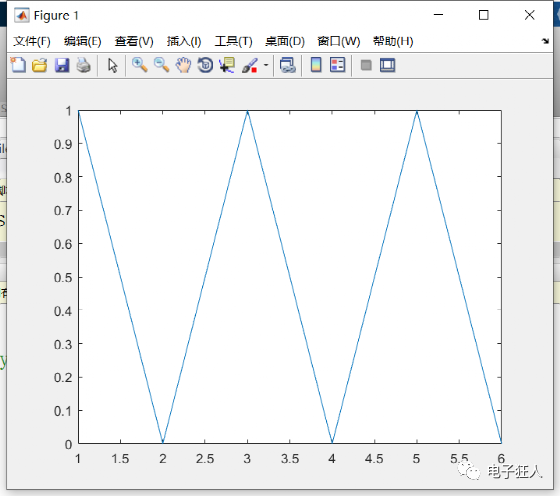
%3 含y坐标变量的锯齿波 y=[1 0 1 0 1 0]; plot(y)
结果
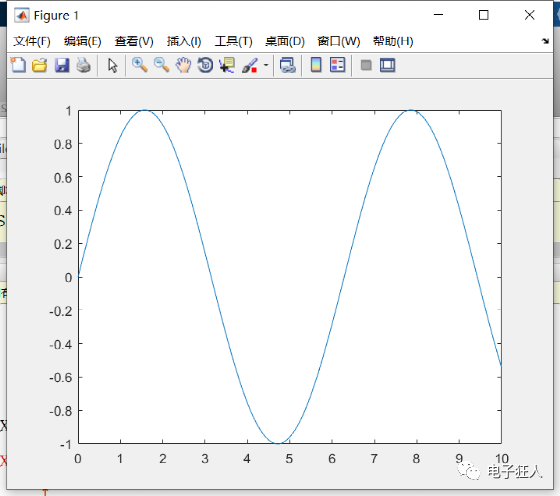
%4 正弦波 x=0:0.01:10; y=sin(x); plot(x,y)
结果
%5 绘制双矩阵 x=[1 2 3;4 5 6;7 8 9]; y=[3 2 1;6 5 4;9 8 7]; plot(x,y)
结果

文字标注
一般情况下,我们都会给绘制的图形添加文字标注,主要的标注方式有以下几种,其中所述的属性名和属性值就是上篇的绘图基础所涉及的。
(1) 添加图形标题
使用title命令,使用格式有两种,即:
title('string')%在坐标系顶部添加一个文本串即string作为该图形标题 title('text','属性名','属性值','...')%设置标题名的属性,可以是字体大小、字体名以及字体的粗细等
(2)添加坐标轴标注
使用xlabel、ylabel、zlabel,分别对应x、y、z三个轴,使用方法相同,以xlabel为例表述
xlabel('text')%给当前坐标系中的x轴添加文本标注,即此处的“text” xlabel('text','属性名','属性值','...')%设置坐标轴标注文本的属性,可以是字体大小、字体名以及字体的粗细等
(3)图例
使用legend函数进行设置
legend(str1,str2,str3,...)%在当前图中添加多个图例 legend off %关闭当前坐标图上的图例
(4)文本注释
使用text函数在二维和三维图形的指定位置进行文本注释,gtext函数可设置文本注释可拖动,即通过鼠标移动,单击后来确定标注的位置。
text(x,y,'string');%在二维图的(x,y)的位置标注'string' text(x,y,z,'string');%在三维图的(x,y,z)的位置标注'string' gtext('string')%使用鼠标移动从而确定‘string’的标注位置
示例
程序
x=0:pi/50:2*pi; y1=sin(x); y2=cos(x); figure(1);plot(x,y1,'k-*',x,y2,'b-o');%创建图形窗口,并对显示图形 grid on;%打开栅格 legend('sin(\alpha)','cos(\alpha)');%添加2个图例 text(pi,0,'\leftarrow sin(\alpha)');%(pi,0)的位置添加文本注释 gtext('cos(\alpha)\rightarrow');%cos曲线的文本注释,由使用者通过鼠标移动,单击后确定放置位置 title('sin(\alpha) & cos(\alpha)');%添加标题 xlabel('\alpha');%添加x轴标注 ylabel('value')%添加y轴标注
结果

线型、点型和颜色
这三个词对应的就是使用plot函数进行绘制图形时,对图形的控制,你想要怎样线型或者点型的图,颜色又想要怎样的,这些都很适用,为了方便理解和使用,将这些标识符以表格形式进行展示:
|
颜色标识符 |
符号标识符 |
线型标识符 |
|||
|
r |
红 |
. |
点 |
- |
实线 |
|
g |
绿 |
o |
圆圈 |
: |
点线 |
|
b |
蓝 |
x |
x号 |
-. |
点划线 |
|
c |
青 |
+ |
+号 |
-- |
虚线 |
|
m |
品红 |
* |
星号 |
|
|
|
y |
黄 |
s |
平方号 |
|
|
|
k |
黑 |
d |
钻石 |
|
|
|
|
|
v |
三角符号(向下) |
|
|
|
|
|
^ |
三角符号(向上) |
|
|
|
|
|
<< spa> |
三角符号(向左) |
|
|
|
|
|
> |
三角符号(向右) |
|
|
|
|
|
p |
五角星 |
|
|
|
|
|
h |
六角星 |
|
|
之前用plot的时候也已经用过很多次了,这边再简单用几个标识展示下
x=0:0.1:10; y1=sin(x); y2=cos(x); plot(x,y1,'d-',x,y2,'hc--')
结果

坐标轴设置
在绘图的时候,如果没有对坐标轴进行设置,MATLAB将使用默认模式,即直角坐标系,并自动标记刻度,如果有特定的需要,则可以对坐标轴进行设置,可以设置坐标比例、坐标边界范围以及坐标轴的形式。
坐标轴的控制指令是axis以及axis+控制指令,下方列出一些常用命令及其含义;
|
命令 |
含义 |
|
axis([xmin,xmax,ymin,ymax]) |
设定坐标范围,需满足xmin |
|
axis auto |
使用默认设置 |
|
axis manual |
使当前坐标范围不变,之后的图形都在当前坐标范围显示 |
|
axis fill |
在manual方式下起作用,使坐标充满整个绘图区域 |
|
axis vis3d |
保持高宽不变,三维旋转时,避免图形的大小变化 |
|
axis ij |
矩阵式坐标,原点在左上方 |
|
axis xy |
普通直角坐标系,原点在左下方 |
|
axis equal |
横、纵坐标采用等长刻度 |
|
axis on |
使用轴背景 |
|
axis off |
取消轴背景 |
|
axis tight |
把数据范围直接设置为坐标范围 |
|
axis square |
使得坐标系为方形 |
|
axis normal |
默认矩形坐标系 |
|
axis image |
横纵轴采用等长的刻度,且坐标框紧贴数据范围 |
示例
%1 使用默认设置的坐标轴 z=0:0.1:2*pi; x=sin(z); y=cos(z); plot(x,y); axis auto
结果1

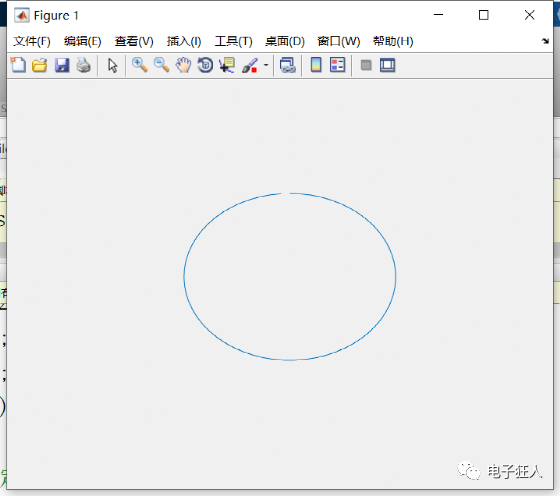
%2 使用坐标轴为方形 z=0:0.1:2*pi; x=sin(z); y=cos(z); plot(x,y); axis square
结果2

%3 设定坐标轴范围 z=0:0.1:2*pi; x=sin(z); y=cos(z); plot(x,y); axis([-2 2 -2 2])
结果3

%4 设定坐标轴范围且关闭背景 z=0:0.1:2*pi; x=sin(z); y=cos(z); plot(x,y); axis([-2 2 -2 2]); axis off
结果4
图形叠加绘制
在很多时候,我们会在一张已有曲线的图形上再绘制一条或多条曲线,从而对各种曲线的关系进行对比分析等,因此在MATLAB中提供了hold命令实现该种功能;
hold on%使得当前轴以及图形保持而不被刷新掉,然后在此图中绘制新图 hold off%使得当前轴以及图形具备刷新的性质,即新图替换旧图 hold %直接相当于on和off的双向切换
示例
%绘制离散信号通过零阶保持器后的波形 t=2*pi*(0:20)/20; y=cos(t).*exp(-0.4*t); stem(t,y,'g'); hold on; stairs(t,y,'r'); hold off;
结果

子图绘制
子图很常见,就是在一个窗口里布置多个独立的图形,使用subplot函数
subplot(m,n,k)%图形窗口中将有(m x n)幅子图,k是当前子图的编号,编号从左到右,从上到下增加 subplot('position',[left bottom width height])%在指定位置开辟一定宽高的子图,并设为当前图,其中[left bottom width height]为设置值,取值范围[0~1],左下角为(0,0)坐标位置
注:由于子图是独立的,因此所有的绘图指令都可以在子图中使用;若使用subplot后,想要重新在整个窗口绘图,则可使用“clf”命令清除已绘图形再进行绘制,当然直接用close,然后重新创建也可。
示例
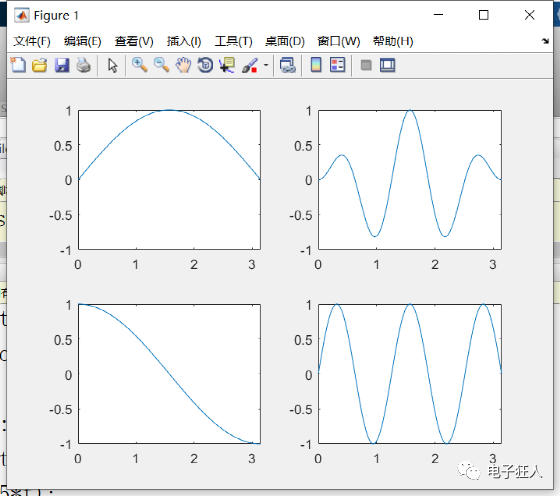
%例1 t=(pi*(0:1000)/1000)'; y11=sin(t); y22=sin(5*t); y12=y11.*y22; y21=cos(t); subplot(221);plot(t,y11);axis([0,pi,-1,1]); subplot(222);plot(t,y12);axis([0,pi,-1,1]); subplot(223);plot(t,y21);axis([0,pi,-1,1]); subplot(224);plot(t,y22);axis([0,pi,-1,1]);
结果1
%例2 t=(pi*(0:1000)/1000)'; y11=sin(t); y22=sin(5*t); y12=y11.*y22; y21=cos(t); subplot('position',[0.1 0.5 0.35 0.35]);plot(t,y11);axis([0,pi,-1,1]); subplot('position',[0.5 0.5 0.35 0.35]);plot(t,y12);axis([0,pi,-1,1]); subplot('position',[0.1 0.1 0.35 0.35]);plot(t,y21);axis([0,pi,-1,1]); subplot('position',[0.5 0.1 0.35 0.35]);plot(t,y22);axis([0,pi,-1,1]);
结果2

未完待续
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章






