
资料下载

ApproxFFT:Arduino最快的FFT函数
描述
FFT或快速傅里叶变换是信号处理中最重要的工具之一。这可用于以良好的速度检测频率。然而,这是一个计算密集型过程,需要大量的处理能力和内存,尤其是在 Arduino 上。这使得它很难用于每秒需要多个 FFT 结果的实时应用程序。
在本教程中,介绍了在 Arduino 上执行 FFT 的最快程序。我将其命名为 ApproxFFT,因为在多个阶段采取了如此多的近似值。然而,几乎没有妥协的不准确性,我能够达到大约 3 倍的速度。
如果您只想知道如何使用它,请直接转到 5。
整个项目也在半小时长的解释视频中进行了解释。您可以选择阅读或阅读本教程。
我之前为同一个应用程序准备了两个代码,可以在此处访问:EasyFFT :此代码为 FFT 提供准确的输出,但是,它相对较慢并且消耗大量内存。建议先阅读本教程以了解 FFT 的背景知识到本教程。
QuickFFT :此代码提供了非常快速的输出。然而,幅度相距甚远,不能用于大多数应用。它还给出了可能误导结果的多个峰。
1:ApproxFFT函数的需要
如果您参考附图,很明显 QuickFFT 与传统方法相比具有一些显着优势(使用 EasyFFT 的内置正弦/余弦函数计算速度)。它几乎快 4 倍,但缺乏准确性。从第二张图中可以看出,幅度相差甚远。这背后的主要原因是我们使用了由多个频率(谐波)组成的方波(近似正弦波!!!)。结果中存在多个波,这使得各种应用程序变得困难。
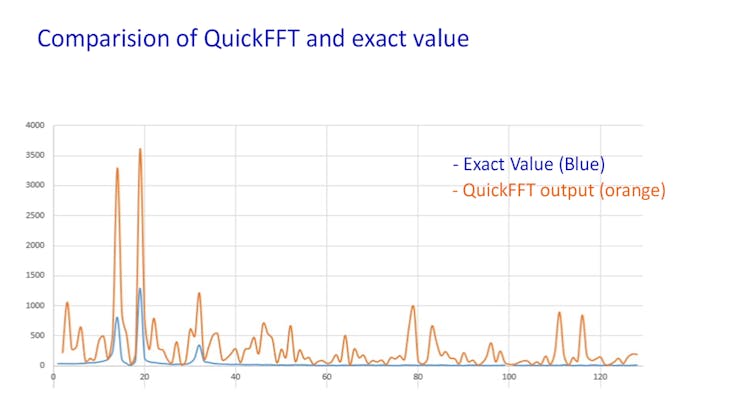
1 / 2 •比较
在这里,我们假设正弦/余弦波为方波。如果我们对这些波进行更好的近似,我们可以接近精确的输出。在此代码中,为这些波考虑了更好的近似值。我们也有一些规定来控制这些波的准确性。通过调整此设置,我们还可以使用各种精度/速度关系。
2:快速正弦和余弦函数
如果您参考之前的 EasyFFT 函数,我们有两个选项可用。其中之一是准确的利用内置的正弦/余弦函数,这些函数准确但速度慢。如果我们使用另一种使用查找表的方法,速度会略有提高,损失不准确。
1 / 2
这里使用完全不同的方法来计算这个值,比传统方法快 10-12 倍。这些函数集中使用仅移位操作进行乘法和(近似)除法。这些操作比正常的除法或乘法快得多。但是,这些可能会导致我们需要以某种方式处理的精度损失。
下面两行是使 EasyFFT 和 QuickFFT 之间的速度差异的行。通常首先我们必须计算给定值的正弦/余弦。一旦该值可用,就需要乘以另一个浮点值。这两个过程都很慢并且需要太多时间。
tr=c*out_r[i10+n1]-s*out_im[i10+n1];
ti=s*out_r[i10+n1]+c*out_im[i10+n1]; // c is cosine and s is sine of some value
在这里,我们使用了类似于二进制支撑算法的东西。它将直接给出 A*sin(θ) 的近似输出,我们不需要进行乘法运算。在第一个图中,显示了 ArcsinX 与 X 的图。一个类似的情节是一个商店作为 Arduino 中的桌子。其中角度从 0-1024 映射,相当于 0-360 度。反正弦值也被视为 128 的倍数。
这就是计算流程的工作方式:这里我们忽略负值,只考虑 0-90。(即 500*sin 50(度数))
1. 对于任何值(即 500),正弦倍数可以是 0(对于 0 度)到该值(对于 90 度)(即 0-500)。我们将检查中点的角度值。我们将输入值的一半 (500) 并检查 0.5 的角度。基于此,我们可以检查输出将是 0-mid point 或 midpoint-max(在我们的情况下,0.5 的角度将是 30 度,低于 50,因此我们可以得出结论,输出将在 250-500 之间)。此时,我们已将可能范围的大小减半。(以前的 0-500 到 250-500 )
2.新定义的范围我们将再次做类似的步骤重复。在我们的示例中,中点为 375,我们将检查角度为 75,即 48 度。所以我们的答案将在 375 到 500 之间。
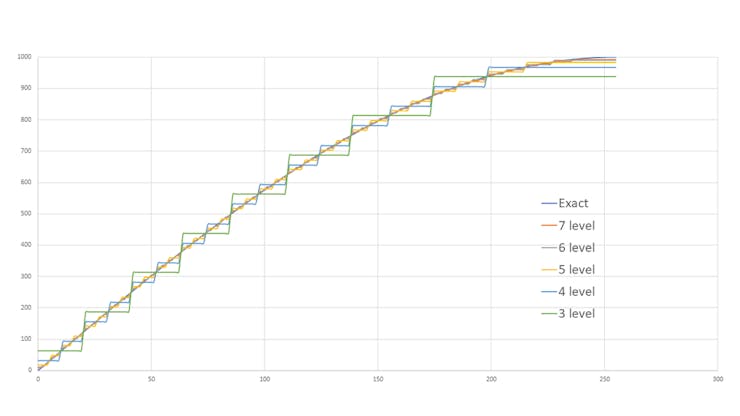
类似的步骤需要重复多次才能准确输出。如第二张图片(图表)所示。我们进入的级别越多,输出将越接近精确值。
在这里,我们可以只通过位移来执行所有操作,并且我们还消除了浮点乘法。
3:平方和的快速根(FastRSS)
这个函数对 RSS 值做了一些近似。它对整体速度的影响不是很显着。但是,它节省了几毫秒的时间。
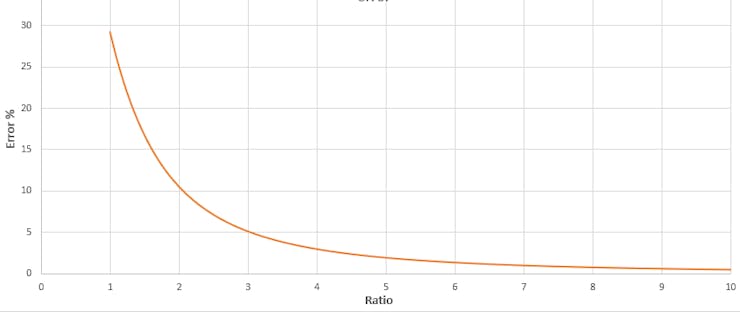
如果我们假设平方和输出与较大值相同,则所附图表显示了误差值。与此假设相关的误差随着比率的增加而减小。在此代码中,如果比率超过它只是假设一个较大的值作为输出以节省时间。如果该比率低于该比率,则基于该值设置一些预定义的缩放比例,该比例通过执行一些重复来应用。所有这些值都存储为 RSSdata。
4:整体计算流程:
整体计算流程如下。
1.输入数据缩放到+512到-512:这一步对于保持数据的精度很重要。由于我们使用的是位移操作,所以在奇数的情况下会有精度损失。数字越大,损失越小。
2. 位逆序生成,
3. 输入数据按照生成的位倒序排列。
4.进行频率变换。需要时使用快速正弦和余弦。每次循环后,所有整数的值检查幅度是否高于 15000,实数和虚数数组均除以 2。
无论在何处执行缩放,都会记录缩放值。
5. 使用 FastRSS 函数计算平方和的根。
6. 检测最大值并作为输出返回。
5:应用
1.查找数据需要声明为全局变量。我们只需将以下数据粘贴到代码顶部即可。
//---------------------------------lookup data------------------------------------//
byte isin_data[128]= {0, 1, 3, 4, 5, 6, 8, 9, 10, 11, 13, 14, 15, 17, 18, 19, 20, 22, 23, 24, 26, 27, 28, 29, 31, 32, 33, 35, 36, 37, 39, 40, 41, 42, 44, 45, 46, 48, 49, 50, 52, 53, 54, 56, 57, 59, 60, 61, 63, 64, 65, 67, 68, 70, 71, 72, 74, 75, 77, 78, 80, 81, 82, 84, 85, 87, 88, 90, 91, 93, 94, 96, 97, 99, 100, 102, 104, 105, 107, 108, 110, 112, 113, 115, 117, 118, 120, 122, 124, 125, 127, 129, 131, 133, 134, 136, 138, 140, 142, 144, 146, 148, 150, 152, 155, 157, 159, 161, 164, 166, 169, 171, 174, 176, 179, 182, 185, 188, 191, 195, 198, 202, 206, 210, 215, 221, 227, 236}; unsigned int Pow2[14]={1,2,4,8,16,32,64,128,256,512,1024,2048,4096}; byte RSSdata[20]={7,6,6,5,5,5,4,4,4,4,3,3,3,3,3,3,3,2,2,2}; //---------------------------------------------------------------------------------//
2、ApproxFFT、fast_sine、fast_cosine、fastRSS函数需要贴在代码末尾。
3、使用功能:
float f=Approx_FFT(data,sample,sampling_rate);
该函数默认返回最大振幅的频率值。这与 EasyFFT 和 QuickFFT 函数完全相同。
首先是我们需要执行 FFT 的数组,
第二个是样本数:理想情况下,它应该是 2^n,可以是 2、4、8、16、32、64、128,..这里的最大样本数受可用内存的限制
第三个输入是采样率。
4.精度设置:
该值可以设置为 1 到 7。数字越高,精度越高。这里提高精度将提高我们近似正弦波的拟合度。默认情况下,精度值设置为 5。在大多数情况下,此值效果很好。所有结果和速度声明均基于此值。可以通过更改此值来调整速度和准确性。
int fast_sine(int Amp, int th)
{ int temp3,m1,m2; byte temp1,temp2, test,quad,accuracy; accuracy=5; // set it value from 1 to 7, where 7 being most accurate but slowest // accuracy value of 5 recommended for typical applicaiton while(th>1024){th=th-1024;} // here 1024 = 2*pi or 360 deg while(th<0){th=th+1024;} . . .
5. 可以修改此代码以显示(和使用)各种频率的原始输出或幅度。输出将是 2^n 的倍数。由于整数最多只能容纳 +-32000 个值,因此输出表示为倍数。
六,结论
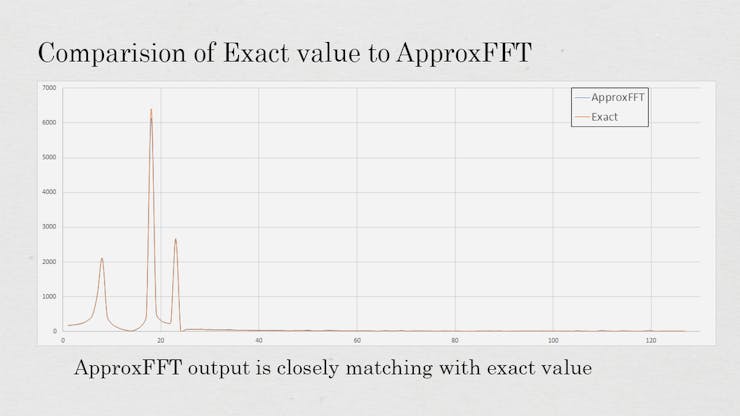
1 / 2
上图中显示的所有测试都是在 Arduino mega 上完成的,精度为 5。以下是测试中的一些重要观察结果:
速度比传统FFT快3倍以上,
内存消耗低(几乎一半),
输出与精确值相当(低误差),
希望这段代码对项目有用。如有任何疑问或反馈,请通过评论或电子邮件告诉我。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章






