
资料下载

QuickFFT:Arduino的高速(低精度)FFT
描述
典型的 Arduino 具有有限的 RAM 和处理能力,而 FFT 是一个计算密集型过程。对于许多实时应用,唯一的要求是获得最大振幅的频率或检测频率峰值。
在我的一个教程中,我准备了一个 FFT 代码,可以在这里找到:EasyFFT
此代码能够在 Arduino nano 上执行多达 128 个样本的 FFT。由于 Arduino 的内存有限,不可能有比这更高的样本数。我稍微修改了函数以提高速度并减少内存消耗。这种修改允许 Arduino 以五倍的速度执行 FFT,并消耗几乎一半的内存。本教程不涉及 FFT 的工作,可以在EasyFFT中找到它的参考资料。
在职的
修改了典型的 FFT 函数以提高速度,但精度较低。如图所示,测试信号需要乘以正弦或余弦波形。这些值可以在 0 到 1 之间,因此必须进行浮点乘法。在 Arduino 中,浮点乘法比整数运算慢。
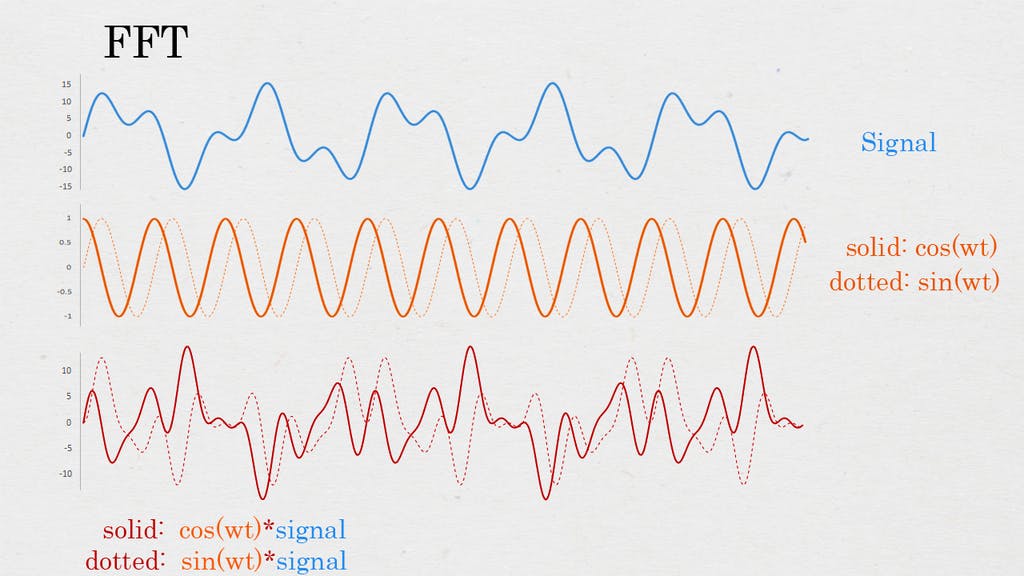
在此功能中,正弦/余弦波被方波代替。因为我们必须将测试信号与可能具有值 0、1 或 -1 的方波相乘。因此,我们可以将浮点乘法替换为简单的整数加法或减法。对于 Arduino 整数加法或减法大约快 5 倍。这使得求解速度提高了大约 5 倍。
由于这种修改,现在频率 bin 值可以存储为整数(以前是浮点数),并且我们获得了另一个降低内存消耗的优势。在 Arduino Nano 中,int 消耗 2 个字节的内存,而 float 消耗 4 个字节的内存。由于新代码的这一优势,我们能够对近 256 个样本(之前为 128 个样本)执行 FFT。
在 Normal FFT 中,我们需要存储正弦值以加快求解速度。在新功能中,由于我们不再需要正弦/余弦值,我们可以消除它并节省一些内存。
执行:
实现这个功能很简单。我们可以简单地复制代码中的函数。可以使用以下命令执行此功能:
float f= Q_FFT(data,256,100);In function Q_FFT,
数据:该术语是具有信号值的数组,推荐的样本大小为 2、4、8、32、64、128、256、512、... 等。如果样本大小不属于这些值,它将被剪裁到最近的值的下侧。例如,如果样本大小为 75,则将对 64 个样本执行 FFT。最大样本数量受 Arduino 上可用 RAM 的限制。
第二项指定数组中的样本数,最后一项是以 Hz 为单位的采样频率。
第 2 步:代码
本节说明在EasyFFT代码中所做的修改,在代码中进行修改时需要牢记,
1. 如前所述,这里使用整数进行 FFT。Arduino 中的 Int 是一个 16 位数字,可以包含从 -32768 到 32768 的值。只要这个 int 的值超过这个范围,就会导致问题。在水平计算后消除这个问题。如果任何值超过 15000 个完整的数组将除以 100。这将防止 int 溢出。
2、幅值计算:计算幅值时,需要对实部和虚部取平方,求和的平方根。平方和函数的平方根是耗时的。为了使这个过程更快,这段代码将简单地做一些实部和虚部的量级。这肯定不太准确,并且在某些情况下可能导致错误的结论。您可以选择返回 Normal 方法进行幅度计算,但这需要更多时间,并且您还需要做一些安排来存储这些数字。
3. 本代码没有多峰检测模块。它将简单地选择具有最大幅度的值(不包括第一个数字,即直流偏移)。如果您需要多个峰,您可以参考EasyFFT代码并在此处进行所需的修改。在这种情况下,一些数组/变量也需要声明为全局变量。
4. 该函数包含以下行:
unsigned int Pow2[13]={1,2,4,8,16,32,64,128,256,512,1024,2048};
将上述变量声明为全局变量(将其粘贴在代码开头)将在每次执行时节省 1 毫秒的时间。
5. 与 EasyFFT 函数不同,其中前 5 个峰存储在预定义的数组中。此函数将返回一个浮点值。该值表示以赫兹为单位的具有最大幅度的频率。所以代码的表示看起来像这样。
float f= Q_FFT(data,256,100);
6. 峰值检测:一旦找到具有最大幅度的频率,此功能将使用其前后的频率幅度来计算准确的结果。此计算中使用的幅度也是模数的总和(不是平方和的平方根)
如果 Fn 是具有最大幅度的频率,则可以通过以下公式计算频率。
实际 F= ( An- 1 *Fn-1 + An-1 *Fn-1 + An-1 *Fn-1 ) / (An-1+An+An+1)
其中 An 是频率 n 的幅度,Fn-1 是频率值。
第 3 步:结果:
上图与EasyFFT的比较显示了求解时间。它的速度与比较显示。

显示了具有 3 个不同频率的正弦波的样本数据。QuickFFT 的结果与 Scilab 输出进行比较。正如我们在图像中看到的,最大振幅的 3 个峰值与 Scilab 输出相匹配。但是,输出包含大量噪声,这可能会误导某些应用程序。因此,建议在申请您的应用程序之前正确检查代码。
我希望您发现此代码对您的项目有用。如有任何疑问或建议,请发表评论。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章






