
资料下载

圆锥滚子修形对接触副应力分布的影响
滚动轴承作为一种重要的基础机械部件,在各种旋转机械中得到广泛的应用,它们的运行状态往往直接影响整个机械系统的性能。圆锥滚子与滚道的接触属于典型的有限长线接触问题,在滚子端部会出现明显的应力集中现象,即“边缘效应”,是导致滚动轴承产生早期疲劳剥落的主要原因。为了消除或减小这种应力集中现象,提高轴承的承载能力、使用性能和寿命,人们提出了对滚子进行修形设计。
在圆锥滚子轴承中,滚子和滚道的接触问题一般采用数值计算方法进行求解。一种方法是基于有限元法,它的特点是可以获得内部的应力场,但由于是三维应力集中问题,解题规模比较大;另一种方法是将表面接触应力分解为作用于相应节点上的集中力,在二维区域内直接对弹性接触问题的基本方程进行离散处理,计算量相对较小,常见的有影响系数法、共轭梯度法等;再者,Hoeprich 在计算修形滚子与滚道的接触应力分布时采用了一种简化的一维计算方法,即改进的切片法;同时,国内的罗继伟对此计算方法也进行了深入地研究。该方法基于对积分方程的数值求解,对滚子横向的接触应力按Hertz分布迸行假设,在圆柱滚子轴承接触分析中,获得了满意的结果。以上方法中,影响系数法的可靠性及数值稳定性较好,虽然其计算时间随网格单元数的增加而延长,但仍被广泛地使用。
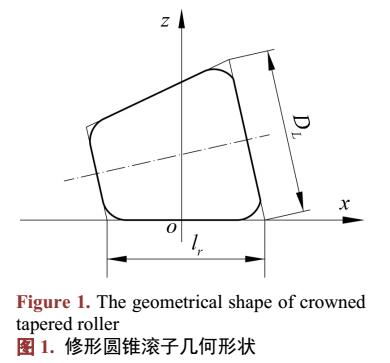
本文使用影响系数法对直母线、圆弧修形和对数修形三种滚子修形情况下的滚子一滚道接触副的接触应力进行分析,研究不同工况下滚子修形对应力分布的影响,为滚动轴承中滚子修形提供理论基础。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章






