
资料下载

研究Chua电路中的非线性谐振
描述
什么是非线性共振?
共振被定义为一种物理现象,其中动态系统的响应由于施加的周期性力而达到最大幅度。然而,什么是动力系统和周期力?在深入实验之前,将在以下几行中提供简要说明,以展示概念上的直觉。
**** 请注意,具有物理或数学背景的读者可以跳过介绍的第一部分,直接进入项目目标和实验。
1.动力系统
名词用于表示日常物品。例如,如果人们观察到在高速公路上行驶的由四个轮子支撑的组装金属片,就会想到汽车这个词。定性描述让我们无需花费太多脑力就可以交流和描述日常物品。尽管非常有用,但定性表示并没有考虑到我们周围环境的全部复杂性。当需要具体细节时,量化变得必要。分配了一组物理值,如尺寸、温度、质量,以进一步澄清。在大多数情况下,分配给对象的量化值随时间保持不变。然而,特殊类型的对象需要不同形式的量化来表示它们的全部复杂性。具体来说,用作描述的量化值不会随着时间的推移保持不变。例如,一朵花的精确尺寸不能取一个特定的值,因为它在任何时候都在缓慢地进化。它需要一个函数来描述维度如何演变。也就是说,花就是我们所说的动力系统。自然界中存在许多其他例子,从而产生了令人着迷的行为。
动力系统的日常示例:
-摆动摆(势能和动能之间的恒定周期性变化)
-人口增长(由于捕食者/猎物的相互作用和繁殖,人口的持续周期性增加和减少)
-人脑(神经元细胞中化学信号浓度的持续周期性变化)
2.周期力
力量引起变化。它通常被称为能量转移,给定物体改变其自然状态。例如,如果朝给定方向施加很小的力,坐在桌子上精确位置的一杯茶会发生变化。当施加的刺激随时间不恒定时,力就会变成周期性的。例如,每次达到最大高度时推动坐在摆锤上的孩子被认为是周期性的,因为外部动作仅在特定时刻发生。正是这种周期性的外部作用导致系统或对象发生变化,称为周期性力。
周期性力或刺激的日常示例:
-人类感官- 光波与眼睛的光感受器相互作用并允许视觉。声波刺激耳膜,使音乐愉悦。
-季节- 影响生物生态系统的温度等环境条件的周期性变化。
-交流电- 改变电子电路内部动态的周期性输入信号。
现在对动力系统和周期性扰动的原理有了简要的了解,我们不得不怀疑动力系统由于周期性刺激而可能表现出的响应。例如,如果外部推动的幅度不断增加到无穷大,而施加的频率与摆的自然摆动频率完美匹配,那么坐在摆摆上的孩子会发生什么?毫无疑问,大自然能够做出令人震惊的反应!
3.共振
当动态系统的振幅由于施加的周期性力而被驱动到最大值时,就会发生共振。例如,即使在正确的时刻施加了最小的力,摆锤的幅度也会急剧增加。例如,当且仅当孩子在摆锤的势能处于最大值时周期性地施加外部推力时,发现自己坐在摆动的钟摆上,而孩子施加最小的推动力,仍会将摆动幅度增加到最大值。在这种情况下,孩子的外部动作被称为在摆锤上引起共振。
毕竟,我们为什么要关心共振现象呢?
令人惊讶的是,我们的生活在很多方面都依赖于共振:
- 电信- 无线电通信是通过作用在电子电路上的电磁信号的共振作用而发生的。
- 核磁共振- 电磁场对原子核的共振作用可以获取有关各种化学和生物材料的物理信息。
- 塔科马窄桥灾难- 忽视共振的力量可能会导致意外故障。例如,小风扰动导致塔科马窄桥倒塌。请注意,共振是否是灾难的根本原因仍然存在争议。无论如何,塔科马大桥灾难表明,由于小的周期性扰动,通常会表现出令人惊讶的反应性质。
- Chladni 板实验- 声音在具有沙子的振动板上的感应作用,根据振动频率创建美丽的几何图案。该实验使与振动性质相关的几何图案栩栩如生。
- 酒杯因声音的作用而破碎- 该实验展示了声波在酒杯上引起共振并因此导致酒杯破碎的能力。
- 共振在音乐中的重要性——麻省理工学院的 Walter Lewin 博士进行了一次非常足智多谋的讲座,展示了共振在音乐中的作用。
我们如何通过实验观察共振?
在许多可用于研究谐振的方法中,电子电路作为一种有效的实验模型出现,因为可以通过改变组件的电子特性轻松修改电路的动态特性。1983 年,Leon O. Chua提出了表现出混沌行为的最简单的电路配置之一。换句话说,蔡氏电路表现出复杂的非线性行为,并作为一个完美的实验系统出现,可以进一步深入了解非线性共振。
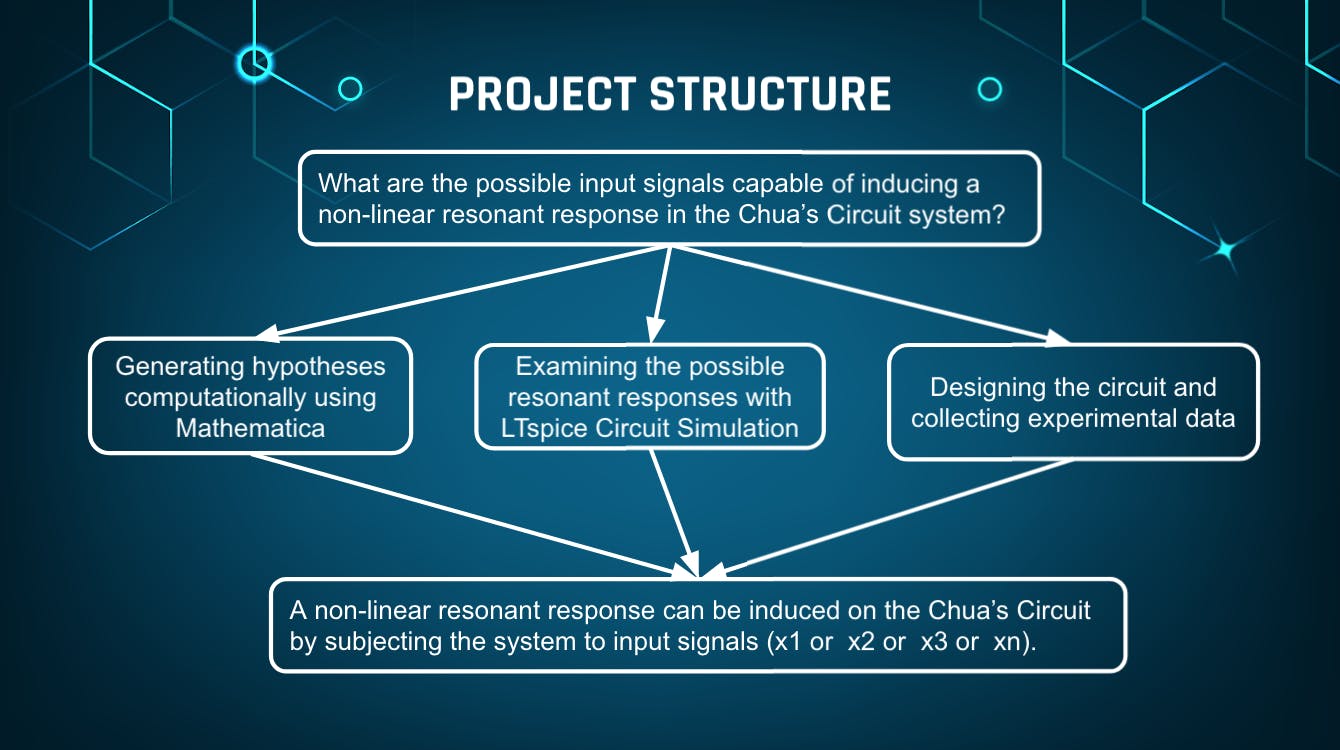
本项目探讨了受各种输入信号影响的 Chua 电路中的非线性谐振。具体而言,能够在蔡氏电路系统中引起最大幅度响应的可能外部信号是什么?答案的路径分为三个部分:
1)首先,从理论上回顾各种共振形式的理论原理。Mathematica软件将被用作允许达到理论直觉的计算环境。
2)在阐明了解释共振现象的理论参数之后,将通过使用LTspice的电路仿真来探索蔡氏电路。
3)最后,将按照 Chua 的设计,通过设计和制造 PCB 板来收集实验测量结果。设计过程将使用Eagle软件进行。电路的生产将依赖JLC PCB作为制造厂。组装完成后,将使用信号发生器使电路承受各种输入信号,并使用示波器测量输出响应。
总体而言,本项目将引导年轻学生或好奇的个人使用蔡氏电路作为实验系统更多地了解共振现象。此外,对于想要探索电子电路中的混乱行为的个人来说,Chua 电路的设计过程可能会变得非常丰富。如果需要有关所遵循的程序和基础理论的更多信息,将在每个实验步骤中提供文献和教程。
补给品
用于实验的工具和组件:
- 用于电路仿真的 SPICE
- 示波器- 使用 Siglent 的 SDS 1052DL+ 进行实验,但也可以使用其他测量方法。
- 信号发生器- Rigol 的 DG4102 用于实验,但任何更便宜的替代品都可以。
- Mathematica -可以使用任何其他计算环境,例如Matlab 。
- PCB 制造商- PCB 板通过 JLC PCB 订购,但可以使用任何其他公司。随意货比三家。
- 模拟示波器可用于进一步了解电路的混乱行为。
电子元件:
- 运算放大器TL082(2 个运算放大器/IC)或TL084(4 个运算放大器/IC)
- 电阻器22Kohms - 220Ohms - 2.2Kohms - 3.3Kohms - 1Kohms - 100Ohms
- 电容0.1uF - 0.01uF
- 电感器18mH (Bourns)或18mH (Fastron)
- 电位器2Kohms或2.5Kohms
- 9V 电池连接器
- 滑动开关
- 电源插孔连接器
- BNC 连接器
第 1 步:Mathematica 中的理论
目标:
1) 非线性共振的已知形式是什么?
2) 用于描述和解释蔡氏电路共振的参数是什么?
建立计算环境
1)访问 Mathematica --> Mathematica 15 天试用
2)输入您的信息后,将向您发送一封电子邮件,为您提供激活密钥。如果您尚未在计算机上下载 Mathematica 软件,电子邮件中也会提供下载链接。或者,您可以利用云环境来编译笔记本。
3)从Github 项目存储库(ResonanceTheory.nb) 下载 Mathematica 笔记本。请注意,笔记本是理论思想的实验场所,因此在不断进步。因此,每个示例的代码可能并不总是最优的。
4)通过笔记本探索与各种非线性共振响应配对的动力系统的定量解释。随意尝试各种参数以获得进一步的见解。
*** 关于 Wolfram 语言的更多信息可以在 Wolfram文档中心找到。
分析的讨论和结论
现在已经在 Mathematica 中获得了一些理论直觉,让我们得出一些初步结论。
1) 已知的共振类型
- 随机共振
噪声引起的现象
量化方法:频率响应 (Q)、平均驻留时间、开关率、信噪比 (SNR)
当需要精度时,直观地假设噪声会分散和干扰。然而,随机共振证明相反。如果双稳态系统受到频率为 W 和最小振幅 A 的外部周期力,系统将无法在一个稳定平衡和缺乏外部能量之间交替。然而,当将噪声添加到外部周期力时,在输入频率 W 处测量的信噪比变得最大。结果,系统周期性地从一个电位平衡跃迁到另一个电位平衡。这种噪声作用被称为随机共振。
- 振动共振
高频力现象
量化 --> 频率响应 (Q),平均等待时间 (Tmw)
与随机共振相反,振动共振不需要双稳态系统来引发最大响应。换句话说,振动共振可以在可能平衡状态高于两个的动态系统中引起。在随机共振中发现的噪声项被高频力所取代,该力允许系统在相空间中广泛地从稳定和冒险过渡。这种由高频力引起的转变通常与可兴奋系统(如生物组织)的最大响应有关。
- 幽灵共鸣
意外频率现象
量化 --> 频率响应 (Q),平均等待时间 (Tmw)。
如果将随机共振和振动共振的基本原理结合起来会怎样?令人惊讶的是,将两个周期性力与噪声阈值相结合,会在输入驱动力缺失的频率处产生最大响应。即,输出信号以输入中不存在的频率放大。因此,鬼频率响应可以由噪声强度(鬼随机共振)或高频力(鬼振动共振)触发。
- 相干共振
孤独的噪音现象
量化 --> 功率谱、时间相关函数、脉冲之间的时间 (Tp)、偏移时间 (Te)、激活时间 (Ta)
相干共振与随机共振具有相似性。添加达到特定阈值的小噪声强度会引起系统的最大幅度响应。与随机共振相反,相干共振不需要周期性的力。只有噪声能够在动力系统上引起共振。
- 自共振
锁相现象
量化:频率扫描速率/啁啾速率
自共振产生于具有随时间变化的频率的外部驱动力。具体而言,从动系统不断调整其振荡幅度,使振荡周期与驱动力周期保持“锁相”。结果,系统被迫达到极高的幅度。令人惊讶的是,即使系统的参数发生变化,自谐振的锁相机制也会发生。事实上,参量自谐振也可以只作用于一个或多个系统参数。因此,系统在自谐振下的行为变得依赖于外部驱动力。人们可能想知道观察远距离系统之间的锁相现象的可能性。
- 参数共振
系统参数的定期更改
量化:功率谱、频率响应 (Q)
参量共振的特性与其他需要外部驱动力的共振有着根本的不同。当参数共振的一个或多个系统参数随时间周期性变化时,会出现最大幅度响应。例如,当变化率达到特定阈值时,具有呈现周期性变化的固有频率的系统将具有最大幅度响应。参量共振也可能来自其他参数的周期性,例如刚度、阻尼、密度等。
***请注意,提供的示例只是可能发生共振的一小部分。此外,这些示例没有采用振荡器系统的量子物理学解释,这使得许多令人惊讶的现象成为可能。对于想要了解更多信息的好奇者,可以在这里找到一本提供有关理论和广泛实验观察的深入信息的书。
2) 感兴趣的参数
解释蔡氏电路系统中共振的感兴趣的参数可以分为两类。一组描述电路行为(系统)的参数和描述输入信号(力)的参数。
系统参数:
描述随时间变化的电路状态的参数可以根据发现在电子电路中发生混沌所必需的三个标准进一步分类。* :
1)一个或多个非线性元件 --> Chua's Diode 组成:
- 运算放大器
在提供的方程中找到的参数M0和M1的值来自不同的设计配置,并且对于描述电路的非线性特性变得至关重要。
2)一个或多个本地有源电阻(蔡氏二极管子电路内的负电阻):
- 电阻器R1、R2、R3、R4、R5、R6
3)三个或更多储能元件:
电感L1
电容C1
电容C2
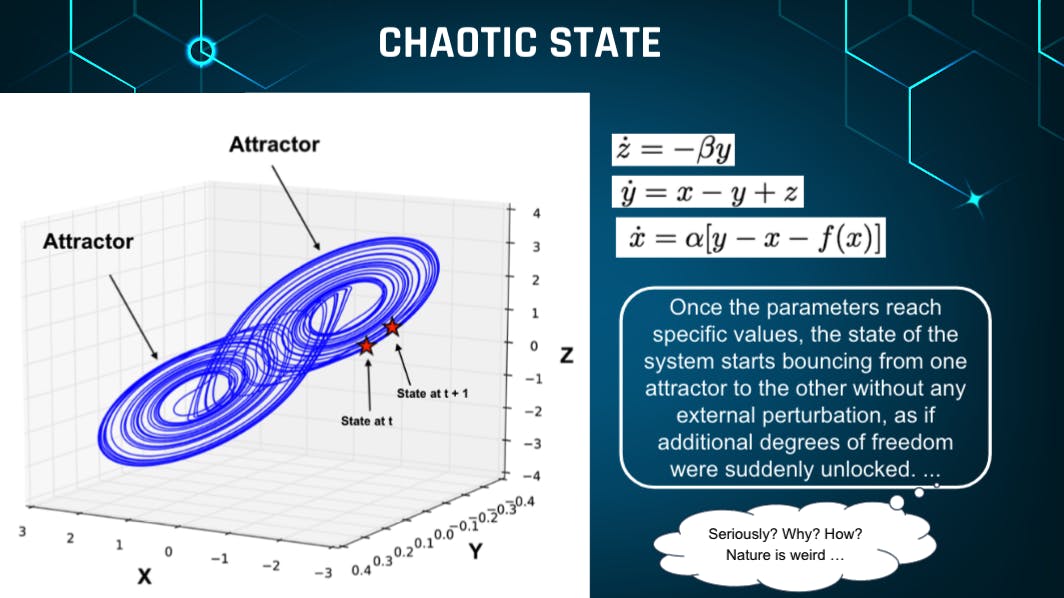
总之,电路的动态状态变得可以用三个变量来描述:
- 电容器 C1 两端的电压 = (V1) 或 (X)
- 电容器 C2 两端的电压 = (V1) 或 (Y)
- 电感 L1 上的电流 = (I) 或 (Z)
电路的时间演化由提供的视觉效果中的三个常微分方程描述。此外,电阻器的非线性特性在数学上由函数f(V1)表示,根据所选择的电路配置,该函数可能具有不同程度的复杂性。
*** 深入的理论讨论与实验证明了从线性 RLC 电路到非线性 Chua 电路的演变,能够进行混沌行为,可以在这里和这里找到。另一个有用的资源提供有关蔡氏电路实施的理论见解,可在以下内容中找到
肯尼迪93b.pdf
肯尼迪93.pdf
输入信号参数
现在已经确定了描述 Chua 电路的动态行为和已知谐振类型的系统参数,让我们澄清在选择输入信号的属性时要考虑的参数。正如您现在可能已经推断的那样,输入参数的范围根据各种类型的共振进行分类。
随机共振--> 周期性力与噪声配对。
- 幅度 (A1)
- 频率(f1)
- 噪声方差/强度 (D)
** 可能需要附加参数来表示复杂的噪声函数。
Vibrational Resonance --> 双谐波力由低频力和高频力组成。
- 幅度 (A1)
- 频率 (f1) 其中 (f1 < f2)
- 幅度 (A2)
- 频率 (f2) 其中 (f2 > f1)
Ghost Resonance --> 与噪声项配对的周期性力的总和。
- 幅度 (An) - 其中 n 取决于力的数量。
- 频率 (fn) - 其中 n 取决于力的数量。
- 噪声方差/强度 (D)
** 引起鬼共振的外部信号可能具有不同程度的复杂性。可能需要附加参数。
Coherence Resonance --> 仅噪声项。
- 噪声方差/强度 (D)
** 噪声可以以不同程度的复杂性引起,因此可能需要额外的参数。
Autoresonance --> 驱动力的频率随时间变化。
- 幅度 (A1)
- 时间相关频率 (f(t))
** 力频率的演变可以以多种形式出现,并且可能需要额外的参数。
参数共振——>没有外部扰动。
感兴趣的参数描述了系统参数的时间演变,而不是外部扰动。
- 自然频率的时间演化 (w(t))
- 采样的时间演化 (d(t))
*** 因此,动态系统可能表现出的各种可能的复杂性可能需要额外的参数。
第 2 步:使用 LTSpice 进行电路仿真
目标:
1) 哪些输入信号参数可以在蔡氏电路系统中引起振动共振?
2) 需要哪些信号分析技术来解释电路的响应?
*** 本节不作为 LTSPICE 教程,主要侧重于描述项目期间遵循的程序。但是,如果希望进一步了解LTSPICE提供的功能,下面提供了教程和资源的链接。
LTSPICE 资源:
LTSPICE_SIMPLE-STEPS-TO-IMPORT-THIRD-PARTY-MODELS.pdf
制作仿真 NETLIST / 电路图
幸运的是,LTSpice 带有友好的用户界面,允许使用传统电子元件制作原理图,而无需通过计算机代码表示电路:
1)在电路图工作空间内收集必要的组件:
- 两个 22Kohms 电阻。
- 两个 220 欧姆电阻。
- 一个 3.3Kohms 电阻。
- 一个 2.2Kohms 电阻。
- 一个 2.0K 电阻。(电位器)
- 一个 10nF 电容器。
- 一个 100nF 电容器。
- 一个 18mH 电感。
- 两个电压输入。
- 一地。
- 运算放大器:由于 LTSPICE 中的默认库中没有 TL082,因此可以使用 LT1057 或 LT1113 来模拟电路。或者,可以在设计环境中下载和导入 TL082 的 SPICE 模型。可以在此处和此处找到有关导入模型时要遵循的程序的更多详细信息。此外,可以从这里下载已经使用 TL082 设计的 Chua 电路(非常有见地的资源)。
添加第三方模型到 SPICE.pdf
LTSPICE_SIMPLE-STEPS-TO-IMPORT-THIRD-PARTY-MODELS.pdf
2)按照提供的 Chua 设计连接每个组件。此外,确保为每个组件分配正确的值。
3)由于代表电路状态的相关参数是电容器 C1、电容器 C2 两端的电压和电感器 L 两端的电流,因此相应地添加了电压探针。
4)现在让我们探讨改变位于电容器 C1 和电容器 C2 之间的电阻器 R7 的值的影响。一旦达到特定的电阻阈值,电路就会表现出混乱的行为。为了观察双涡旋混沌特征,电容 C1 两端的电压 (V(vc1) probe) 必须绘制在水平轴上,电容 C2 两端的电压 (V(vc2)) 绘制在垂直轴上。
仿真参数设置如下:
类型:瞬态
-停止时间: 0.10
-开始保存数据的时间: 0
-最大时间步长: 1E-5
从仿真中获得的混沌签名证实了生成的网表符合 Chua 的电路特性。R7 引起的最佳混沌行为的电阻值似乎集中在 1.5KOhms 左右。然而,当电阻值低于 1.485 KOhms 和高于 1.965 KOhms 时,系统的动态会发生剧烈变化。尽管本仿真的目的不是研究混沌,但请随意探索 R7 的电阻值如何影响电路的混沌行为。
在 LTSPICE 中观察共振
以下程序将主要侧重于探索振动共振,以尽量减少项目的长度。但是,也可以通过调整输入信号参数来研究其他类型的谐振。(A1, f1, A2, f2)
振动共振(高频力)
振动共振的作用是通过添加高频(f2)周期力(F2)在与低频驱动力(F1)的外部频率(f1)匹配的频率处发现的输出信号的增强幅度.
模拟参数:
-类型:瞬态
-停止时间: 100 毫秒
-开始时间: 50ms
-最大时间步长: 1*10^-5
系统参数:
为模拟选择的系统参数可以从提供的模拟示意图中得出。
输入参数:
力量 1 (F1)
- 幅度 (A1) = (0.3 V, 0.8 V, 1.3 V, 1.8V)
- 频率 (f1) 必须 <(f2) = (50 Hz, 100 Hz, 150 Hz, 200 Hz)
力量 2 (F2)
- 幅度 (A2) = (0.5 V、1.5 V、2.5 V、3.5 V)
- 频率 (f2) 必须 >(f1) = (500 Hz, 1500 Hz, 2500 Hz, 3500 Hz)
预期结果/假设:
- 在快速傅里叶变换分析 (FFT)下,当参数 (A2) 和 (f2) 达到特定值时,频率匹配 (f1) 处的输出信号幅度将最大化。
- 在幅值响应分析下,只有当参数(A1)、(A2)、(f1)、(f2)达到特定阈值时,输出信号的幅值才会达到最大值。
- 在时间序列分析下,电容器 1 (V1) 两端的电压状态将在 (V1 < 0) 和 (V1 > 0) 之间周期性切换,其周期等于频率 (f1) 周期的一半,一旦参数 (A2) 和 ( f2) 达到特定值。
观察:
快速傅里叶变换 (FFT) 分析:
1)随着参数 (f2) 从 500 Hz 增加到 3500 Hz,每增加 1000 Hz,输出信号 (V1) 在 (f1 = 100Hz) 的幅度在 (f2) 等于 1500 Hz 时达到最大值。
2)随着参数 (A2) 从 0.5 V 增加到 3.5 V,增量为 1.0 V,输出信号 (V1) 在 (f1 = 100 Hz) 的幅度在 (A2) 等于 0.5 V 时达到最大值。
3)随着参数 (f1) 从 50 Hz 增加到 200 Hz,增量为 50 Hz,当 (f1) 达到 200 Hz 时, (f1) 处的输出信号 (V1) 的幅度达到最大值。
4)随着参数 (A1) 从 0.3 V 增加到 1.8 V,增量为 0.5 V,输出信号 (V1) 在 (f1 = 200 Hz) 的幅度在 (A1) 等于 1.8 V 时达到最大值。
幅度响应 (Q) 分析:
- 收集以 dBV 为单位报告幅度的 FFT 数据。
- 将幅度从 dBV 转换为 V。 (V = 10exp(dBV / 20))
- 计算幅度响应 (Q),其中 Q = (输出幅度 (V) / 输入幅度 (A1))
1)第一次分析获得的结果与模拟期间获得的数据相关。具体而言,响应振幅Q在高频力值(f2)为1500Hz左右时达到最大阈值。
2)同样,在第二次幅度响应分析期间获得的结果表明,幅度响应 Q 随着高频力(A2)的幅度减小而增加。
*** 用于从 LTSpice 收集模拟结果并生成幅度响应图的 Excel 表可在此处下载。可以遵循相同的分析程序,以进一步了解其他参数的最佳值。
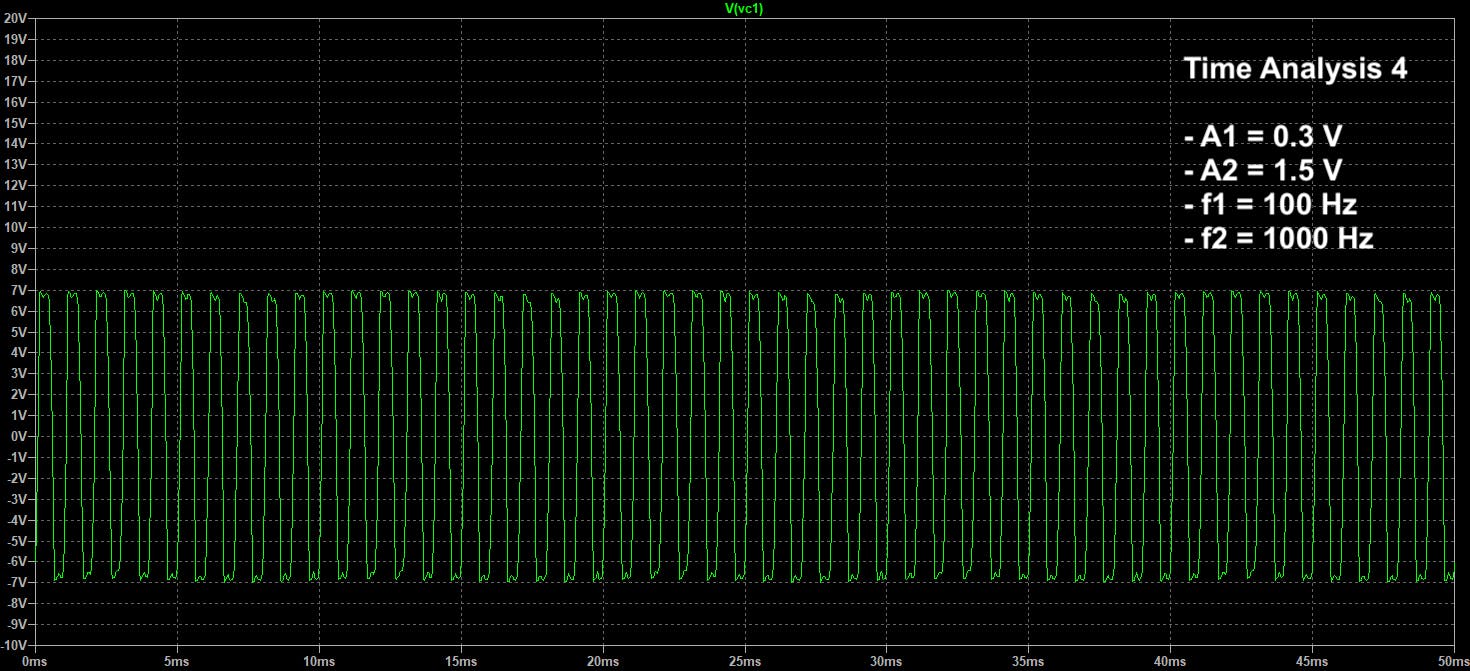
时间序列分析:
随着高频力 (A2) 的幅度从 0.00V 增加到 1.50V,系统经历从 V1 < 0 和 V1 > 0 的周期性切换。计算 V1 = + 和 V1 = - 的平均停留时间证明一旦 (A2) 达到临界值,MRT+ 就等于 MRT-。此外,在 (A2) 这样的临界值下,V1>0 和 V1<0 之间的周期性切换变为低频力周期的一半(周期性切换 = 1/2*(1/f1))。
*** 可以在此处获得有关振动共振时间序列特征的更多信息。
第 3 步:硬件设计和组装

目标:
1) 使用Eagle设计 Chua 的电路 PCB 。
2) 将制造文件提供给JLC PCB进行生产并从Mouser订购所需的组件。
3) 组装电路。
Eagle 通用教程链接:
如需进一步了解 Eagle 的功能,请随时浏览下面的教程链接。
Eagle中的电路原理图
1)在 Eagle 主页的项目部分下创建一个新文件夹。
2)通过右键单击项目文件夹并选择 NEW --> SCHEMATIC 创建原理图设计文件。
3)创建新原理图时的第一个任务是在设计工作区中导入一个框架。选择 ADD-PART 按钮并搜索框架库。(FRAME_A_L 尺寸为 8 1/2 * 11 英寸,景观)被选中用于该项目。
4)现在必须从可用的库中选择所需的电子元件并将其导入设计工作区。选择 ADD-PART 按钮并收集组件以重现 Chua 的电路设计。可以在此处访问项目期间使用的所有组件的列表。
*** 请注意,也可以使用来自其他库的不同组件。由于我们没有在 eagle 内部进行任何模拟,因此选择组件时的关键标准是确保封装和封装类型与从电子供应商订购的组件相匹配。不这样做会导致将芯片焊接到 PCB 板上时遇到困难,因为焊针布局与这些组件不匹配。
5)为所有组件分配名称和值。
6)按照 Chua 的电路设计连接每个组件,继续创建电路原理图。
PCB布线和制造
1)连接组件并完成电路图后,单击 GENERATE/SWITCH TO BOARD 按钮以生成 PCB 布局工作区。
2)为了控制电路板布局和尺寸,Fusion 360 用于设计过程。
3)在 Fusion 360 中完成 PCB 布局后,单击右侧的 FUSION 360 垂直按钮将其导入 Eagle 的 PCB 布局工作区。可以在此处找到有关从 Fusion 360 导入 PCB 所需程序的更多见解。
4)在 Eagle 环境中拥有所有组件和所需的 PCB 布局后,我们必须将每个组件放置到 PCB 板上。为了简化布线过程,请确保每个组件的位置遵循原理图的逻辑。
5)连接元件的每根空气线必须走线到 PCB 表面。您可以手动路由每个连接,也可以使用自动路由选项让 EAGLE 自动创建所有连接。鉴于原理图的简单性,我们使用手动布线来确保所有引脚都正确布线。此外,还创建了一个多边形来为所有组件提供集体地面。有关路由方法以及创建多边形的更多信息,请参见此处。请注意,在继续下一节之前,可以删除或添加 PCB 板上的文本以进行描述。
6)一旦完成所有布线连接,我们将审查所有设计参数以确保 PCB 布局产生预期的输出。此外,必须调整制造参数以符合制造厂的要求。有关最终确定设计参数和生成所需的 Gerber 文件以进行制造的程序的所有详细信息,都可以在此处找到。
7)生成 Gerber 制造 ZIP 文件后,必须选择制造商来订购电路板。有关要考虑的制造选项的更多详细信息,请参见此处。对于当前项目,Gerber 文件已上传到JLC PCB 订购页面。
组装电路
- 考虑到组件的尺寸,需要使用显微镜将组件适当地焊接到 PCB 上。或者,您可以在从 JLC PCB 订购 PCB 时选择 SMT 组装选项,并让他们为您组装所有组件。更多细节可以在这里找到。
- 运算放大器 IC 的 + 和 - 引脚不易察觉。因此,请确保在电位器的另一侧以水平方向的基准线焊接 IC。
- 焊接电位器时,利用左中针将增加旋钮顺时针旋转时的电阻。相反,当旋钮逆时针旋转时,使用右侧和中间销会增加阻力。
*** 由于目前的研究项目正在进行中,未来将在Github 项目存储库上提供不同的电路配置。
第 4 步:实验
目标:
1) 电位器两端需要什么电阻值来观察电路中的混沌行为?
2)高频力(F2)的幅值(A2)如何影响振动共振下电路的时序演化?
观察混沌:
1)将示波器的通道#1 连接到电路的输出 1,报告电容器 C1 上的电压。
2)将示波器的通道#2 连接到电路的输出 2,报告电容器 C2 上的电压。
3)将两节 9V 电池连接到各自的电池插孔。
4)将示波器设置调整到 XY 模式,在 X 轴上绘制电容器 C1 两端的电压和电容器 C2 两端的电压。
5)调整各轴的刻度,直到测量分辨率合适。
6)慢慢转动电位器的旋钮,找到合适的电阻值,以使混沌行为发生。如果您有任何不稳定的连接或不正确的电位器电阻,此过程可能会非常繁琐。
7)虽然不是最精确的方法,但万用表可以测量电位器感应的电阻值。
混沌测量#1:
电阻值 (R) = 1.194 KOhm
水平轴 (V1) = 100 mV/格
垂直轴 (V2) = 500 mV/格
混沌测量#2:
电阻值 (R) = 0.750 KOhm
水平轴 (V1) = 50 mV/格
垂直轴 (V2) = 500 mV/格
混沌测量#3:
电阻值 (R) = 1.240 KOhm
水平轴 (V1) = 100 mV/格
垂直轴 (V2) = 500 mV/格
混沌测量#4:
电阻值 (R) = 1.220 KOhm
水平轴 (V1) = 200 mV/格
垂直轴 (V2) = 1.00 V/div
观察与讨论
示波器在 XY 模式下生成的电路的状态空间表示允许通过在 X 轴上绘制电容器 C1 两端的电压和在 Y 轴上绘制电容器 C2 两端的电压来分析电路的动态行为。您可以将示波器 XY 图中的一个小点想象为任意时间 T 的电路状态。随着时间的推移,状态测量值(点)的集合产生了一个几何表示,其中系统的状态演变产生几何图案。例如,从电阻值约为 1.194 KOhm 的测量 #1 中,我们观察到系统通过总共四个不同的轨道围绕平衡点运行的状态。随着电位器上的电阻值接近在电路中引起混乱所需的阈值,轨道数增加,该阈值约为 1.220 KOhm。正如在测量#4 中观察到的,系统在混沌行为下的状态可以从正轨道跳到负轨道。从理论上讲,一组特定的参数值,其中状态从一个吸引子到另一个吸引子的动态演变变得完全“随机”。令人惊讶的是,这种混沌特性对许多应用程序(例如密码学)很有用。可以找到关于蔡氏电路中混沌演变的进一步理论见解 从理论上讲,一组特定的参数值,其中状态从一个吸引子到另一个吸引子的动态演变变得完全“随机”。令人惊讶的是,这种混沌特性对许多应用程序(例如密码学)很有用。可以找到关于蔡氏电路中混沌演变的进一步理论见解 从理论上讲,一组特定的参数值,其中状态从一个吸引子到另一个吸引子的动态演变变得完全“随机”。令人惊讶的是,这种混沌特性对许多应用程序(例如密码学)很有用。可以找到关于蔡氏电路中混沌演变的进一步理论见解这里和这里。
两个涡旋吸引器之间的尺寸差异是由于输入功率不对称造成的。具体来说,当电池正负输入源之间的电压差很小时,就会出现不对称。例如,一个电池提供的负功率可能比正输入的幅度小 0.7 V。因此,可以利用电源通过运算放大器的输入施加 9V 和 -9.7V 来补偿功率差。
此外,电路中使用的二极管类型对于发生混乱至关重要。大范围的二极管导致无法观察到电路中的任何混乱行为。发现 Fastron的18mH 5% 电感器可实现最佳结果。
振动共振实验:
1)将信号发生器的通道#1 连接到电路的输入插孔#1。
2)将信号发生器的通道#2 连接到电路的输入插孔#2。
3)将示波器的通道#1 连接到电路的输出#1,报告电容器C1 上的电压。
4)将示波器的#2 通道连接到电路的#2 输出,报告电容C2 两端的电压。
5)确保电路安装牢固,避免测量过程中连接松动。
6)将两节 9V 电池连接到各自的电池插孔。
7)将示波器设置为更多时间序列,并简单地调整每个轴的刻度以及采样率,直到您可以观察到通道#1 和通道#2 的清晰正弦波。
8)对于时间序列分析,我们希望一次测量一个通道输出以最大限度地提高清晰度。因此,关闭示波器上的通道#1 显示。
9)将电位器的阻值调整为1.350 KOhm。
*** 为了尽量缩短项目的长度,将仅探讨高频力 (F2) 的幅度 (A2) 的影响。此外,将仅介绍输出信号的时间序列分析。将示波器模式调整为 FFT 可以探索输出信号的频率分量。随意尝试不同的输入参数和测量方法。
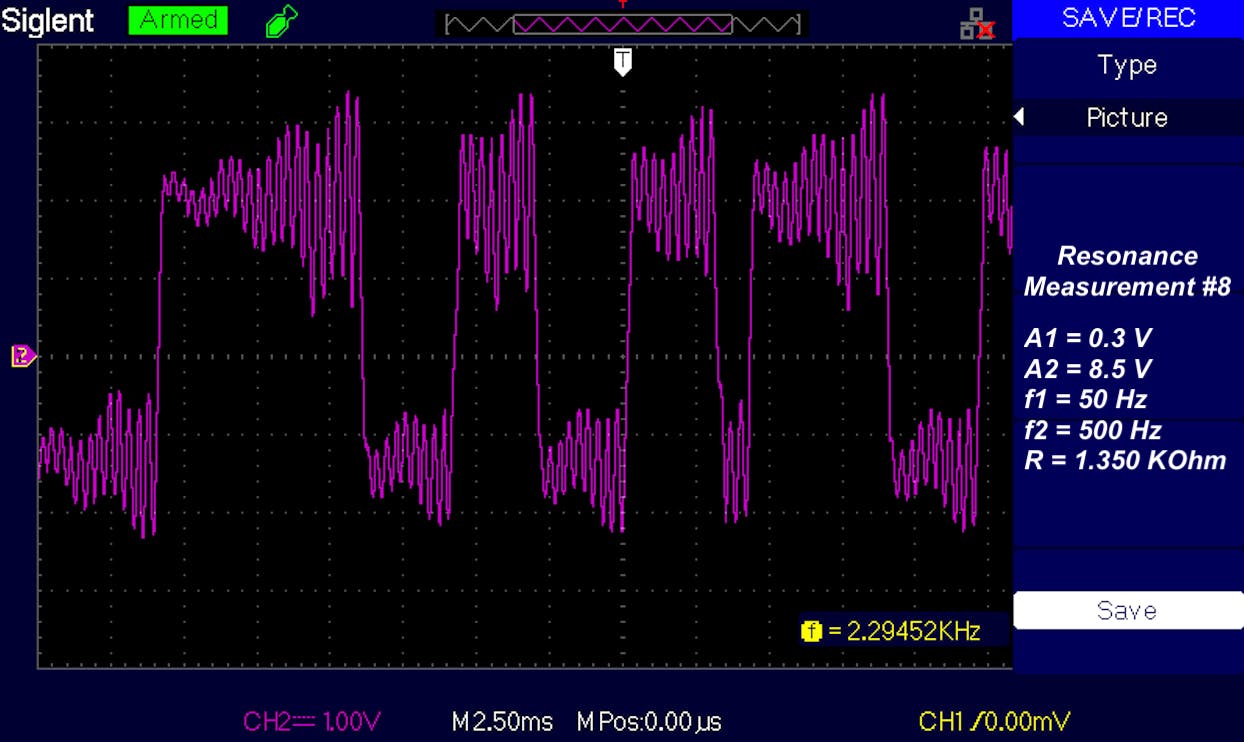
共振测量 [#1 - #8]
电阻值(R):R = 1.350 KOhm
输入信号参数:
CH1(力 #1)幅度 = 0.3 V
CH1(力#1)频率 = 50 Hz
CH2(力 #2)幅度 = [0.0 V - 3.5 V - 4.5 V - 5.5 V - 6.5 V - 7.5 V - 8.5 V]
CH2(力 #2)频率 = 500 Hz
观察与讨论:
一旦达到 (A2) 的阈值,系统就可以从正值跳转到负值。系统在正负区域所花费的时间称为停留时间(T+,T-)。考虑一段时间内的所有停留时间,我们可以计算平均停留时间(Tmr+,Tmr-)。在测量编号 #3 中,阳性 (T+) 和阴性 (T-) 之间的平均停留时间差异很大。与在正区域中花费的时间相比,发现系统在短时间内输出负值。随着输入幅度 (A2) 从测量 #3 中的 4.5 V 增加到测量 #8 中的 8.5 V 幅度 (A2),正平均停留时间 (Tmr+) 和负平均停留时间 (Tmr- ) 被发现减少。对于幅度的特定阈值 (A2_max),正值和负值之间的平均停留时间变得相等。进一步的分析可以证明,在幅度值等于 (A2_max) 的情况下,从正区域到负区域的周期性切换发生的周期等于低频输入 (f1) 周期的一半。正是在这样的输入阈值下才会发生振动共振。给定为实验选择的参数,发现 A2_max 约为 8.5V。与模拟期间获得的结果相比,电压阈值相对较高可能是由于在实验期间将电阻值 (R) 设置为 1.350 KOhm。此外,可以计算幅度响应分析以找到接近 8.5V 的值范围内的 A2_max 的特定值。正值和负值之间的平均停留时间变得相等。进一步的分析可以证明,在幅度值等于 (A2_max) 的情况下,从正区域到负区域的周期性切换发生的周期等于低频输入 (f1) 周期的一半。正是在这样的输入阈值下才会发生振动共振。给定为实验选择的参数,发现 A2_max 约为 8.5V。与模拟期间获得的结果相比,电压阈值相对较高可能是由于在实验期间将电阻值 (R) 设置为 1.350 KOhm。此外,可以计算幅度响应分析以找到接近 8.5V 的值范围内的 A2_max 的特定值。正值和负值之间的平均停留时间变得相等。进一步的分析可以证明,在幅度值等于 (A2_max) 的情况下,从正区域到负区域的周期性切换发生的周期等于低频输入 (f1) 周期的一半。正是在这样的输入阈值下才会发生振动共振。给定为实验选择的参数,发现 A2_max 约为 8.5V。与模拟期间获得的结果相比,电压阈值相对较高可能是由于在实验期间将电阻值 (R) 设置为 1.350 KOhm。此外,可以计算幅度响应分析以找到接近 8.5V 的值范围内的 A2_max 的特定值。进一步的分析可以证明,在幅度值等于 (A2_max) 的情况下,从正区域到负区域的周期性切换发生的周期等于低频输入 (f1) 周期的一半。正是在这样的输入阈值下才会发生振动共振。给定为实验选择的参数,发现 A2_max 约为 8.5V。与模拟期间获得的结果相比,电压阈值相对较高可能是由于在实验期间将电阻值 (R) 设置为 1.350 KOhm。此外,可以计算幅度响应分析以找到接近 8.5V 的值范围内的 A2_max 的特定值。进一步的分析可以证明,在幅度值等于 (A2_max) 的情况下,从正区域到负区域的周期性切换发生的周期等于低频输入 (f1) 周期的一半。正是在这样的输入阈值下才会发生振动共振。给定为实验选择的参数,发现 A2_max 约为 8.5V。与模拟期间获得的结果相比,电压阈值相对较高可能是由于在实验期间将电阻值 (R) 设置为 1.350 KOhm。此外,可以计算幅度响应分析以找到接近 8.5V 的值范围内的 A2_max 的特定值。与模拟期间获得的结果相比,电压阈值相对较高可能是由于在实验期间将电阻值 (R) 设置为 1.350 KOhm。此外,可以计算幅度响应分析以找到接近 8.5V 的值范围内的 A2_max 的特定值。与模拟期间获得的结果相比,电压阈值相对较高可能是由于在实验期间将电阻值 (R) 设置为 1.350 KOhm。此外,可以计算幅度响应分析以找到接近 8.5V 的值范围内的 A2_max 的特定值。
*** 请注意,目前的研究项目仍在进行中,未来有关实验的更新将添加到Github 项目页面和研究门。
第 5 步:总结 - 结论 - 未来方向

概括
本项目共同为未来使用 Chua 电路作为实验系统研究非线性谐振的实验奠定了基础。以下是项目期间得出的初步结论的摘要:
理论
总共审查了六种不同类型的共振:
- 随机共振(周期性力与噪声配对)
- 振动共振(高频双谐波力)
- 相干共振(仅噪声)
- 鬼共振(双谐波力与导致意外输出频率的噪声配对)
- 参数共振(周期系统的参数)
- 自动共振(外力锁相)
蔡氏电路的时间演化是用三个感兴趣的参数和三个常微分方程建模的:
- 电容器 1 两端的电压(V1)
- 电容器 2 两端的电压(V2)
- 电感器上的电流(L)
模拟
对于选择的模拟参数,发现特定的输入值会在振动共振下引起电路的最大幅度响应:
- 强制 1 幅度 (A1):1.8 V
- 力 2 幅度 (A2):0.5 V
- 强制 1 频率 (f1):200 Hz
- 力 2 频率 (f2):1500 赫兹
报告了三种类型的信号分析方法来解释电路的谐振响应:
- 快速傅里叶变换 (FFT) 分析:允许将输出信号分解为其频率分量。
- 幅度响应分析 (Q):允许导出一系列输入参数的最大幅度值。
- 时间序列分析:允许观察系统随时间的演变。
硬件设计
选择了以下电子元件属性:
电容器 C1:100 nF
电容器 C2:10 nF
电感器 L:18 mH
可变电阻器 R:2 KOhm
电阻器 R2:220 欧姆
电阻 R3:220 欧姆
电阻 R4:2.2 KOhm
电阻 R5:22 KOhm
电阻 R6:22 KOhm
电阻 R7:3.3 KOhm
运算放大器:TL082
实验
在选定的实验参数下,发现电路的混沌行为发生在特定电阻值为:
- 电阻值 (R) = 1.220 KOhm
在振动共振下,发现正负值之间的周期性切换是由高频力的阈值幅度值引起的:
- 力 2 幅度 (A2) = 7.5 V (+- 1.0V)(近似解)
未来发展方向
- 通过探索各种输入参数来探索蔡氏电路中其他类型的共振。例如,在蔡氏电路系统中是否可以观察到其他类型的非线性谐振?
- 研究按照不同网络拓扑耦合的多个 Chua 电路之间的谐振输入信号的传播。每个耦合系统的状态演化将如何随时间变化?例如,受输入信号影响的电路的最大响应幅度是否会间接感应网络中的其他系统?
- 探索生物系统中的共振。鉴于生物有机体的非线性特性,Chua 电路的共振响应与生命系统对外部刺激的响应之间是否有相似之处?非线性共振背后的原理能否让我们进一步了解允许生物体之间进行远程通信的物理机制?
- 将非线性共振变为实用性。在未来的设计中如何利用非线性共振来解决实际问题?
“如果你想发现宇宙的秘密,请从能量、频率和振动的角度来思考。” - 尼古拉·特斯拉。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章




