
资料下载

嫦娥三号软着陆轨道设计与控制策略
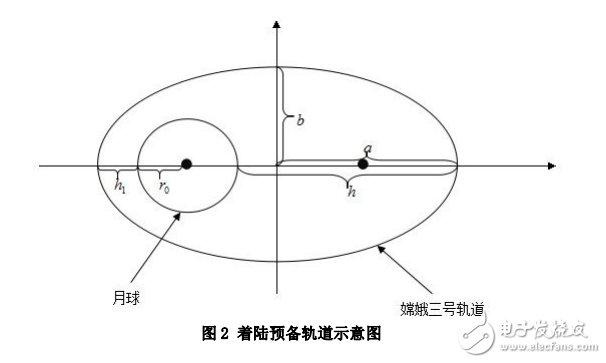
嫦娥三号是中国发射的第一个地外软着陆探测器和巡视器(月球车)。它的发射对我国航天事业具有重要意义。为解决嫦娥三号软着陆的轨道设计与控制策略问题,本文首先分析各项因素对嫦娥三号轨道的影响,基于合理假设简化模型,建立以月心为坐标原点的球极坐标系,为分析后续问题奠定基础。针对问题 1:考虑到探测器在着陆预备轨道上时距离月面距离较远,此时可将月球与探测器两者组成的系统问题视为两体问题。首先分析系统受力,建立着陆器的归一化质心运动方程,将着陆点满足的约束条件视为终端条件,近日点的约束条件作为初始条件,通过求解运动方程得到近日点与远日点的位置坐标。轨道确定后,根据开普勒第一定律与万有引力定律建立方程组,求得近日点和远日点速度分别为v 1692.30m/ s 0 和v 1614.01m /s 1 (其余轨道参数见表 1)。针对问题 2:为了满足主减速阶段燃料消耗最小的要求,首先将问题 1 中的运动方程表示为状态方程的形式,按照耗燃最小为优化目标构造哈密顿函数,根据 Pontryagin 极大值原理求出该阶段的最优推力进而确定最优制导率。根据初始条件与终端约束,将最优轨道问题转化成两点边值问题,使用计算机仿真求解,得到主减速阶段各项参数值随时间的变化(图 4)。考虑到快速调整阶段时间很短这一事实,基于该阶段的动力学方程,经过论证,可用主减速阶段的轨道参数计算方法求解这一阶段的轨道参数值。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章





