
资料下载

×
曲线的弧角概念及其应用
消耗积分:2 |
格式:rar |
大小:0.48 MB |
2018-02-26
给定一段曲线,如何从整体上评价它,或者说,给出哪些描述其整体特性的度量指标是一个有意义的问题。显然,最常用的指标是弧长,它是曲线展直后的总长度。数学上,弧长是曲线弯曲和扭曲下的不变量,应用中则可以表示诸如质点的曲线运动路程、弯曲公路的路程,以及漆包线中铜线的卷绕长度等,因此,是一个重要的概念。然而,弧长不能反映曲线的形状,因此还需要其它的度量指标。这些指标也已经存在,如反映曲线总弯曲的全曲率和反映曲线总扭曲的全挠率等与曲线曲率和挠率有关的指标。然而,这里有两个问题。第一,例如,全曲率这个名称可能不利于应用。我们知道,所谓曲线的曲率是其切矢对于弧长的旋转速度,是一个角速度的概念,而全曲率为曲率对于弧长的积分,结果是角度而不是角速度(两者量纲不同),但全曲率字面上容易被理解成仍然是一种曲率(角速度)。第二,例如,虽然全曲率的数学意义(特别是闭合曲线)得到了充分的发掘,但其应用(特别是非闭合曲线和工程应用)似乎没有得到充分的关注。
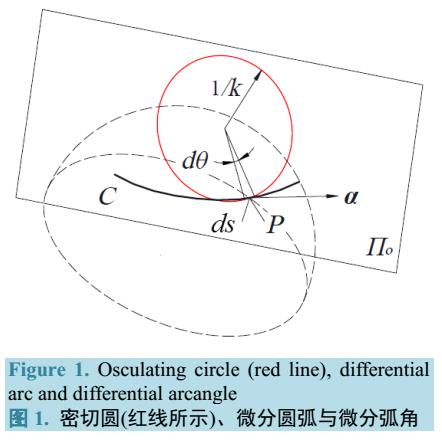
注意到,圆弧的全曲率等于其圆心角,也就是圆弧对于其圆心所张成的角度。圆心角在一些文献中被称为弧角(arcangle),恰好与圆弧的弧饫对应。显然,这个名称直观,便于应用。那么,可否将这个概念推广到一般曲线上?本文就这个问题进行了讨论。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
评论(0)
发评论
- 相关下载
- 相关文章
下载排行榜
- 暂无相关数据






