
资料下载

归一化在电机控制中究竟有什么用?(可下载)
大家好,今天我们来了解一下归一化在电机控制中的作用,那么首先我们需要先了解一下归 一化的概念,这样才能更好的了解电机控制中为什么会经常用到归一化。
归一化就是将一个数据变换到(0,1)或者(-1,1)之间的小数,这样的话把数据范围都统一了, 在一些算法处理中会更加方便,容易理解。
下面,我们举两个例子,这样可以更好的理解归一化,假设某个数据的变化范围是[0,1023],那么 我们知道这个数据范围的最小值(xmin)是 0,最大值(xmax)是 1023,若我们得到的一个数据为 x, 那么归一化的方式就可以表示为:

如果 x=1023,那么此时对 1023 归一化之后的结果为:
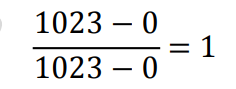
如果 x=500,那么此时对 500 归一化之后的结果为:
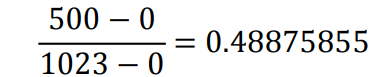
接着我们再来看如果某个数据的变化范围是[-1023,1023],那么对于大于 0 的部分的归一化方式跟 上面一致,归一化公式还是如下:
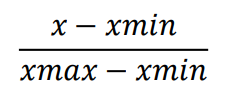
对于小于 0 的部分[-1023,0],归一化方式就可以表示为:
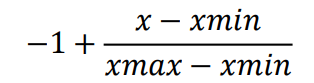
假设得到的数据 x 是-1023,那么可以得到此数据对应的归一化值为:
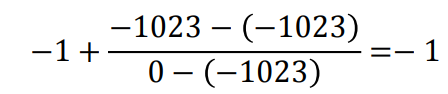
假设得到的数据 x 是-500,那么可以得到此数据对应的归一化值为:
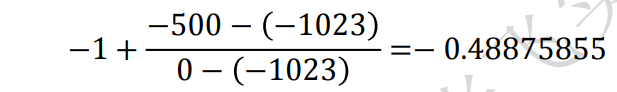
通过以上实例分析,我们知道了归一化的实际实现方式,当我们有其它数据需要归一化时,就可以 很容易的得到对应的归一化值。
在电机控制中,我们会对电角度进行归一化,我们都知道电角度的变化范围是 0 至 360 度,或者-180
至 180 度,那么,同样我们也有两种归一化方式,对于用 0-360 度范围表示的电角度来说,归一化方式
如下:
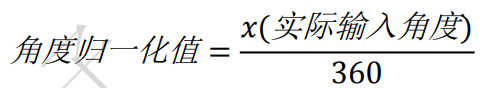
如果输入的角度是 360 度,那么得到的归一化值为 1,如果输入的角度是 180 度,那么归一化值就
是 0.5,其它角度可以根据上面的角度归一化公式进行计算,这样对于 0 至 360 度范围的值就可以变化
到 0 至 1 范围内了。
对于-180 至 180 度范围表示的电角度来说,归一化的方式如下:
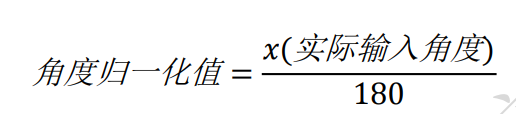
如果输入的电角度是 180 度,那么得到的归一化值为 1,如果输入的电角度是-60 度,那么得到的 归一化值为-0.333333333,这样对于-180 至 180 度范围的值就可以变化到-1 至 1 范围内了。
归一化弄清楚之后,通过归一化,可以得到 0 至 1 或者-1 至 1 之间的小数了,但是在电机控制中, 大多数的单片机都没有浮点运算单元,而电机控制的算法中会用到大量的乘法运算,如果对于没有浮点 运算单元的单片机来说,直接使用进行小数乘法或者小数除法,那么计算一个小数乘法或者计算一个小 数乘法需要花费的时间是很长的。
假设我们整个电机控制算法全部执行完毕需要的时间是 30us,那么如果一个小数乘法或者除法运 算就花费了几微秒或者几十微秒,整个电机控制算法的就可能无法在 30us 以内完成了,那么对于一款 没有浮点运算单元的单片机来说,又想实现小数乘法或者小数除法应该怎么做呢?
其实大部分的单片机有整数乘法,如果我们把小数乘法转化为整数形式乘法,那么也是可以实现小 数乘法运算的,而且整数乘法运算的速度是比较快的,大部分的单片机都是单指令周期就可以实现,那 么怎么实现把小数乘法转换为小数乘法呢?
接下来我们就要引入定点小数格式了,先给大家介绍一下定点小数格式的表示方法。
其定义为:约定单片机中所有数据的小数点位置是固定不变的。数据的最高位表示符号位,小数点 是隐含在符号位之后的。这种格式通常被称为 1.15 或 Q15 格式,1.15 中的 1 表示数据整数部分的位数, 而 15 表示小数部分的位数。
下面用一个图示给大家说明一下这个定点小数的数据格式啊。
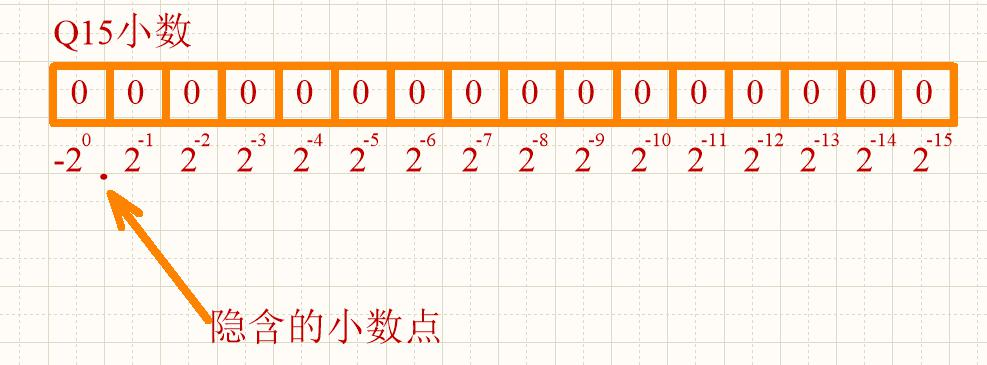
大家看这幅图啊。Q15 格式的话,就是对于一个 16 位数来说,把最高位作为符号位,然后小数点 是隐含在符号位后面的,剩余的 15 位作为数据位。
我们不妨根据上面这个数据格式来举例说明一下小数跟定点小数格式的转换方式,假设有一个数为 0.5,那么对应的定点小数格式表示就是:

对应的 16 位数据格式的 16 进制表示为 0x4000,十进制表示为 16384。也就是说,对于-1 至 1 范 围的小数来说,16384 表示 0.5。
我们再假设有一个数据为-0.3,那么通过定点小数格式表示为:

计算的方式为:
− 2 0 + 2 −1 + 2 −3 + 2 −4 + 2 −7 + 2 −8 + 2 −11 + 2 −12 + 2 −14 =− 0.29998779296875 ≈− 0.3
上图对应的 16 位数据格式的 16 进制表示为 0xD99A,十进制表示为-9830。也就是说,对于-1 至 1 范围的小数来说,-9830 表示-0.3。
以上是-1 至 1 之间小数(有符号小数)的定点小数格式表示方式,那么在电机控制中有时还会用 到无符号小数(0 至 1 之间的小数),这个时候其实就是将 Q15 格式表示中的符号位去掉,所有的位都 表示数据位,具体表示方式如下图所示:
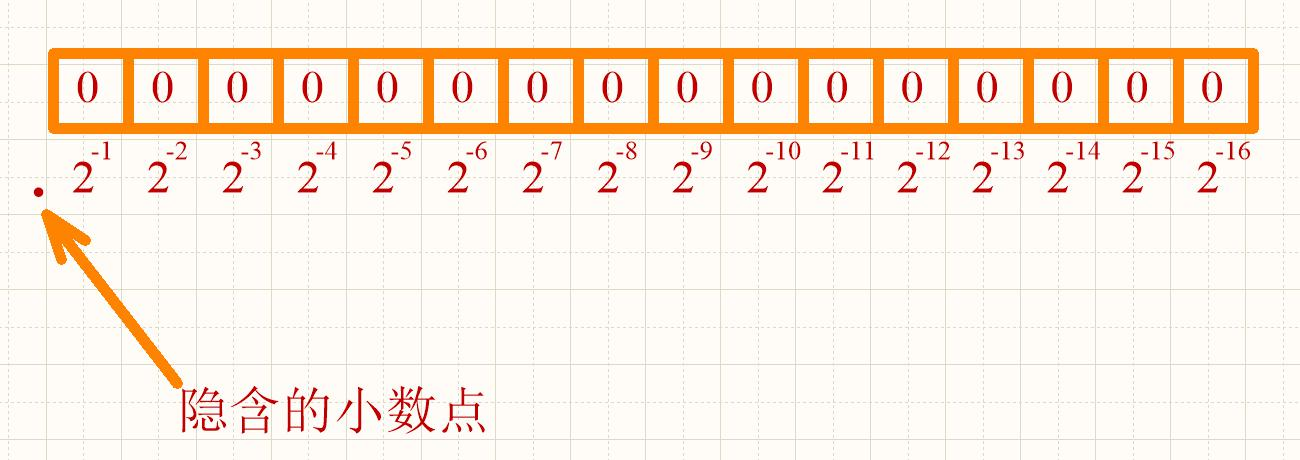
我们不妨也对这种表示方式举个具体的例子来说明一下,假设小数为 0.5,那么对应定点小数格式 就表示为:

上图对应的 16 位数据格式的 16 进制表示为 0x8000,十进制表示为 32768。也就是说,对于 0 至 1 范围的小数来说,32768 表示 0.5。
假设得到的小数为 0.7,那么对应定点小数格式就表示为:
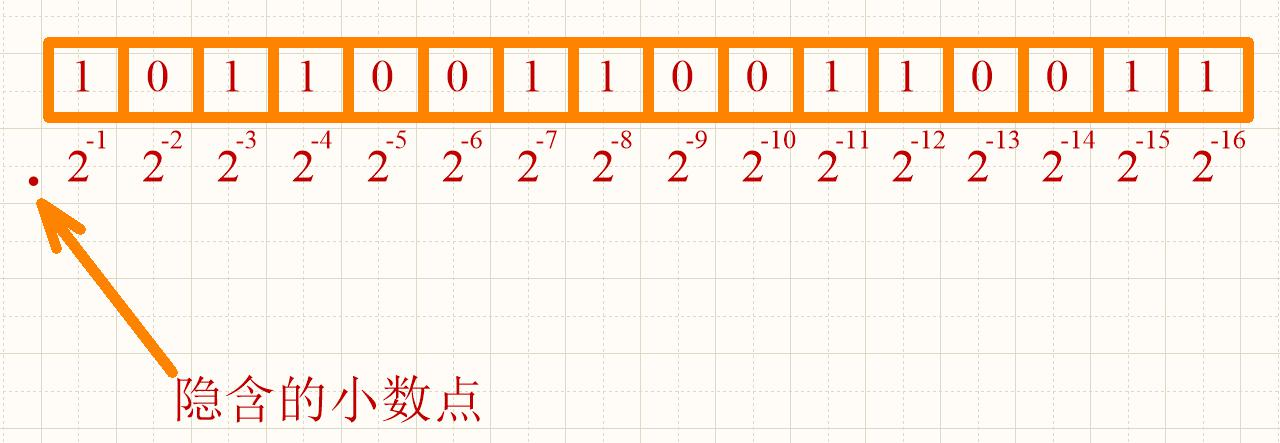
计算的方式为:
完整版的技术文档点击文章开头的普通下载
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章






