
资料下载

如何使用部分和分解进行二维DCT变换快速算法研究
离散余弦变换是广泛应用于信号处理、图像处理领域的重要工具之一,已经被多个国际标准所接受,如JPEG、MPEG、H.263 等。DCT应用到实际系统中的前提是具有能够快速实现的算法,自从1977年第一个真正的DCT快速算法出现以来,寻求更快、更规则、更简单的DCT快速算法一直 是信号处理领域的一个热点研究方向。
作为正交变换的DCT算法具有计算复杂度适中、快速算法等特点,在数字信号处理等方面有着广泛的应用。由于应用领域的不同,也出现了很多形式的DCT算法。
本论文主要研究的是二维离散余弦变换的快速算法设计,其研究的重点是实现二维DCT变换的直接分解算法。论文工作分为三个部分:
一。对DCT算法进行总结,概括和描述了近几年出现的DCT算法并进行分类。二。在研究已有DCT算法的基础上提出了一种改进的快速算法-部分和分解算法(PSDA算法);在PSDA算法中,通过引入部分和的定义,实现了频域输出数据的分集;通过频域输出数据的分集将二维DCT变换转换为若于个- -维DCT变换;PSDA算法还给出了部分和的计算方法及组成部分和的公共加法项的合并原则。
三。从VLSI实现的角度出发,提出了部分和分解算法的VLSI结构,基于该结构的RTL代码通过了综合和FPGA原型验证,为该算法的后续研究和应用提供了理论基础和实现参考。论文最后给出了PSDA算法的VLSI实现结果:指出了PSDA算法未来的应用前景和发展方向。
相比其它DCT算法,本文提出的PSDA算法实现了以下几个方面的创新和改进。
1.提出了部分和相等的分集准则,通过该准则实现了对频域输出数据的分集,并证明了每一个分集内的元素为时域输入数据部分和的一维DCT变换输出。
2.通过对频域数据进行子集划分,将一个二维DCT变换转换为若干个一维DCT变换,完成DCT变换的乘法运算次数减少了一半。
3.提出了部分和的计算方法和公共加法项的合并原则,通过合并公共加法项减少了加法运算量。
4.传统的DCT算法是针对输入数据长度为2“ 进行计算的,但是在很多应用领域中都要用到长度非2”的DCT算法,而素长度的DCT算法是非2”长度DCT的核心。因此本文在2“长度PSDA算法的基础上提出了改进的二维素长度PSDADCT算法,该算法是基于频域输出数据与部分和的转换和映射关系,将二维素长度DCT变换分解为多个一维素长度DCT变换。同已有的素长度DCT算法相比, 减少了一半的乘法计算量。;
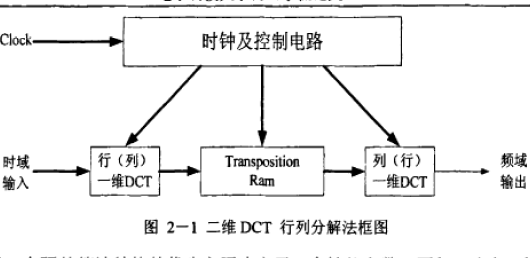
5.提出了基于2”长度PSDA算法的VLSI结构,同间接算法的VLSI结构相比,该结构具有不需要转置变换,处理延时低的优点;同其他直接算法的VLSI结构相比,该结构具有更规则的结构,和更少的乘法器和加法器开销。
6.目前的DCT IP核都是针对2°长度的,并不能满足完全实际应用中的需要。本文在PSDA算法的基础上,分别基于FPGA和ASIC工艺进行了素数长度DCT的IP核设计。仿真和综合结果表明,该设计结构简单、层次清晰,具有高度的规则性和模块性。

声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章





