
资料下载

AD536A中文资料(官方原版)
AD536A是一款RMS到直流转换的整体集成电路,它优于混合式或组合式的电路。AD536A直接计算输入波形的RMS值,包括AC和DC组件。有一个波峰因数补偿表,可以使波峰系数达到7的测量值只有1%的误差。本器件能测量300K带宽大于100mV的信号,误差在3dB范围内。
AD536A商用产品分两个精度级别(A,K)温度范围(0℃ to 70℃)和另一个超范围级别(S)温度范围-55℃ to 125℃。AD536AK有最大±2mV±0.2%的读取误差,而AD536AJ和AD536AS有±5mV±0.5%的最大误差。所有三种都可用14-DIP或10to100脚金属封装。AD536AS也有20脚无铅陶瓷封装。
1,AD536A计算输入的复合AC信号输出等效直流电平。计算信号的rms值比信号电平均值更有用,因为rms反映了信号的功率,还反映了信号的标准偏差。
2、峰值因数是波形的峰值摆动到rms值的比率。峰值因数补偿表可以测量宽动态范围的复杂信号。
3、仅有的外部器件是设定平均周期的电容,它需要专门选定对应电容值。电容值决定了低频率AC信号的精度、纹波和稳定时间。
4、AD536A可使用分离电源供电、单一电源供电,供电电源范围5到36V。1个毫安级的静态电源也可以使用,使其非常适合各式遥控器也可以应用由电池供电的仪表。
5、AD536A可直接替换AD536,提高了带宽和温度漂移标准。
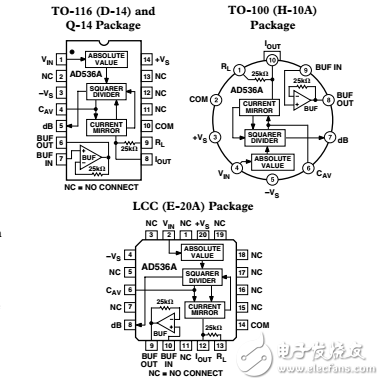
AD536A有一项重要的新功能,能够将rms电平转换成dB值输出。信号rms的对数输出到独立的管脚进行dB转换,其范围有60dB。利用一个外部的参考电流,用户能够很方便地设置0dB电平,能计算输入的任何0.1到2Vrms波形。 AD536A在晶圆级采用激光校准对输入输出补偿,正负波形平衡,7Vrms满量程精度。因此,无需外部调整,即可达到额定精度。
输入输出均有完全保护,输入电平可超出供电电平。输入连接失去供电不会损坏芯片。输出有短路保护。
AD536A
功能:
有效值到直流电平装换 高精度激光微调技术
0.2%最大误差(AD536AX) 0.5%最大误差(AD536AJ) 宽响应能力:
能够计算AC和DC信号的RMS 450KHz带宽:Vrms》100mV 2MHz带宽:Vrms》1V
信号的波峰因数当误差为1%时为7 dB输出有60dB范围 低功耗:1.2mA静态电流 单、双端均可用 整体集成电路
-55℃ to 125℃ (AD536AS)
AD536A的操作原理
AD536A是rms方程的隐性求解,为克服动态范围的rms固有简单计算。AD536A的计算公式如下: Vrms=Avg(V2in/Vrms)
图9是一个AD536A简化的示意图,它被细化为四个注意部分:绝对值电路(整流),乘方/除法器,电流镜像器,缓冲放大器。直流或交流的输入信号Vin可以通过A1、A2转化为一个无极性电流I1。I1驱动一个乘方/除法器的输入,它是一个传递函数: I4=Avg(I21/I4)=I1 rms
电流镜像器也生成输出电流Iout,等于2I4。输出电流Iout可以直接输出,也可以通过R2转换为电压输出,并由A4缓冲来提供低阻抗电压输出。AD536A输出方程如下:
Vout=2R2Irms=Vin rms
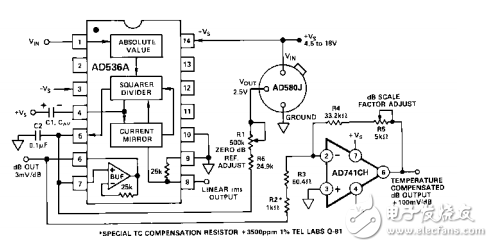
dB输出由Q3的发射极驱动,因为该点的电压是logVin。射极跟随器,Q5,对这个电压进行缓存和偏移,从而当外部输入到Q5发射极电流接近I3时使dB输出电压是0。 dB操作的连接
AD536A附加的信号功率处理能力就是对数或dB输出。内部电路能够准确计算dB工作的范围是60dB。dB测量的连接方式见图10。用户通过调整R1选择0dB电平,以及0dB电流(它设置为在0dB点完全取消了对从乘方/除法器输出的电流取log)…。 频率响应
AD536A利用对数电路进行隐性的rms计算。对于一般的log电路,带宽与信号电平成比例。下图的实线表示了AD536A的输入电平从10mV到7V rms的频率响应。虚线表示高于频率限制1%,10%和3dB的附加读取误差。例如一个1V rms信号会产生小于1%的读取误差频率可达120KHz。一个10mV信号产生1%的读取误差(100uV),器频率只有5KHz。
交流测量精度和波峰因数
在影响交流信号测量准确性的因素中,波峰因数往往被忽视。波峰因数定义为信号峰值幅度与信号rms值得比率。(CF=Vp/Vrms)。常见波形,如正弦波形,三角波形有相对低的波峰因数(<2)。在开关电源和SCR(可控硅)电路中产生的低占空比脉冲串,有很高的波峰因数。比如一个1%占空比的矩形脉冲串,其波峰因数是10(CF=η
1/2
)。图12是AD536A输入1Vrms信号而波峰因数从1
到11时读取误差曲线。用一个rms测量最差的矩形脉冲串(脉冲宽度100us)来进行本测试(所有的能量包含在峰值中)。保持1Vrms输入信号,变化占空比和峰值幅度来产生1到11的波峰因数
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章





