
资料下载

×
如何搞定机器学习中的拉格朗日?看看这个乘子法与KKT条件大招
消耗积分:1 |
格式:rar |
大小:0.4 MB |
2017-12-06
一 前置知识
拉格朗日乘子法是一种寻找多元函数在一组约束下的极值方法,通过引入拉格朗日乘子,可将有m个变量和n个约束条件的最优化问题转化为具有m+n个变量的无约束优化问题。在介绍拉格朗日乘子法之前,先简要的介绍一些前置知识,然后就拉格朗日乘子法谈一下自己的理解。
1.梯度
梯度是一个与方向导数有关的概念,它是一个向量。在二元函数的情形,设函数f(x,y)在平面区域D内具有一阶连续偏导,则对于每一点P(x0,y0)∈D,都可以定义出一个向量:fx(x0,y0)i+fy(x0,y0)j ,称该向量为函数f(x,y)在点P(x0,y0)
的梯度。并记作grad f(x0,y0) 或者∇f(x0,y0),即 grad f(x0,y0) = ∇f(x0,y0) = fx(x0,y0)i+fy(x0,y0)j=(fx(x0,y0),fy(x0,y0)) 。
再来看看梯度和方向导数的关系:如果函数f(x,y)在P(x0,y0)点可微,el = (cosα,cosβ)是与方向L同向的单位向量,则∂f/∂L|(x0,y0) = fx(x0,y0)cosα+fy(x0,y0)cosβ = grad f(x0,y0).el = |grad f(x0,y0)|.cosθ ,其中θ表示的梯度与el 的夹角。由此可知,当θ = 0时,el 与梯度的方向相同时,此时方向导数最大,函数f(x,y)增长最快;当θ = π时,el 与梯度的方向相反时,此时方向导数最小且为负,函数f(x,y)减小最快。
2.等高线(等值线)
通常来说,二元函数 z = f(x,y)在几何上表示一个曲面,这个曲面被平面 z = c(c为常数)所截得的曲线L的方程为:

这是一条空间曲线,这条曲线L在xOy平面上的投影是一条平面曲线L*,它在xOy平面直角坐标系中的方程为:f(x,y) = c 。对于曲线L*上的一切点,已给函数的函数值都是c,所以我们称平面曲线L*为函数z = f(x,y)的等值线(等高线)。再来看看等高线的一些性质:
若fx,fy不同时为零,则等高线 f(x,y) = c上任一点P(x0,y0)处的一个单位法向量为:
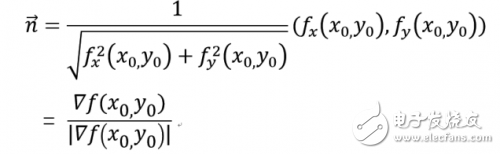
这表明函数f(x,y)在一点(x0,y0)的梯度∇f(x0,y0)的方向就是等高线f(x,y) = c在这点的法向量的方向,而梯度的模|∇f(x0,y0)|就是沿这个法线方向的方向导数∂f/∂n,于是有:

拉格朗日乘子法是一种寻找多元函数在一组约束下的极值方法,通过引入拉格朗日乘子,可将有m个变量和n个约束条件的最优化问题转化为具有m+n个变量的无约束优化问题。在介绍拉格朗日乘子法之前,先简要的介绍一些前置知识,然后就拉格朗日乘子法谈一下自己的理解。
1.梯度
梯度是一个与方向导数有关的概念,它是一个向量。在二元函数的情形,设函数f(x,y)在平面区域D内具有一阶连续偏导,则对于每一点P(x0,y0)∈D,都可以定义出一个向量:fx(x0,y0)i+fy(x0,y0)j ,称该向量为函数f(x,y)在点P(x0,y0)
的梯度。并记作grad f(x0,y0) 或者∇f(x0,y0),即 grad f(x0,y0) = ∇f(x0,y0) = fx(x0,y0)i+fy(x0,y0)j=(fx(x0,y0),fy(x0,y0)) 。
再来看看梯度和方向导数的关系:如果函数f(x,y)在P(x0,y0)点可微,el = (cosα,cosβ)是与方向L同向的单位向量,则∂f/∂L|(x0,y0) = fx(x0,y0)cosα+fy(x0,y0)cosβ = grad f(x0,y0).el = |grad f(x0,y0)|.cosθ ,其中θ表示的梯度与el 的夹角。由此可知,当θ = 0时,el 与梯度的方向相同时,此时方向导数最大,函数f(x,y)增长最快;当θ = π时,el 与梯度的方向相反时,此时方向导数最小且为负,函数f(x,y)减小最快。
2.等高线(等值线)
通常来说,二元函数 z = f(x,y)在几何上表示一个曲面,这个曲面被平面 z = c(c为常数)所截得的曲线L的方程为:

这是一条空间曲线,这条曲线L在xOy平面上的投影是一条平面曲线L*,它在xOy平面直角坐标系中的方程为:f(x,y) = c 。对于曲线L*上的一切点,已给函数的函数值都是c,所以我们称平面曲线L*为函数z = f(x,y)的等值线(等高线)。再来看看等高线的一些性质:
若fx,fy不同时为零,则等高线 f(x,y) = c上任一点P(x0,y0)处的一个单位法向量为:
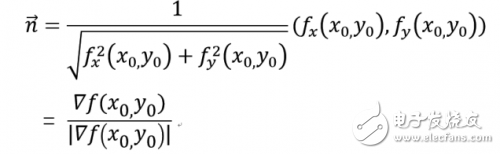
这表明函数f(x,y)在一点(x0,y0)的梯度∇f(x0,y0)的方向就是等高线f(x,y) = c在这点的法向量的方向,而梯度的模|∇f(x0,y0)|就是沿这个法线方向的方向导数∂f/∂n,于是有:

声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
评论(0)
发评论
- 相关下载
- 相关文章
下载排行榜
- 暂无相关数据





