
资料下载

×
陀螺信号去躁方法(Shannon熵和EMD算法)
消耗积分:0 |
格式:rar |
大小:1.10 MB |
2017-11-01
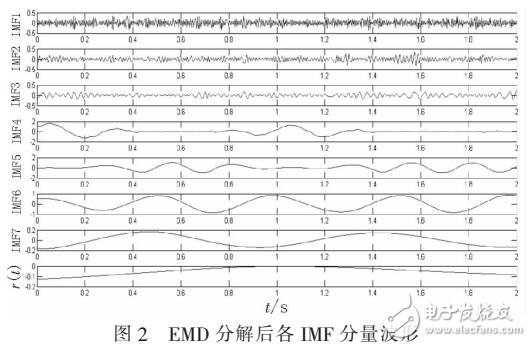
MEMS陀螺仪由于它紧凑的外形、低成本、低功耗而被大量应用于防御、汽车、航空航天等各个领域。也正因为陀螺仪的小型化和高制作精度,导致它对于电子和机械的噪声相当敏感,输出的数据中带有较大的随机漂移,而这些漂移量是非线性、非稳定的,使得测量数据中存在较大误差。
常用的陀螺仪信号降噪方法有卡尔曼滤波、短时傅里叶变换、小波变换等。其中,卡尔曼滤波是基于建立线性模型,然而线性模型对于非稳定、非线性漂移信号并不是很有效。短时傅里叶变换应用于频域内可以获得较高的分辨率,在时域范围分辨率则较低:小波变换虽然在时频域内分辨率较高,但是在处理信号时先确定基函数和分解尺度,那么滤波结果也将是固定尺度,这样的非白适应方法在处理漂移信号时也没有较好的成效。由于受傅里叶变换的束缚,在信号的边界还会发生频谱泄露。而EMD (Empirical Mode Decomposition, EMD)算法不仅可以较好的分析信号的频率成分,分辨率也很高;在边界也不会发生频率混叠现象,适合处理非线性、非平稳信号。本文提出了基于Shannon熵和EMD算法,对陀螺仪信号进行去噪处理的方法。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
评论(0)
发评论
- 相关下载
- 相关文章





