
资料下载

×
基于超完备字典的压缩感知电能质量数据重构
消耗积分:1 |
格式:rar |
大小:1.39 MB |
2018-04-23
传统电能质量海量数据处理均基于Nyquist采样定理。在数据压缩过程中,通常还需消除大量的采样冗余数据,从而造成了采样资源的严重浪费。利用压缩感知(Compressed Sensing,CS)理论对原始信号进行压缩采样,得到少量的测量信号,便能恢复重构出原始信号,从而大大缓解了存储空间的压力,具有广阔的应用前景。
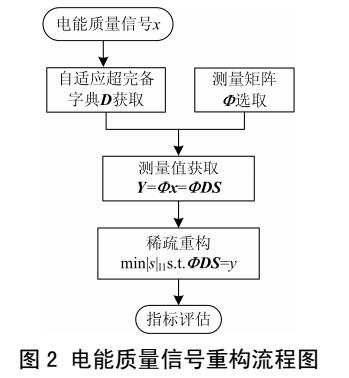
应用CS理论的前提是信号具有稀疏性。在压缩感知的稀疏表示部分,经典的稀疏化的方法有离散余弦变换(DCT)、傅里叶变换(FFT)、离散小波变换(DWT)等。而且其对应的基函数是固定的,因此不能根据数据本身的特点进行自适应调整。采用短时傅里叶变换对于局部特征的捕捉性能不是很好;采用小波变换没有方向识别能力。电能质量信号包括电压脉冲、振荡、暂降和暂升等,用于传统稀疏表示的普通正交基函数并不能自适应地获得最佳稀疏表示。因此,本文提出了将压缩感知与字典学习相结合的新思路,得到最佳的电能质量数据稀疏表达方式,从而实现了电能质量数据的重构。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
评论(0)
发评论
- 相关下载
- 相关文章




