
资料下载

压缩感知的理论框架和应用的系统概述和信号重构算法研究
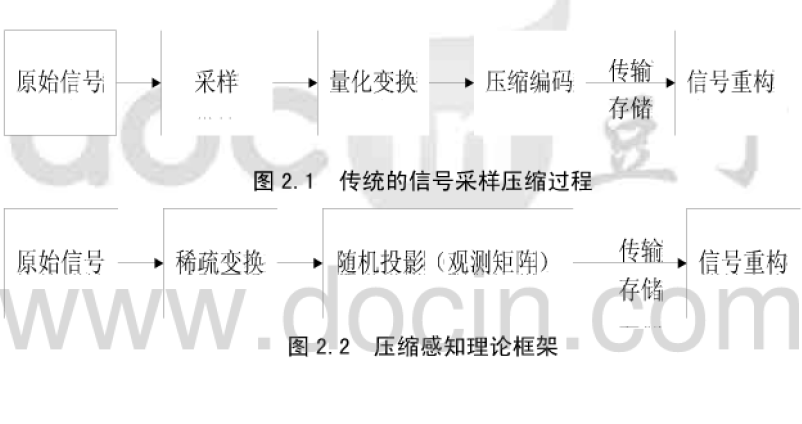
本文对压缩感知理论的理论框架和应用进行了系统概述。该理论针对稀疏信号,在对信号进行采样的同时完成数据压缩,从而大量节约了计算资源、存储资源和传输资源。它包括信号的稀疏变换、观测矩阵的设计和信号的重构三个方面的内容。这里将重点放在最为关键的信号重构方面。接下来对重构算法中的正交匹配追踪算法和梯度投影算法的实现原理,算法结构等进行具体的研究并做出信号仿真结果。最后,在正交匹配追踪算法的基础上,提出了一种改进方案。针对原有算法的重构速度比较慢和迭代次数需要给定的问题,利用最优正交匹配算法中的匹配原子的选择准则和后向投影思想进行迭代重构。分别应用一维信号和二维图像进行重构仿真,将得到的实验结果和原有算法的仿真结果对比,可以看出优化后的算法在降低采样点数要求的同时,能够比较精确的重构信号,算法性能得到提升。

众所周知,传统的信号处理框架的基础是傅立叶变换,手段是频谱分析,准则为奈奎斯特采样定理,这是几乎所有的视听消费电子、医疗影像设备、收音机接收器、雷达通讯等系统所必须遵循的金科玉律。根据奈奎斯特采样定理的规定:信号的采样频率不得低于信号带宽的2倍,否则就会出现信息的丢失。因此在宽带模拟数字化过程中往往需要非常高的采样率,同时又要针对获取的大量原始采样信息进行数据压缩和传输,这就对存储资源、传输资源和计算资源都造成了极大程度的浪费。同时,由于在实际应用中电子器件(如A/D转换器等)的物理性约束问题,提高采样频率的代价极其巨大。另一方面,随着现代信息技术的高速发展和人们对信息数据量的需求的不断增加,对传统的信号处理框架要求的采样和处理速度都提出了更高的要求,于是我们提出个新问题:能否建立-一个新的信号处理框架,在保证信息没有损失的同时用远低于奈奎斯特采样定理所要求的采样速率对信号进行采样,并且能够精确的恢复信号?假如这个问题得到解决,就可以显著的减小数据处理、传输和存储的代价,进步降低信号处理的时间成本和器件成本。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章




