
资料下载

国际机器人技术研究杂志机械手的自适应控制
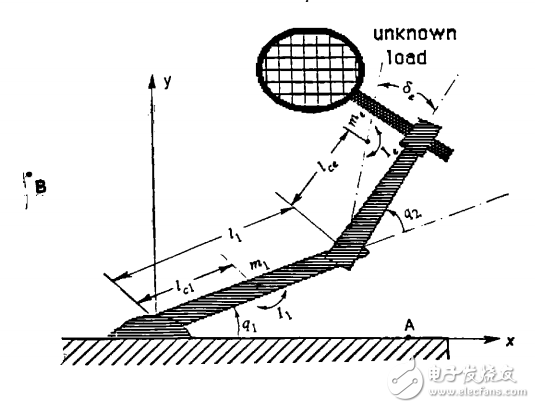
Adaptive control, as a branch of systems theory, is not yet quite mature (see, for instance, Astr6m 1983; 1984)。 Yet, the practically motivated drive to make robot manipulators capable of handling large loads in the presence of uncertainty on the mass properties of the load or its exact position in the end-effector, as well as the old &dquo;cybernetic&dquo; ideal of developing learning capabilities in machines, has spurred much research on adaptive control of robot manipulators (see, e.g., Hsia 1986, for a recent review)。 The nonlinearity of robot dynamics, however, makes them even more complex to analyze than the linear dynamic systems on which most of the existing adaptive control theory has been traditionally focused. Several approaches have been considered. Some choose to ignore the dynamic complexity and fit the measured data to a second-order, linear, time-varying model, using for instance a recursive least-squares approach (see, e.g., Koivo 1986)。 Others do exploit the known structure of the system dynamics (e.g., Khosla and Kanade 1985; Atkeson et al. 1985; Craig et al. 1986), although they generally require estimation of joint accelerations. Another class of algorithms considers the &dquo;learning&dquo; of specific tasks through the use of feedforward signals (Arimoto et al. 1985; Atkeson et al. 1986), without explicitly updating the manipulator model itself.
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章






