
资料下载

飞行器姿态角解算的全角度双欧法
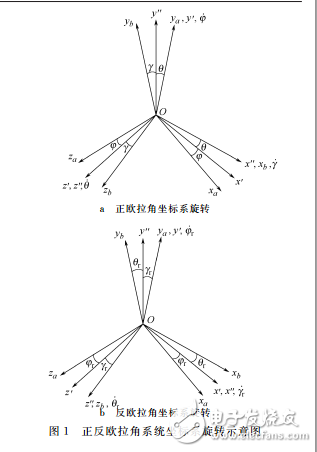
在飞行力学研究中,飞行器姿态通常采用欧拉角来描述。欧拉角是通过求解欧拉方程得到的, 但是欧拉方程存在奇异性,当俯仰角为+π/2时, 滚转角和偏航角无法定值,同时临近该奇点的区域求解误差过大,导致求解失真。为了避免这个问题,最初人们采用限制俯仰角取值范围的方法,严重限制了大机动飞行的姿态模拟。为了克服这个问题,文献[1]提出了双欧法,该方法的思想是用两套不同的欧拉角描述同一个姿态,在不同的角度范围内采用不同的欧拉角描述,利用正反欧拉 角奇异性的倒挂关系,以二者解算准确的精华区进行分区接替运算。这种方法彻底克服了传统单欧法的奇异性,同时获得了很高的计算精度。该方法受 到 了 广 泛 关 注[2-3],并 在 实 践 中 得 到 了 应用[1]。但是传统双欧法限定俯仰角的取值范围为 [-π/2,+π/2],视超出该范围的姿态角为“奇观值”,尽管在过去大多数情况下,该取值范围可以满足要求,但是随着航空航天技术的发展,超机动飞行动作开始在飞行器使用中出现,例如著名的 SU27战斗机“普加乔夫机动”(也称为“眼镜蛇机动”),其俯仰角就越过90°达到110°,实现了名副其实的“倒飞”。另外,现代舰载防空导弹的垂直发射系统也超过了传统双欧法的俯仰角取值范围。 传统双欧法的正反欧角度转换方法使得该方法无法连续模拟越过±90°俯仰角的超机动飞行,这对于超出±90°的连续数值积分模拟是不利的。 本文对传统双欧法的正反欧角度转换方法进行了改进,使得欧拉角在数值模拟过程中能始终保持连续性,从而能适应全角度的姿态角数值求解.
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章






