
资料下载

使用Seeeduino Wio终端模拟Dadiplus掷骰子
描述
想象一下掷硬币九次,连续九次得到“正面”。第 10 次掷出“反面”的概率是多少?
如果您回答“90%”,那么请继续阅读,当然欢迎您稍微回顾一下统计数据。
If, on the other hand, you are among those elected who answer (correctly) "50%", then you already know the difference between dependent and independent events. 正如在统计领域中所重复的那样,一枚硬币对其过去没有记忆,每次抛硬币正面朝上的概率等于反面朝上的概率。虽然之前的系列看到连续释放了 99 个“反面”,但每次我们将硬币抛向空中,与概率相关的数字都会重置,我们从头开始。
显然,对于那些像普通人一样习惯于在所有感官知觉中寻找模式的人来说,这种行为至少是违反直觉的。我们面临着一个通常的、非常古老的故事,它把我们看作是演员,通过试图识别每一个现实表现背后的根本原因来寻求改善我们的状态。
从硬币到骰子
如果我们正好有 50% 的机会看到硬币正面朝上或反面朝上(忽略硬币站在边缘的那些罕见的例外情况),骰子的每一面出现的几率是多少?很简单:每次滚动,每张脸都有六分之一的机会出现。所以,大约 16.67%。
换句话说,从 1 到 6 的每个值都具有完全相同的退出概率(除非你已经密封了骰子……)。
当我们增加掷骰子的数量时,事情会变得更有趣:无论如何,实际上用两个骰子获得值 1 是不可能的(显然……)。在下表中,我们可以看到有多少种不同的方法可以获得每个值作为结果。
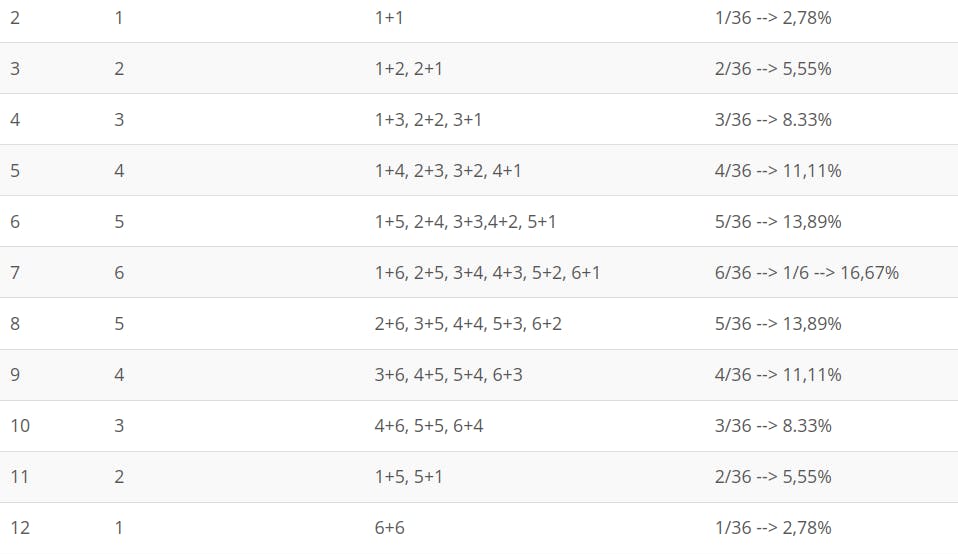
用一点组合数学(但也只是常识)很容易认识到每个数字的输出可能性不再相同,因为某些值可以以几种不同的方式组合。如果我们看一下表格,我们会发现每次投掷都有 36 种不同的可能组合。值 2 和值 12 在每次掷骰时都有 36 分之一的机会出现,值 3 和值 11 在每次掷骰时各有 2 次退出的概率,依此类推。换句话说,对于单个骰子,每个数字出来的概率不再相同,特别是两个骰子出现2或12的概率等于出一个正数在轮盘赌中。(如果我们暂时不考虑零,则为 1/36 或 2.78%)。
让我们增加复杂性。
如果我们使用两个以上的骰子会发生什么?每个版本的几率是多少?他们会保持增长的明显线性,还是会创造出奇怪的曲线?我们可以手动计算这些值,但随着计算量的增加,我们会冒犯错误的风险。另一方面,计算机会非常轻松......
我们有一个具有特殊计算能力的小板,即Seeeduino Wio 终端。这是一个 Arduino 类固醇,配备SAMD51系统和ARM Cortex M4 处理器。只需编写一个简单的程序,使用 random() 函数模拟掷 6 个骰子,将每个组合的输出值累加并计算总输出的百分比。
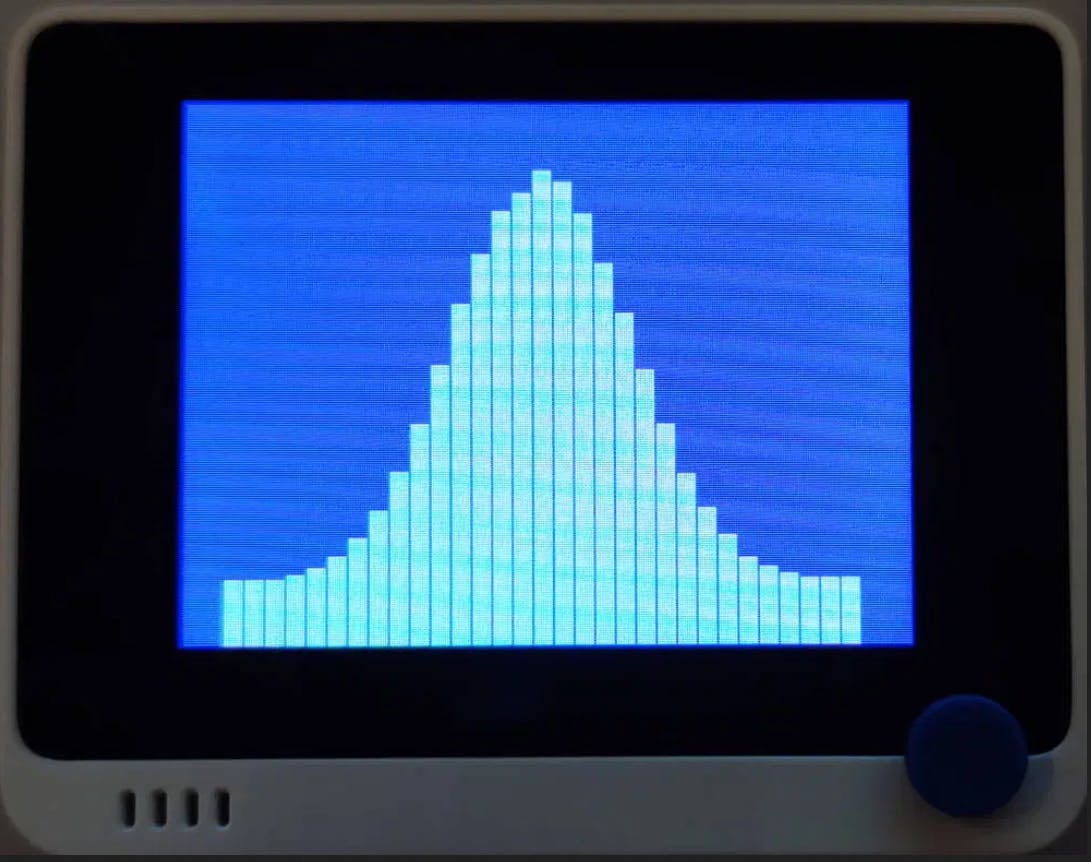
为了使程序更有趣,我们将在表格中添加每个组合的输出数量显示。
在程序结束时,只需单击蓝色按钮即可获得为每个组合计算的概率值列表。
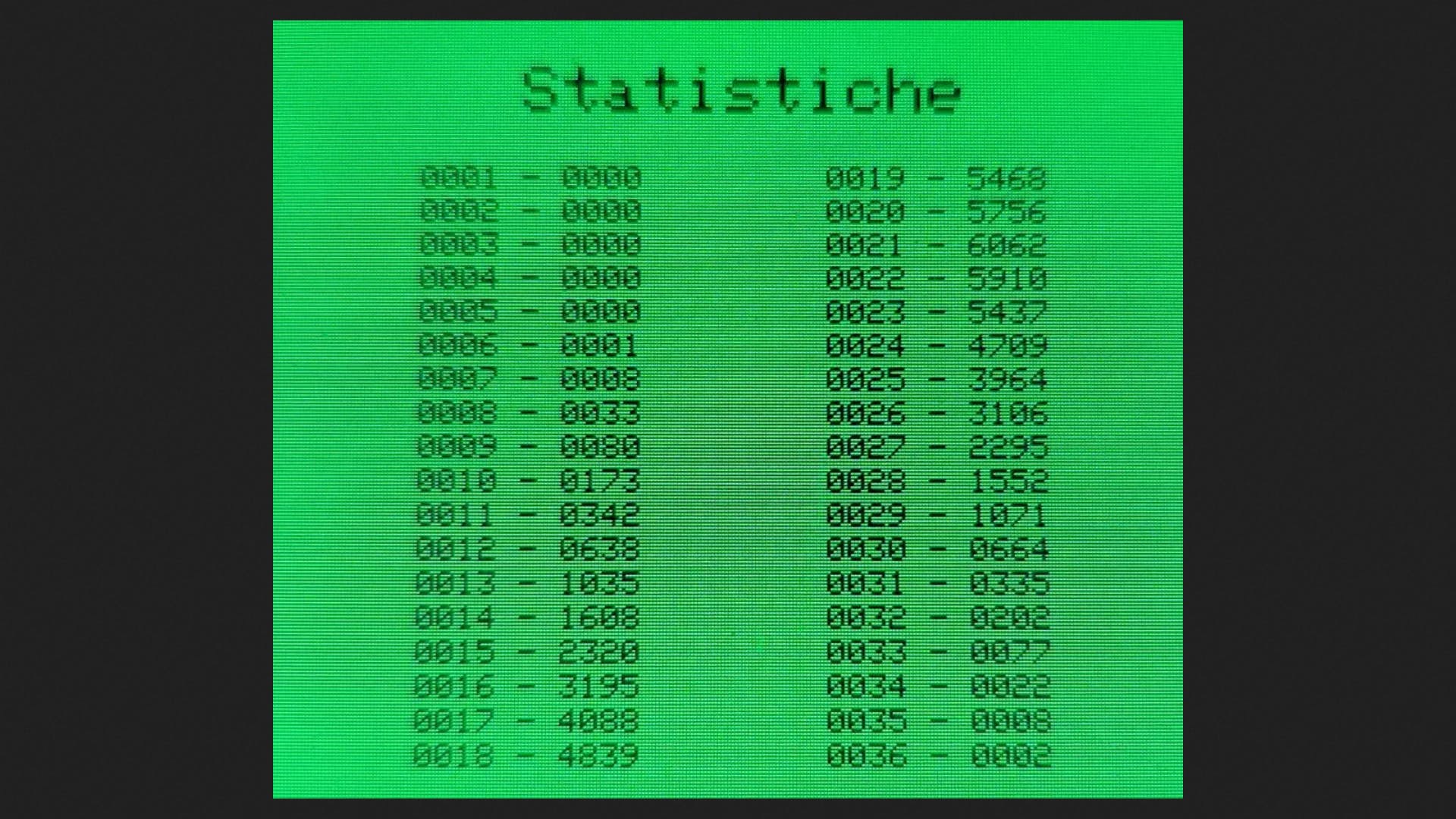
该程序可在GitHub和附件部分获取。
如果您需要澄清,请随时与我联系。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章





