
资料下载

用于定位的实用卡尔曼滤波器
描述
*免责声明*
我不是卡尔曼滤波器专家。只是分享我的故事。也许它对某人有帮助。如果您有任何建议或想法,请随时在评论中留下它们。
使用卡尔曼滤波器进行定位?
我做了一个在户外导航的机器人。它使用航路点进行导航。为此,它需要知道它在哪里。这就是大问题开始的地方。知道某事是,并不容易。GPS 看起来很明显,但并不精确。这是因为您需要移动才能获得不错的定位。当附近有树木和房屋等大物体时,您会得到一种称为“多路径”的东西。
使用 IMU?大多数小型 IMU 不是很一致。您并不总是获得相同的速度读数。在毛茸茸的地形(草)上,情况更糟。
卡尔曼滤波器?卡尔曼滤波器可以做一些叫做“传感器融合”的事情。它将多个传感器的输出组合成一个一致的输出。
卡尔曼滤波器
卡尔曼滤波器可用作滤波器/平滑器或传感器融合算法。
卡尔曼滤波器似乎在互联网上有很好的记录。但他们不是。
问题是; 大多数好的解释都停留在理论上。他们无法解释某件事在实践中的含义。
卡尔曼滤波器的基础知识
卡尔曼滤波器适用于概率。“系统”/机器人的当前“状态”/位置可能位于何处。
机器人当前位置的可能位置。
系统当前状态的可能情况。
可能的引擎盖由“正态分布”表示。
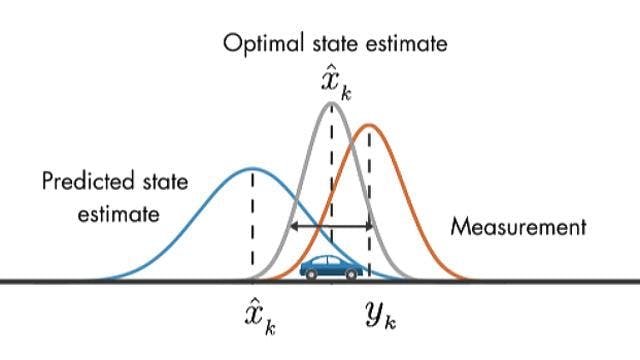
这个可能的引擎盖可以与谷歌地图的位置圈进行比较。“你很可能在这个蓝色圆圈内。”
网上有一些很好的解释。这一个说明了这一点。https://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/
让我们变得实用
在编程(Python)中是定义在矩阵中的卡尔曼滤波器。这些矩阵包含卡尔曼滤波器的配置。
有以下矩阵:
- X:状态(输出)
- P:状态噪声
- F:状态转换模型
- U:预测输入
- B:输入模型
- Q:过程噪音
- Z:更新测量值(输入)
- H:观察模型
- R:观察噪声
我使用这个 Python 类进行计算。(作为 np导入的 Numpy )
import numpy as np
class KalmanFilter(object):
def __init__(self, F = None, B = None, H = None, Q = None
, R = None, P = None, x0 = None):
if(F is None or H is None):
raise ValueError("Set proper system dynamics.")
self.n = F.shape[1]
self.m = H.shape[1]
self.F = F
self.H = H
self.B = 0 if B is None else B
self.Q = np.eye(self.n) if Q is None else Q
self.R = np.eye(self.n) if R is None else R
self.P = np.eye(self.n) if P is None else P
self.x = np.zeros((self.n, 1)) if x0 is None else x0
def predict(self, u=0):
self.x = np.dot(self.F, self.x) + np.dot(self.B, u)
self.P = np.dot(np.dot(self.F, self.P), self.F.T) + self.Q
return self.x
def update(self, z):
y = z - np.dot(self.H, self.x)
S = self.R + np.dot(self.H, np.dot(self.P, self.H.T))
K = np.dot(np.dot(self.P, self.H.T), np.linalg.inv(S))
self.x = self.x + np.dot(K, y)
I = np.eye(self.n)
self.P = np.dot(np.dot(I - np.dot(K, self.H), self.P)
, (I - np.dot(K, self.H)).T) + np.dot(np.dot(K, self.R)
, K.T)
你想要什么&你有什么?
要开始配置矩阵,您需要问自己两个问题。
- 你想要什么?卡尔曼滤波器必须给出什么输出?就我而言,我需要知道机器人的位置。
- 你有什么?卡尔曼滤波器有哪些输入数据?这可以是 GPS 位置、IMU 加速度……您的输入数据比您想象的要多!大多数 GPS 模块提供方位和速度。尝试从传感器中获取所有数据。
X 矩阵
x 矩阵是卡尔曼滤波器的输出。如果要预测位置,则填写 XYZ 位置。
Xpos
Ypos
零点
知道速度对于计算位置很方便。所以我填写了XYZ速度。
速度
速度
速度
X矩阵的最终结果是:
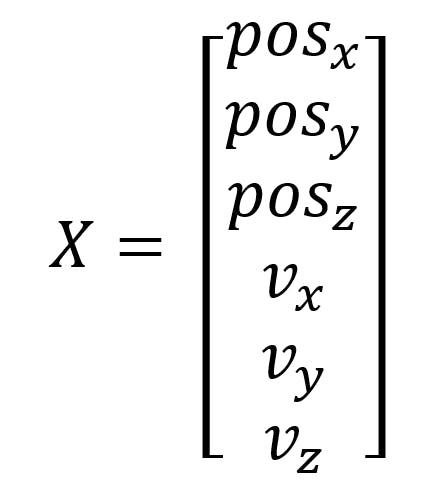
输入:U 矩阵和 Z 矩阵
有 2 个输入。状态预测的 U 矩阵。状态更新的 Z 矩阵。
当您运行卡尔曼滤波器时,您首先要进行预测。做出预测后,您可以做 2 件事:进行另一个预测或更新模型。
- IMU 的读取频率为 100Hz。
- GPS 的读取频率为 20Hz。
我使用 IMU 作为状态预测(U 矩阵)的输入。用于状态更新的较低频率 GPS。您的卡尔曼滤波器可以做出比更新更多的预测。这就是为什么您将高读取频率输入作为状态预测输入。
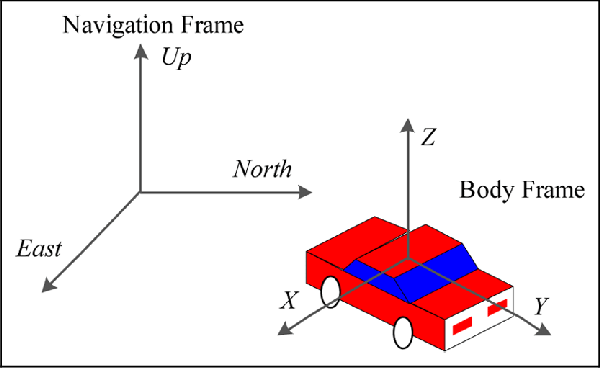
框架
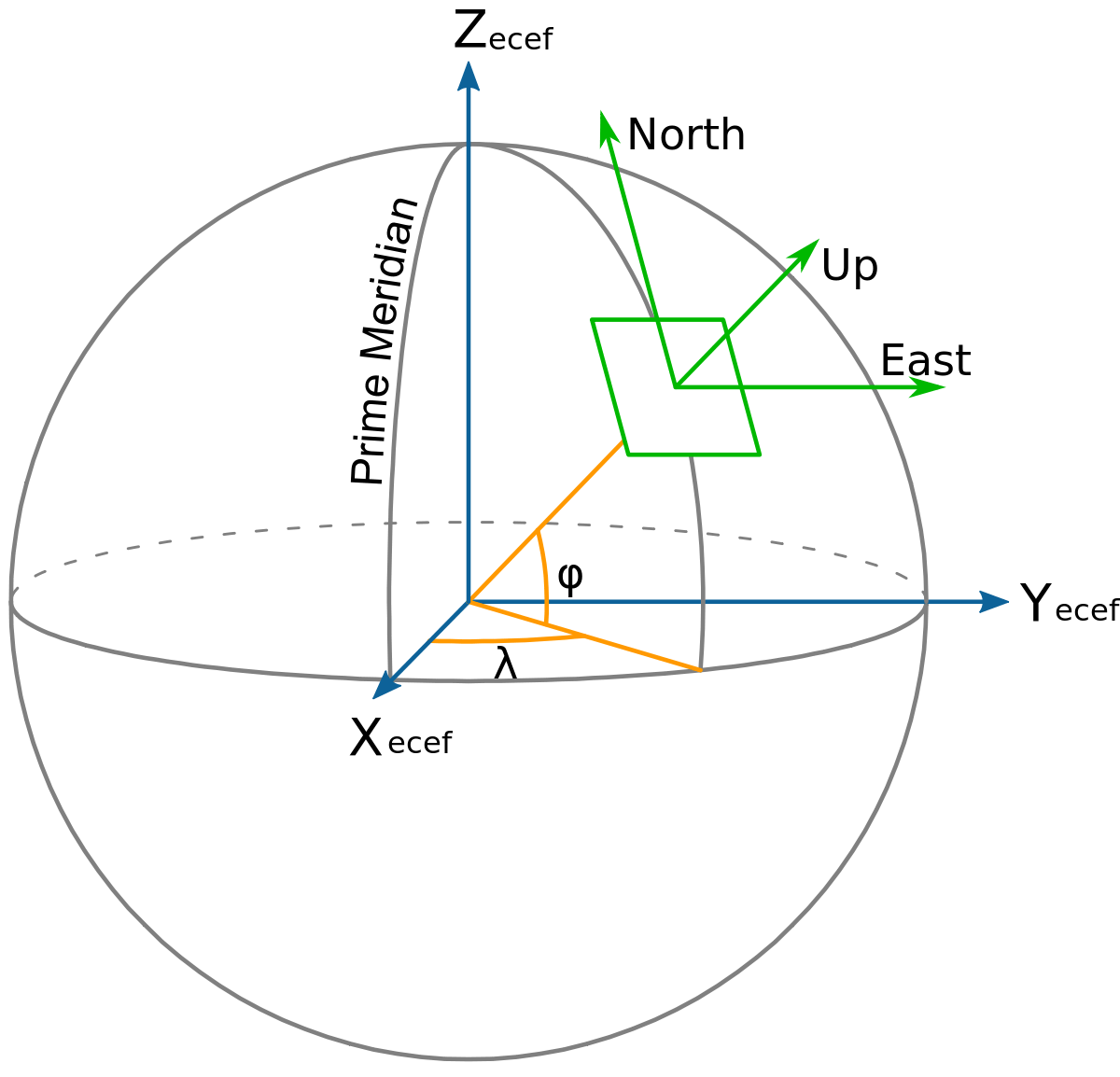
在我们开始向卡尔曼滤波器提供数据之前。我们必须首先正确格式化数据。加速度必须转换为正确的框架和正确的比例。有 3 帧。
- GPS全球框架;经度和纬度
- 局部定位框架;卡尔曼滤波器工作的局部坐标系。它有一个参考点(基站)和一个方向(北)。
- 车身框架;IMU 工作所在的框架。它是机器人相对于本地框架的方向。
import math
def GPS_velocity_to_local(gpsVel, angle):
vel = gpsVel
Vx = math.cos(angle) * vel / 3.6 # 3.6 for km/h to m/s
Vy = math.sin(angle) * vel / 3.6 # 3.6 for km/h to m/s
v = [Vx, Vy, 0]
return v
def GPS_position_to_local(gpsRefPosition, gpsCurrentPosition):
lon1 = gpsRefPosition[0]
lat1 = gpsRefPosition[1]
lon2 = gpsCurrentPosition[0]
lat2 = gpsCurrentPosition[1]
dx = (lon1 - lon2) * 40000 * math.cos((lat1 + lat2) * math.pi / 360) / 360 * 1000
dy = (lat1 - lat2) * 40000 / 360 * 1000
return [dx, dy]
import numpy as np
import math
def IMU_acceleration_to_local(bodyRotation, acceleration):
eulXYZ = bodyRotation
y = eulXYZ[0] #yaw
p = eulXYZ[1] #pitch
r = eulXYZ[2] #roll
mes = np.array([
[acceleration[0]],
[acceleration[1]],
[acceleration[2]]
])
c = math.cos
s = math.sin
# Direction cosine matrix
trans = np.array([
[
[c(y)*c(p), c(p) * s(y), -s(p)],
[c(y)*s(p)*s(r)-c(r)*s(y), c(y)*c(r)+s(y)*s(r), c(p)*s(r)],
[c(y)*c(r)*s(p)+s(y)*s(r), c(r)*s(y)*s(p)-c(y)*s(r), c(p)*c(r)]
]
])
out = np.dot(trans, mes).tolist()[0]
out = [out[0][0]*-1, out[1][0]*-1, out[2][0]]
return out
U 矩阵
U 矩阵是卡尔曼滤波器的主要输入矩阵。它用于状态预测。在 U 矩阵中,最好使用您的高读取频率输入数据。就我而言:IMU 数据。该矩阵不是必需的。如果您没有第二个传感器。
IMU 以 m/s 为单位提供加速度。我们可以使用这个加速度来更新位置和速度。
在我们可以使用加速之前。我们需要从身体框架转换到局部框架。我们可以使用 IMU 的绝对方向。通过使用方向余弦矩阵,我们可以转换两帧之间的加速度。
我们的 U 矩阵将如下所示:
斧头
哎
阿兹
0
0
0
Ax、Ay 和 Az 是转换到局部坐标系的 XYZ 加速度。3 个零是我们不使用的附加输入。我稍后会回来。
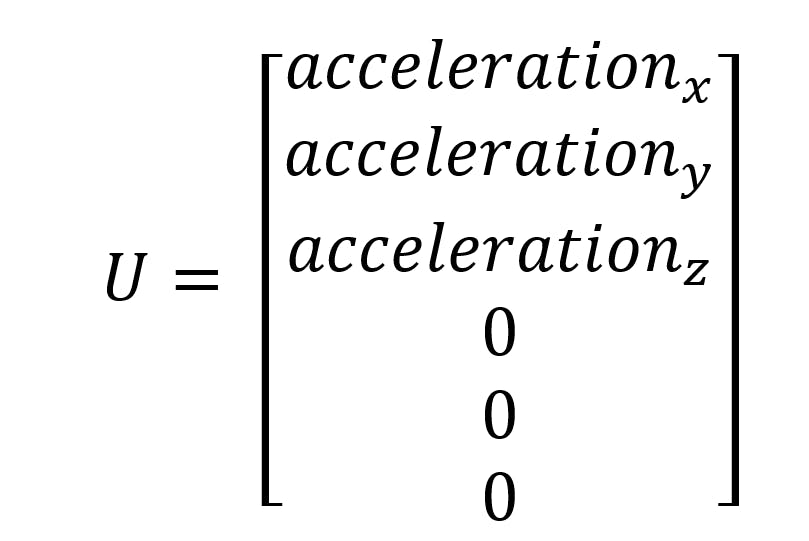
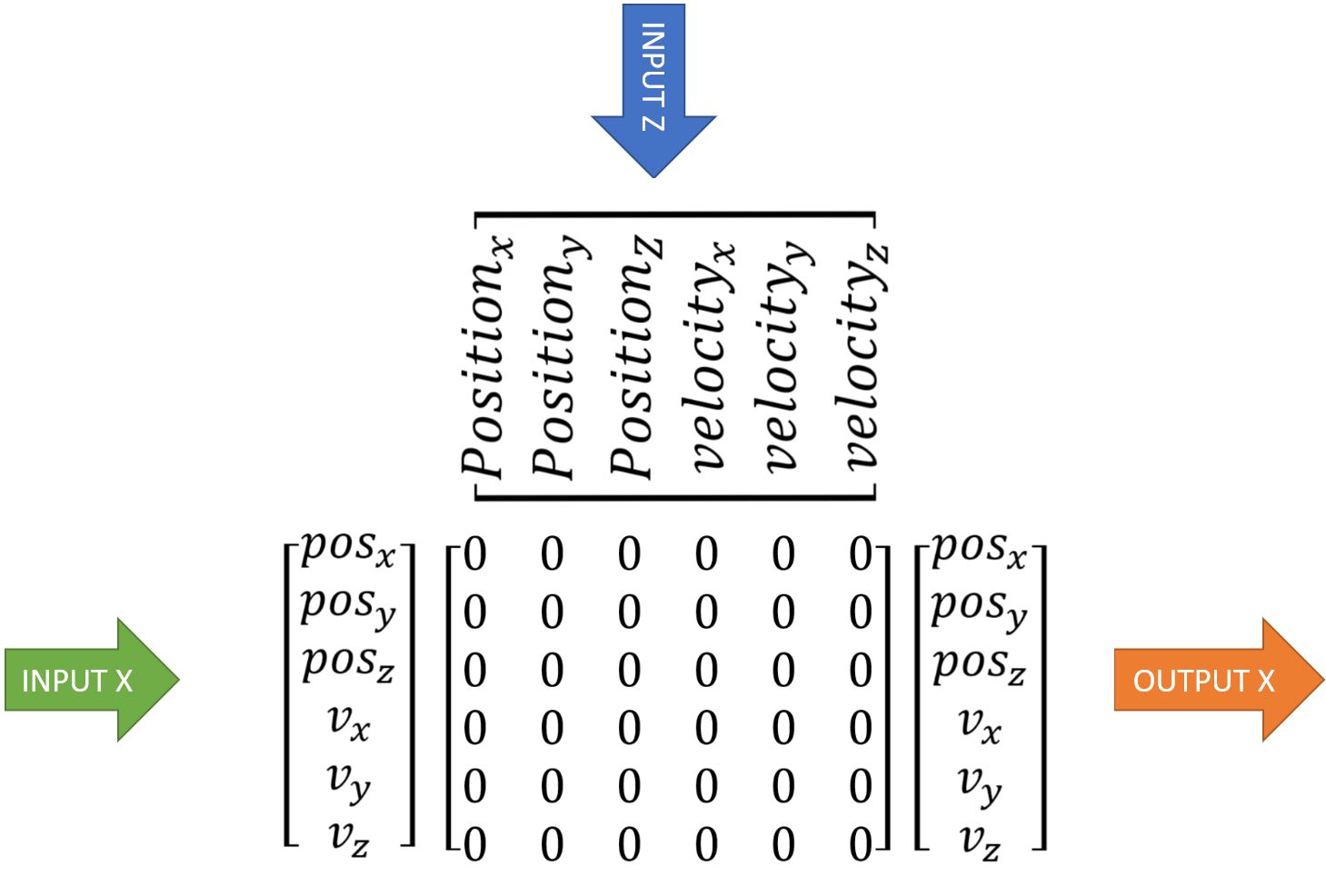
B矩阵
B 矩阵包含输入 (U) 和输出 (X) 之间的关系。它告诉卡尔曼滤波器 U 矩阵如何影响状态(X 矩阵/输出)。

在左边,我们有之前的状态(X 矩阵)。在中间,我们有 B 矩阵。在顶部,我们有输入 U 矩阵。在右边,我们有未来状态(输出/X 矩阵)。我们希望通过我们的测量(U 矩阵/输入)来影响未来的状态/输出。
加速度与位置之间的关系是加速度的二阶导数。
deltaTime²/2

速度和加速度之间的关系是增量时间。

最终结果将是:

Q矩阵
Q 矩阵包含来自 U 矩阵的输入的方差。它包含您输入的常见错误。一个非常小的数字意味着您的传感器/输入精度很高。高数字意味着您的输入非常不准确。除非未使用,否则不要使用 0。
您在矩阵的对角线上填写输入的方差。
查找输入的方差。可以从传感器的数据表中获得传感器的方差。但是,大多数时候这是错误的。还有另外两种获得方差的方法。
- 在系统正常运行时测量传感器读数。然后同时用更好的传感器进行测量以进行比较。这种方式不太实用。除非您用来比较的测量值非常精确。
- 在系统空闲/不移动时测量传感器读数。并将传感器读数与 0 进行比较。这会给您带来差异。不是最好的。
Q 矩阵可以如下所示:

Z矩阵
Z矩阵是第二个输入矩阵。它用于状态更新。通常你把你的低读取频率传感器日期放在这里。
Z 矩阵包含 GPS 测量值。GPS 提供定位经度和纬度。long 和 lat 被转换为 XYZ 坐标中的局部坐标系(以米为单位)。GPS还提供速度。这些是相对于北的,以公里/小时为单位。我们将速度转换为 m/s。Z 矩阵将如下所示:
位置X
位置Y
位置Z
速度X
速度Y
速度Z

H矩阵
H 矩阵类似于 B 矩阵。它包含 Z 矩阵输入和输出(X 矩阵)之间的关系。填充 H 矩阵与填充 B 矩阵的过程相同。
在这种情况下,GPS 输入与输出(X 矩阵)具有 1 对 1 的关系。H矩阵是单位矩阵。

R矩阵
R 矩阵包含来自 Z 矩阵的输入的方差。您仅使用对角线来输入方差。可以以与 Q 矩阵的方差相同的方式得出方差。
我在机器人静止时测量了 GPS 的偏差。这将为您提供 GPS 的变化。就我而言,R 矩阵如下所示:

F矩阵
F 矩阵包含数据从状态到状态的关系。例如,速度通过增量时间影响位置。
我们想要我们未来状态的当前位置和速度。我们希望速度通过增量时间影响位置。为了将当前状态传播到未来状态,我们将从一个统一矩阵开始。

现在我们希望速度通过增量时间影响位置。

P矩阵
P 矩阵包含当前状态的方差(X 矩阵)。卡尔曼滤波器将自行更新值。您可以将其初始化为单位矩阵。或者,您可以使用之前运行的 P 矩阵。当您使用上一次运行的 P 矩阵时。卡尔曼滤波器在开始时会更准确。

补充说明
- 卡尔曼滤波器第一次可能不起作用。这是因为方差在现实世界中不是恒定的。传感器的方差是不断变化的。GPS模块在机器人移动时更加准确。当机器人空闲时,加速度为零。这是非常精确的。因为我们知道机器人何时移动。您知道您的电机何时通电。
- 优化卡尔曼滤波器非常重要。必须在过滤器运行时调整方差。
- 协方差矩阵(Q 和 R)之间的比率比数字更重要。
- 当您知道输入错误时覆盖输入是个好主意。如果您知道实数,覆盖它可能会有所帮助。
结论
卡尔曼滤波器是过滤噪声和组合传感器的好算法。但是,它有其局限性。这不是魔术。如果您的传感器数据是垃圾,卡尔曼滤波器的结果也不会好很多。IMU的不一致是个大问题。GPS模块的多路径是一个问题。有些是可以解决的。您可以使用更多高质量的传感器。但它变得非常迅速。
在我的项目中。卡尔曼滤波器改进了定位。但我从来没有让它按我的意愿工作。获得低于 1 米的精度很难。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。 举报投诉
- 相关下载
- 相关文章








